Алгебраические выражения в математике: определение, примеры решения и свойства

Алгебраические выражения

Содержание:

Алгебраические выражения. Основные понятия

Алгебраические выражения — это одна или несколько алгебраических величин (чисел и переменных), связанных между собой знаками арифметических операций: сложения, вычитания, умножения и деления, а также извлечения корня и возведения в степень (причём показатели корня и степени должны обязательно быть целыми числами) и знаками последовательности применения этих операций (обычно скобками различного вида). Количество величин, входящих в алгебраическое выражение, должно быть конечным.

Виды алгебраических выражений

Из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, возведения в рациональную степень и извлечения корня и с помощью скобок составляют алгебраические выражения.

Примеры алгебраических выражений:

Если алгебраическое выражение не содержит деления на переменные и извлечения корня из переменных (в частности, возведения в степень с дробным показателем), то его называют целым выражением. Из написанных выше целыми являются выражения 1), 2) и 6).

Если алгебраическое выражение составлено из чисел и переменных с помощью действий сложения, вычитания, умножения, возведения в степень с натуральным показателем и деления, причем используется деление на выражения с переменными, то его называют дробным выражением. Так, из написанных выше дробными являются выражения 3) и 4).

Целые и дробные выражения называют рациональными выражениями. Так, из написанных выше рациональными являются выражения 1), 2), 3), 4) и 6).

Если в алгебраическом выражении используется извлечение корня из переменных (или возведение переменных в дробную степень), то его называют иррациональным выражением. Так, из написанных выше иррациональными являются выражения 5) и 7).

Итак, алгебраические выражения могут быть рациональными и иррациональными. Рациональные выражения, в свою очередь, разделяются на целые и дробные.

Допустимые значения переменных. Область определения алгебраического выражения

Значения переменных, при которых алгебраическое выражение имеет смысл, называют допустимыми значениями переменных. Множество всех допустимых значений переменных называют областью определения алгебраического выражения (или областью допустимых значений переменных — ОДЗ).

Целое выражение имеет смысл при любых значениях входящих в него переменных. Так, при любых значениях переменных имеют смысл целые выражения 1), 2), 6) из п. 48.

Дробные выражения не имеют смысла при тех значениях переменных, которые обращают знаменатель в нуль. Так, дробное выражение 3) из п. 48 имеет смысл при всех , кроме = 1, а дробное выражение 4) имеет смысл при всех кроме значений

Иррациональное выражение не имеет смысла при тех значениях переменных, которые обращают в отрицательное число выражение, содержащееся под знаком корня четной степени или под знаком возведения в дробную степень. Так, иррациональное выражение 5) имеет смысл только при тех при которых а иррациональное выражение 7) имеет смысл только при (см. п. 48).

Если в алгебраическом выражении переменным придать допустимые значения, то получится числовое выражение; его значение называют значением алгебраического выражения при выбранных значениях переменных.

Пример:

Найти значение выражения

Решение:

Имеем

Понятие тождественного преобразования выражения. Тождество

Рассмотрим два выражения

При х = 2 имеем Числа 0 и 3 называют соответственными значениями выражений при х = 2. Найдем соответственные значения тех же выражений при х = 1:

Соответственные значения двух выражений могут быть равными друг другу (так, в рассмотренном примере выполняется равенство), а могут и отличаться друг от друга (так, в рассмотренном примере ).

Если соответственные значения двух выражений, содержащих одни и те же переменные, совпадают при всех допустимых значениях переменных, то выражения называют тождественно равными.

Тождеством называют равенство, верное при всех допустимых значениях входящих в него переменных.

Так, тождественно равны выражения

Пропорция (см. п. 30) есть тождество при всех значениях , кроме = 1, поскольку при = 1 знаменатели дробей обращаются в нуль, т. е. дроби не будут иметь смысла.

Замена выражения выражением (сократили на с) есть тождественное преобразование выражения при ограничениях Значит, = — тождество при всех значениях переменных, кроме Ь = 0, с = 0. Верные числовые равенства также называют тождествами.

Замену одного выражения другим, тождественно равным ему, называют тождественным преобразованием выражения.

Эта лекция взята со страницы полного курса лекций по изучению предмета “Математика”:

Смотрите также дополнительные лекции по предмету “Математика”:

Присылайте задания в любое время дня и ночи в whatsapp.

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Алгебраические выражения

Средняя оценка: 4.4

Всего получено оценок: 749.

Средняя оценка: 4.4

Всего получено оценок: 749.

Алгебраические выражения начинают изучать в 7 классе. Они обладают рядом свойств и используются в решении задач. Изучим эту тему подробнее и рассмотрим примеры решения задачи.

Определение понятия

Какие выражения называют алгебраическими? Это математическая запись, составленная из чисел, букв и знаков арифметических действий. Наличие букв – это основное отличие числовых от алгебраических выражений. Примеры:

4а + 5;
6b – 8;
5с : 6 * (8 +5 ).

Буква в алгебраических выражений обозначает какое-либо число. Поэтому она называется переменной – в первом примере это буква а, во втором – b, а в третьем – с. Само алгебраическое выражение еще называют выражением с переменной.

Значение выражения

Значение алгебраического выражения – это число, получаемое в результате выполнения всех арифметических действий, которые указаны в этом выражении. Но, чтобы его получить, буквы необходимо заменить числами. Поэтому в примерах всегда указывают, какое число соответствует букве. Рассмотрим, как найти значение выражения 8а – 14 * (5 – а), если а = 3.

Подставим вместо буквы а число 3. Получаем следующую запись: 8 * 3 – 14 * (5 – 3).

Как и в числовых выражениях, решение алгебраического выражения проводится по правилам выполнения арифметических действий. Решим все по порядку.

5 – 3 = 2.
8 * 3 = 24.
14 * 2 = 28.
24 – 28 = – 4.

Таким образом, значение выражения 8а – 14 * (5 – а) при а = 3 равно -4.

Значение переменной называют допустимым, если при нем выражение имеет смысл, то есть возможно найти его решение.

Пример допустимой переменной для выражения 5 : (2а) – это число 1. Подставив его в выражение, получаем 5 : (2 * 1) = 2,5. Недопустимая переменная для данного выражения – это 0. Если подставить ноль в выражение, получаем 5 : (2 * 0), то есть 5 : 0. На ноль делить нельзя, значит, выражение не имеет смысла.

Тождественные выражения

Если два выражения при любых значениях, входящих в их состав переменных оказываются равны, их называют тождественными.
Пример тождественных выражений:
4 (а + с) и 4а + 4с.
Какие бы значения ни принимали буквы а и с, выражения всегда окажутся равны. Любое выражение можно заменить другим, тождественным ему. Этот процесс называют тождественным преобразованием.

Пример тождественного преобразования.
4 * (5а + 14с) – данное выражение можно заменить тождественным, применив математический закон умножения. Чтобы умножить число на сумму двух чисел, нужно это число умножить на каждое слагаемое и сложить полученные результаты.

4 * 5а = 20а.
4 * 14с = 64с.
20а + 64с.

Таким образом, выражению 4 * (5а + 14с) является тождественным 20а + 64с.

Число, стоящее в алгебраическом выражении перед буквенной переменной, называется коэффициентом. Коэффициент и переменная – это множители.

Решение задач

Алгебраические выражения используют для решения задач и уравнений.
Рассмотрим задачу. Петя придумал число. Для того, чтобы его отгадал одноклассник Саша, Петя сказал ему: сначала я прибавил к числу 7, затем вычел из него 5 и умножил на 2. В результате я получил число 28. Какое число я задумал?

Для решения задачи нужно загаданное число обозначить буквой а, а затем произвести все указанные действия с ним.

а + 7.
(а + 7) – 5.
((а + 7) – 5) * 2 = 28.

Теперь решим полученное уравнение.

Петя задумал число 12.

Что мы узнали?

Алгебраическое выражение – запись, составленная из букв, чисел и знаков арифметических действий. Каждое выражение имеет значение, которое находят путем выполнения всех арифметических действий в выражении. Буква в алгебраическом выражении называется переменной, а число перед ней – коэффициентом. Алгебраические выражения используют для решения задач.

6.4.1. Алгебраическое выражение

I. Выражения, в которых наряду с буквами могут быть использованы числа, знаки арифметических действий и скобки, называются алгебраическими выражениями.

Примеры алгебраических выражений:

2m -n; 3·(2a + b); 0,24x; 0,3a -b · (4a + 2b); a 2 – 2ab;

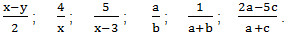
Так как букву в алгебраическом выражении можно заменить какими то различными числами, то букву называют переменной, а само алгебраическое выражение — выражением с переменной.

II. Если в алгебраическом выражении буквы (переменные) заменить их значениями и выполнить указанные действия, то полученное в результате число называется значением алгебраического выражения.

Примеры. Найти значение выражения:

1) a + 2b -c при a = -2; b = 10; c = -3,5.

2) |x| + |y| -|z| при x = -8; y = -5; z = 6.

1) a + 2b -c при a = -2; b = 10; c = -3,5. Вместо переменных подставим их значения. Получим:

— 2+ 2 · 10- (-3,5) = -2 + 20 +3,5 = 18 + 3,5 = 21,5.

2) |x| + |y| -|z| при x = -8; y = -5; z = 6. Подставляем указанные значения. Помним, что модуль отрицательного числа равен противоположному ему числу, а модуль положительного числа равен самому этому числу. Получаем:

|-8| + |-5| -|6| = 8 + 5 -6 = 7.

III. Значения буквы (переменной), при которых алгебраическое выражение имеет смысл, называют допустимыми значениями буквы (переменной).

Примеры. При каких значениях переменной выражение не имеет смысла?

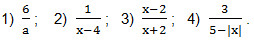
Решение. Мы знаем, что на нуль делить нельзя, поэтому, каждое из данных выражений не будет иметь смысла при том значении буквы (переменной), которая обращает знаменатель дроби в нуль!

В примере 1) это значение а = 0. Действительно, если вместо а подставить 0, то нужно будет число 6 делить на 0, а этого делать нельзя. Ответ: выражение 1) не имеет смысла при а = 0.

В примере 2) знаменатель х — 4 = 0 при х = 4, следовательно, это значение х = 4 и нельзя брать. Ответ: выражение 2) не имеет смысла при х = 4.

В примере 3) знаменатель х + 2 = 0 при х = -2. Ответ: выражение 3) не имеет смысла при х = -2.

В примере 4) знаменатель 5 -|x| = 0 при |x| = 5. А так как |5| = 5 и |-5| = 5, то нельзя брать х = 5 и х = -5. Ответ: выражение 4) не имеет смысла при х = -5 и при х = 5.
IV. Два выражения называются тождественно равными, если при любых допустимых значениях переменных соответственные значения этих выражений равны.

Пример: 5 (a – b) и 5a – 5b тожественно равны, так как равенство 5 (a – b) = 5a – 5b будет верным при любых значениях a и b. Равенство 5 (a – b) = 5a – 5b есть тождество.

Тождество – это равенство, справедливое при всех допустимых значениях входящих в него переменных. Примерами уже известных вам тождеств являются, например, свойства сложения и умножения, распределительное свойство.

Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием или просто преобразованием выражения. Тождественные преобразования выражений с переменными выполняются на основе свойств действий над числами.

a) преобразуйте выражение в тождественно равное, используя распределительное свойство умножения:

1) 10·(1,2х + 2,3у); 2) 1,5·(a -2b + 4c); 3) a·(6m -2n + k).

Решение. Вспомним распределительное свойство (закон) умножения:

(a+b)·c=a·c+b·c (распределительный закон умножения относительно сложения: чтобы сумму двух чисел умножить на третье число, можно каждое слагаемое умножить на это число и полученные результаты сложить).
(а-b)·c=a·с-b·c (распределительный закон умножения относительно вычитания: чтобы разность двух чисел умножить на третье число, можно умножить на это число уменьшаемое и вычитаемое отдельно и из первого результата вычесть второй).

1) 10·(1,2х + 2,3у) = 10 · 1,2х + 10 · 2,3у = 12х + 23у.

2) 1,5·(a -2b + 4c) = 1,5а -3b + 6c.

3) a·(6m -2n + k) = 6am -2an +ak.

б) преобразуйте выражение в тождественно равное, используя переместительное и сочетательное свойства (законы) сложения:

4) х + 4,5 +2х + 6,5; 5) (3а + 2,1) + 7,8; 6) 5,4с -3 -2,5 -2,3с.

Решение. Применим законы (свойства) сложения:

a+b=b+a (переместительный: от перестановки слагаемых сумма не меняется).
(a+b)+c=a+(b+c) (сочетательный: чтобы к сумме двух слагаемых прибавить третье число, можно к первому числу прибавить сумму второго и третьего).

4) х + 4,5 +2х + 6,5 = (х + 2х) + (4,5 + 6,5) = 3х + 11.

5) (3а + 2,1) + 7,8 = 3а + (2,1 + 7,8) = 3а + 9,9.

6) 6) 5,4с -3 -2,5 -2,3с = (5,4с -2,3с) + (-3 -2,5) = 3,1с -5,5.

в) преобразуйте выражение в тождественно равное, используя переместительное и сочетательное свойства (законы) умножения:

7) 4 · х · (-2,5); -3,5 · 2у · (-1); 9) 3а · (-3) · 2с.

Решение. Применим законы (свойства) умножения:

a·b=b·a (переместительный: от перестановки множителей произведение не меняется).
(a·b)·c=a·(b·c) (сочетательный: чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего).

7) 4 · х · (-2,5) = -4 · 2,5 · х = -10х.

8 ) -3,5 · 2у · (-1) = 7у.

9) 3а · (-3) · 2с = -18ас.

Если алгебраическое выражение дано в виде сократимой дроби, то пользуясь правилом сокращения дроби его можно упростить, т.е. заменить тождественно равным ему более простым выражением.

Примеры. Упростите, используя сокращение дробей.

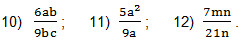
Решение. Сократить дробь — это значит разделить ее числитель и знаменатель на одно и то же число (выражение), отличное от нуля. Дробь 10) сократим на 3b; дробь 11) сократим на а и дробь 12) сократим на 7n. Получаем:

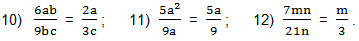
Алгебраические выражения применяют для составления формул.

Формула – это алгебраическое выражение, записанное в виде равенства и выражающее зависимость между двумя или несколькими переменными. Пример: известная вам формула пути s=v·t (s — пройденный путь, v — скорость, t — время). Вспомните, какие еще формулы вы знаете.

Понятие и виды алгебраических выражений

п.1. Математические символы и выражения

В математическом языке мы используем особенные «слова», которые называются математическими выражениями, при этом «буквами» нам служат математические символы.

Список математических символов постоянно пополняется. Ведь при написании своей работы каждый вправе изобрести собственный иероглиф-символ, объяснить его смысл с помощью определения и предложить правила применения. Если символ окажется удачным и востребованным, то со временем он появится в других работах и начнёт самостоятельный путь по миру.

Допустим, по правилам, мы строим математические выражения, которые состоят из различных чисел (образованных цифрами, дробной чертой и десятичной запятой), знаков арифметических операций, возведения в рациональную степень, корней и скобок:

Например: $(1+5^2):3frac 14 , frac <4+3,5> <(12-6^3)+5>, frac 12 – frac 13 cdot (-sqrt 9) $

Такие выражения называют числовыми термами .

Например: $(1+5^2):3frac 14 gt 7, frac <4+3,5> <(12-6^3)+5>lt 0, frac 12 – frac 13 cdot (-sqrt 9) = 1frac 12$

Такие выражения называют числовыми формулами .

Формула по сравнению с термом приобретает дополнительный смысл: она может быть «истинной» или «ложной». Три представленные выше формулы истинные. А вот 2+2=5 – ложная числовая формула.

п.2. Определение и понятие переменной

На практике при проведении расчётов очень часто возникают повторяющиеся ситуации, когда меняется только одна величина, а другие остаются постоянными. Например, нам нужно рассчитать площадь плит разной длины 7, 10 и 15 м, но одной и той же ширины 4 м. Тогда $S_1 = 4 cdot 7 = 28 м^2, S_2 = 4 cdot 10=40 м^2, S_3 = 4 cdot 15=60 м^2 $. Эти расчёты можно обобщить, если записать S=4a, где первый множитель – постоянная ширина 4 м, а второй – переменная длина a м. Такое обобщение называется «введением переменной»; оно удобно тем, что даёт универсальный рецепт для расчётов.

Математические выражения с переменными также могут быть термами или формулами.

Термы с переменными: $(1+a^2):3 frac 14 – b, frac <4+mn><(12-k^3)+5>, frac 12 – frac <1> cdot (-sqrt 9) $

Формулы с переменными: $(1+a^2):3 frac 14 – b > b, frac <4+mn> <(12-k^3)+5>Алгебраические выражения – это математические выражения, которые состоят из различных чисел и переменных, знаков арифметических операций, возведения в рациональную степень, корней, скобок и знаков отношений.

Если алгебраическое выражение не содержит деления на переменные и извлечения корня из переменных (или возведения переменных в степень с дробным показателем), то его называют целым выражением.

Примеры целых выражений:

$7, frac <3a^2><5>+48, (sqrt 7b-4c^3)^5$ – термы $b-frac 32 = 8,28c^2 > sqrt 2$ – формулы

Если алгебраическое выражение, кроме признаков целого выражения, содержит также деление на переменные, то его называют дробным выражением.

Примеры дробных выражений:

$frac 7m, 3a^2 + frac <48>, (sqrt 7b-frac <4>)^5$ – термы $b-frac <2> <2+a>= 8,28c^2 > frac <5k>$ – формулы

Целые и дробные выражения объединяют в класс рациональных выражений.

Если алгебраическое выражение содержит извлечение корня из переменных (или возведение переменных в степень с дробным показателем), то его называют иррациональным выражением.

Примеры иррациональных выражений:

п.4. Примеры

Пример 1. Запишите числовую формулу и проверьте, истинна ли она: удвоенное произведение чисел 75 и $3 frac 13$ равно полу разности чисел 1440 и 480.

Числовая формула по условию: $2 cdot 72 cdot 3 frac 13 = frac<1440-480><2>$

Значение выражения слева $2cdot72cdot3 frac 13 = 2cdot24cdot3cdot frac<10><3>=480$

Значение выражения справа $frac <1440-480> <2>= frac <960> <2>= 480$

Значения выражений слева и справа действительно равны, формула истинна.

Ответ: формула истинна

Пример 2. Найдите значение алгебраического выражения 2a – 5b + 11, если $a = 3frac 14$ и b=3,5

Подставляем значения переменных:

$2cdot3frac 14 – 5 cdot 3,5 + 11 = frac<13> <2>-17,5 + 11 = 0$

Пример 3. Известно, что x – y = 21. Найдите значение выражения $frac<3(x+y)-6y><7>$

При x-y=21 получаем: $frac <3(x-y)> <7>= frac <3cdot21> <7>= 3 cdot 3 = 9 $

Пример 4. Для проведения экзамена закупили k пачек бумаги по p рублей и m картриджей для принтера по q рублей. Напишите формулу, по которой можно найти общую сумму расходов S.

Сумма, потраченная на бумагу $s_1 = kp$

Сумма, потраченная на картриджи $s_2 = mq$

Общая сумма расходов $S = s_1 + s_2$. Получаем: $S = kp + mq$

Значения выражений слева и справа действительно равны, формула истинна.

Основные виды выражений в алгебре

Уроки алгебры знакомят нас с различными видами выражений. По мере поступления нового материала выражения усложняются. При знакомстве со степенями они постепенно добавляются в выражение, усложняя его. Также происходит с дробями и другими выражениями.

Чтобы изучение материала было максимально удобным, это производится по определенным названиям для того, чтобы можно было их выделить. Данная статья даст полный обзор всех основных школьных алгебраических выражений.

Одночлены и многочлены

Выражения одночлены и многочлены изучаются в школьной программе, начиная с 7 класса. В учебники были даны определения такого вида.

Одночлены – это числа, переменные, их степени с натуральным показателем, любые произведения, сделанные с их помощью.

Многочленами называют сумму одночленов.

Если взять, к примеру число 5 , переменную x , степень z 7 ,тогда произведения вида 5 · x и 7 · x · 2 · 7 · z 7 считаются одночленами. Когда берется сумма одночленов вида 5 + x или z 7 + 7 + 7 · x · 2 · 7 · z 7 , тогда получаем многочлен.

Чтобы отличать одночлен от многочлена, обращают внимание на степени и их определения. Немаловажно понятие коэффициента. При приведении подобных слагаемых их разделяют на свободный член многочлена или старший коэффициент.

Над одночленами и многочленами чаще всего выполняются какие-то действия, после которых выражение приводится к вижу одночлена. Выполняется сложение, вычитание, умножение и деление, опираясь на алгоритм для выполнения действий с многочленами.

Когда имеется одна переменная, не исключено деление многочлена на многочлен, которые представляются в виде произведения. Такое действие получило название разложение многочлена на множители.

Рациональные (алгебраические) дроби

Понятие рациональные дроби изучаются в 8 классе средней школы. Некоторые авторы называют их алгебраическими дробями.

Рациональной алгебраической дробью называют дробь, в которой на месте числителя и знаменателя выступают многочлены или одночлены, числа.

Рассмотрим на примере записи рациональных дробей типа 3 x + 2 , 2 · a + 3 · b 4 , x 2 + 1 x 2 – 2 и 2 2 · x + – 5 1 5 · y 3 · x x 2 + 4 . Опираясь на определение, можно сказать, что каждая дробь считается рациональной дробью.

Алгебраические дроби можно складывать, вычитать, умножать, делить, возводить в степень. Подробнее это рассматривается в разделе действий с алгебраическими дробями. Если необходимо преобразовать дробь, нередко пользуются свойством сокращения и приведения к общему знаменателю.

Рациональные выражения

В школьном курсе изучается понятие иррациональных дробей, так как необходима работа с рациональными выражениями.

Рациональные выражения считаются числовыми и буквенными выражениями, где используются рациональные числа и буквы со сложением, вычитанием, умножением, делением, возведением в целую степень.

Рациональные выражения могут не иметь знаков, принадлежащих функции, которые приводят к иррациональности. Рациональные выражения не содержат корней, степеней с дробными иррациональными показателями, степеней с переменными в показателе, логарифмических выражений, тригонометрических функций и так далее.

Основываясь на правиле, приведенном выше, приведем примеры рациональных выражений. Из выше сказанного определения имеем, что как числовое выражение вида 1 2 + 3 4 , так и 5 , 2 + ( – 0 , 1 ) 2 · 2 – 3 5 – 4 3 4 + 2 : 12 · 7 – 1 + 7 – 2 2 3 3 – 2 1 + 0 , 3 считаются рациональными. Выражения, содержащие буквенные обозначения, также относят к рациональным a 2 + b 2 3 · a – 0 , 5 · b , с переменными вида a · x 2 + b · x + c и x 2 + x y – y 2 1 2 x – 1 .

Все рациональные выражения подразделяют на целые и дробные.

Целые рациональные выражения

Целые рациональные выражения – это такие выражения, не содержащие деления на выражения с переменными отрицательной степени.

Из определения имеем, что целое рациональное выражение – это и выражение, содержащее буквы, например, а + 1 , выражение, содержащее несколько переменных, например, x 2 · y 3 − z + 3 2 и a + b 3 .

Выражения вида x : ( y − 1 ) и 2 x + 1 x 2 – 2 x + 7 – 4 не могут быть целыми рациональными, так как имеют деление на выражение с переменными.

Дробные рациональные выражения

Дробное рациональное выражение – это выражение, которое содержит деление на выражение с переменными отрицательной степени.

Из определения следует, что дробные рациональные выражения могу быть 1 : x , 5 x 3 – y 3 + x + x 2 и 3 5 7 – a – 1 + a 2 – ( a + 1 ) ( a – 2 ) 2 .

Если рассматривать выражения такого типа ( 2 · x − x 2 ) : 4 и a 2 2 – b 3 3 + c 4 + 1 4 , 2 , то дробными рациональными они не считаются, так как не имеют в знаменателе выражений с переменными.

Выражения со степенями

Выражения, которые содержат степени в любой части записи, называют выражениями со степенями или степенными выражениями.

Для понятия приведем пример такого выражения. В них могут отсутствовать переменные, например, 2 3 , 32 – 1 5 + 1 , 5 3 , 5 · 5 – 2 5 – 1 , 5 . Также характерны степенные выражения вида 3 · x 3 · x – 1 + 3 x , x · y 2 1 3 . Для того, чтобы решить их, необходимо выполнять некоторые преобразования.

Иррациональные выражения, выражения с корнями

Корень, имеющий место быть в выражении, дает ему иное название. Их называют иррациональными.

Иррациональными выражениями называют выражения, которые имеют в записи знаки корней.

Из определения видно, что это выражения вида 64 , x – 1 4 3 + 3 3 , 2 + 1 2 – 1 – 2 + 3 2 , a + 1 a 1 2 + 2 , x · y , 3 x + 1 + 6 x 2 + 5 x и x + 6 + x – 2 3 + 1 4 x 2 3 + 3 – 1 1 3 . В каждом из них имеется хотя бы один значок корня. Корни и степени связаны, поэтому можно видеть такие записи выражений, как x 7 3 – 2 5 , n 4 8 · m 3 5 : 4 · m 2 n + 3 .

Тригонометрические выражения

Тригонометрическое выражение – это выражения с содержанием sin , cos , tg и ctg и их обратные – arcsin , arccos , arctg и arcctg .

Примеры тригонометрических функций очевидны: sin π 4 · cos π 6 cos 6 x – 1 и 2 sin x · t g 2 x + 3 , 4 3 · t g π – arcsin – 3 5 .

Для работы с такими функциями необходимо пользоваться свойствами, основными формулами прямых и обратных функций. Статья преобразование тригонометрических функций раскроет этот вопрос подробней.

Логарифмические выражения

После знакомства с логарифмами можно говорить о сложных логарифмических выражениях.

Выражения, которые имеют логарифмы, называют логарифмическими.

Примером таких функций могут быть log 3 9 + ln e , log 2 ( 4 · a · b ) , log 7 2 ( x · 7 3 ) log 3 2 x – 3 5 + log x 2 + 1 ( x 4 + 2 ) .

Можно встретить такие выражения, где есть степени и логарифмы. Это итак понятно, так как из определения логарифма следует, что это является показателем степени. Тогда получаем выражения вида x l g x – 10 , log 3 3 x 2 + 2 x – 3 , log x + 1 ( x 2 + 2 x + 1 ) 5 x – 2 .

Для углубления изучения материала, следует обратиться к материалу о преобразовании логарифмических выражений.

Дроби

Существуют выражения особого вида, которые получили название дроби. Так как они имеют числитель и знаменатель, то они могут содержать не просто числовые значения, а также выражения любого типа. Рассмотрим определение дроби.

Дробью называют такое выражение, имеющее числитель и знаменатель, в которых имеются как числовые, так и буквенные обозначения или выражения.

Примеры дробей, которые имеют числа в числителе и знаменателе, выглядят так 1 4 , 2 , 2 – 6 2 7 , π 2 , – e π , ( − 15 ) ( − 2 ) . Числитель и знаменатель может содержать как численные, так и буквенные выражения вида ( a + 1 ) 3 , ( a + b + c ) ( a 2 + b 2 ) , 1 3 + 1 – 1 3 – 1 1 1 + 1 1 + 1 5 , cos 2 α – sin 2 α 1 + 3 t g α , 2 + ln 5 ln x .

Хотя такие выражения, как 2 5 − 3 7 , x x 2 + 1 : 5 не являются дробями, однако, имеют дробь в своей записи.

Выражение общего вида

Старшие классы рассматривают задачи повышенной трудности, где собраны все комбинированные задания группы С по ЕГЭ. Эти выражения отличаются особой сложностью и различными комбинациями корней, логарифмов, степеней, тригонометрических функций. Это задания типа x 2 – 1 · sin x + π 3 или sin a r c t g x – a · x 1 + x 2 .

Их вид говорит о том, что можно отнести к любому из вышеперечисленных видов. Чаще всего их не относят ни к какому, так как они имеют специфичное комбинированное решение. Их рассматривают как выражения общего вида, причем для описания не используются дополнительные уточнения или выражения.

При решении такого алгебраического выражения всегда необходимо обращать внимание на его запись, наличие дроби, степеней или дополнительных выражений. Это нужно для того, чтобы точно определиться со способом его решения. Если нет уверенности в его названии, то рекомендуется называть его выражением общего типа и решать, согласно выше написанному алгоритму.

Числовые и буквенные выражения

О чем эта статья:

Числовые выражения: что это

Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.

Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.

Например:

23 + 5 = 28
5 – 2 = 3
52 * 3 = 156
28 : 7 = 4

Это простые числовые выражения.

Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:

(5 * 3) – (5 * 2) = 5
6 : (7 – 4) = 2
(45 + 45) : 9 = 10
11 * (5 * 5) = 275

Это сложные числовые выражения.

Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».

Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.

Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
– — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.

11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.

При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:

Сначала выполняется действие, записанное в скобках.
Затем выполняется деление/умножение.
В последнюю очередь выполняется сложение/вычитание.

Пример 1. Найдите значение числового выражения: 3 * (2 + – 4

2 + 8 = 10
3 * 10 = 30
30 – 4 = 26

Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)

6 + 7 = 13
13 + 2 = 15
13 * 15 = 195

(6 + 7) * (13 + 2) = 195

Часто бывает нужно сравнить два числовых выражения.

Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.

Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2

6 + 8 = 14

Затем находим значение второго выражения:

2 * 2 = 4

Сравниваем получившиеся результаты:

14 больше 4
14 > 4
6 + 8 > 2 * 2

Пример 2. Сравните следующие числовые выражения:
5 * (12 – 2) – 7 и (115 + 9) – (7 – 3)

12 – 2 = 10
5 * 10 = 50
50 – 7 = 43
5 * (12 – 2) – 7 = 43

Затем находим значение:

115 + 9 = 124
7 – 3 = 4
124 – 4 = 120

Сравниваем полученные результаты:

43 меньше 120
43

Буквенные выражения

Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.

В буквенном выражение есть цифры, знаки арифметических действия и буквы.

Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.

Например:
(5 + a) * 7
7 * (x – 2)
(6 – 2) + (3 + x)

Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.

У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:

Сначала следует прочитать его полностью.
Затем оно записывается.
Третьим шагом идет подстановка значения неизвестного в выражение.
А затем производится вычисление, согласно очередности выполнения арифметических действий.

Пример 1. Найдите значение выражения: 5 + x.

Читаем: найдите сумму числа 5 и x.
Подставляем вместо неизвестного x число 4.
Вычисляем: 5 + 4 = 9.

Пример 2. Найдите значение выражения: (4 + a) * (2 + x).

Читаем: найдите произведение суммы числа 4 и а и суммы числа 2 и x.
Подставляем вместо неизвестного a число 2.
Вычисляем 4 + 2 = 6.
Подставляем вместо неизвестного x число 5.
Вычисляем 2 + 5 = 10.
Находим произведение 6 * 10 = 60.
Записываем результат: (4 + 2) * (2 + 5) = 60.

Выражения с переменными

Переменная — это значение буквы в буквенном выражении.

Например, в выражении x + a – 8
x — переменная
a — переменная

Если вместо переменных подставить числа, то буквенное выражение x + a – 8 станет числовым выражением. Вот так:

подставляем вместо переменной x число 5, а вместо переменной a — число 10, получаем 5 + 10 – 8.

Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.

После подстановки значения переменных находим значение x + a – 8 = 5 + 10 – 8 = 7.

Часто можно встретить буквенные выражения, записанные следующим образом:
5x – 4a

Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.

5x – 4a = 5*x – 4*a

5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a

Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.

Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.

Задание раз.

Сумма 6 и a.
Разность 8 и x.
Сумма x – 2 и 6
Разность 15 и x – y
Сумма 45 + 5 и 12 – 6

6 + a.
8 – x
(x – 2) + 6
15 – (x – y)
(45 + 5) + (12 – 6).

Задание два.

Составьте буквенное выражение:

Сумма разности b и 345 и суммы 180 и x.

Ответ: (b – 345) + (180 + x).

Задание три.
Составьте буквенное выражение:
Разность разности 30 и y и разности a и b.
Ответ: (30 – y) – (a – b).

Задание четыре.
Составьте выражение для решения задачи и найдите его значение.
Ролл «Калифорния» стоит 480 рублей — это на 40 рублей меньше, чем ролл «Филадельфия». Сколько будут стоить оба ролла?
Как решаем:
Калифорния — 480 рублей.
Филадельфия — 480 + 40.
Калифорния + Филадельфия = ?
480 + (480 + 40).
Мы помним, что выполнение арифметических действий в числовом выражении имеет строгую последовательность. Сначала — действие в скобках:
480 + 520 = 1 000.

Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.

Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?

Маша — 150 видео.
Лена — 150 + 13 видео.
Маша + Лена = ? видео.

150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.

Ответ: Маша и Лена посмотрели всего 313 видео.

Задание шесть.
Вычислите:
(500 + 300) : a – 15,
при условии, что a = 10.

Подставляем число 10 (значение переменной) вместо переменной
(500 + 300) : 10 – 15

Затем выполняем сначала арифметическое действие в скобках: 500 + 300 = 800.
Затем выполняем деление 800 : 10 = 80.
Выполняем вычитание 80 – 15 = 65.

Ответ: (500 + 300) : 10 – 15 = 65.

Задание семь.
Вычислите:
(270 – 120) * (x – 10),
при условии, что x = 45.

Как решаем: подставляем число 45 (значение переменной) вместо переменной x
(270 – 120) * (45 – 10).

Затем выполняем сначала арифметическое действие в скобках: 270 – 120 = 150.
Выполняем арифметическое действие во вторых скобках: 45 – 10 = 35.
Затем выполняем умножение 150 * 35 = 5 250

Ответ: (270 – 120) * (45 – 10) = 5 250.

Задание восемь.
Вычислите:
(50 * x) – (3 * y)
при условии, что x = 2; y = 10

Подставляем число 2 вместо переменной x
(50 * 2) – (3 * y).

Подставляем число 10 вместо переменной y
(50 * 2) – (3 * 10).

Затем выполняем сначала арифметическое действие в скобках: 50 * 2 = 100.
Выполняем арифметическое действие во вторых скобках: 3 * 10 = 30.
Затем выполняем вычитание 100 – 30 = 70

Алгебраические выражения и их характеристики
методическая разработка по алгебре на тему

В публикации представлена логика различия алгебраических выражений для учащихся основного общего и среднего (полного) общего образования как переходной этап формирования логики различий математических выражений применяемых в физике и т.д. для формирования в дальнейшем понятий о явлениях, задачах, их классификации и методологии подхода их решения.

Скачать:

Вложение	Размер
algebraicheskie_vyrazheniya_i_ih_harakteristiki.docx	156.8 КБ

Предварительный просмотр:

Алгебраические выражения и их характеристики

Алгебра, как наука, изучает закономерности действий над множествами, обозначенных буквами. К алгебраическим действиям относят сложение, вычитание, умножение, деление, возведение в степень, извлечение корня. В результате данных действий образовались алгебраические выражения. Алгебраическое выражение – выражение, состоящее из чисел и букв, обозначающих множества, с которым осуществляют алгебраические действия. Данные действия перешли в алгебру из арифметики. В алгебре рассматривают и приравнивание одного алгебраического выражения другому, что является их тождественным равенством. Примеры алгебраических выражений приведены в §1. Методы преобразований и взаимосвязи выражений были тоже позаимствованы у арифметики . Знания арифметических закономерностей действий над арифметическими выражениями позволяют проводить преобразования над похожими алгебраическими выражениями, преобразовывать их, упрощать, сравнивать, анализировать. Алгебра – наука закономерностей преобразований выражений, состоящих из множеств, представленных в виде буквенных обозначений, связанных между собой знаками различных действий. Существуют и более сложные алгебраические выражения, изучаемые в высших учебных заведениях. Пока их можно разделить на виды, наиболее часто применяемые в школьном курсе.

1 Виды алгебраических выражений

п.1 Простые выражения: 4a; (a + b); (a + b)3с; ; .

п.2 Тождественные равенства: (a + b)с = aс + bс; ;

п.3 Неравенства: aс ; a + с .

п.4 Формулы: х=2а+5; у=3b; у=0,5d 2 +2;

– первого уровня сложности

– второго уровня сложности

– третьего уровня сложности сточки зрения поиска значений для множеств

– четвертого уровня сложности сточки зрения поиска значений для множеств а, у:

ах+с = -5bх; 4х 2 +2х= 42;

п.7 Функциональные зависимости: у=3х; у=ах 2 +4b; у=0,5х 2 +2;

2 Рассмотрим алгебраические выражения

2.1 В п.1 представлены простые алгебраические выражения. Бывает вид и

сложнее, к примеру:

Как правило, такие выражения не имеют знака «=». Задачей при рассмотрении таких выражений является их преобразование и получение в упрощенном виде. При преобразовании алгебраического выражения, относящегося к п.1, получают новое алгебраическое выражение, которое по своему значению равнозначно предыдущему. Такие выражения, говорят, тождественно равнозначны. Т.е. алгебраическое выражение слева от знака равно, равнозначно по своему значению алгебраическому выражению справа. В таком случае получают алгебраическое выражение нового вида, называемое тождественным равенством (см. п. 2).

2.2 В п.2 представлены алгебраические тождественные равенства , которые образуются при алгебраических методах преобразования, рассматриваются алгебраические выражения, наиболее часто применяемые как методы при решении задач по физике. Примеры тождественных равенств алгебраических преобразований, применяемых часто в математике и физике:

Переместительный закон сложения: a + b = b + a.

Сочетательный закон сложения: (a + b) + с = a + (b + c).

Переместительный закон умножения: ab = ba.

Сочетательный закон умножения: (ab)с = a(bc).

Распределительный закон умножения относительно сложения:

Распределительный закон умножения относительно вычитания:

Тождественные равенства дробных алгебраических выражений (предполагается, что знаменатели дробей отличны от нуля):

Тождественные равенства алгебраических выражений со степенями:

где ( n раз, ) – степень с целым показателем

б) (a + b) 2 =а 2 +2ab+b 2 .

Тождественные равенства алгебраических выражений с корнями n- й степени:

Выражение – арифметический корень n -й степени из числа В частности, – арифметический квадратный.

Степень с дробным (рациональным) показателем корень:

Тождественные выше приведенные равнозначные выражения применяют для преобразований более сложных алгебраических выражений, не содержащих знака «=».

Рассмотрим пример, в котором для преобразований более сложного алгебраического выражения используют знания, приобретенные при преобразованиях более простых алгебраических выражений в виде тождественных равенств.

2.3 В п.3 представлены алгебраические н еравенства, у которых алгебраическое выражение левой части не равно правой, т.е. не являются тождественными. В таком случае они и являются неравенствами. Как правило, при решении некоторых задач по физике важны свойства неравенств:

1) Если a , то при любом c : a + с .

2) Если a и c > 0 , то aс .

3) Если a и c , то aс > bс .

4) Если a , a и b одного знака, то 1/a > 1/b .

5) Если a и c , то a + с , a – d .

6) Если a , c , a > 0 , b > 0 , c > 0 , d > 0 , то ac .

7) Если a , a > 0 , b > 0 , то

Если , то

2.4 В п.4 представлены алгебраические формулы т.е. алгебраические выражения, у которых с левой части от знака равенства стоит буква, обозначающая множество, значение которого неизвестно и его следует определить. А с правой части от знака равно стоят множества, значения которых известны. В данном случае это алгебраическое выражение называют алгебраической формулой.

Алгебраическая формула – это алгебраическое выражение, содержащее знак равенства, с левой стороны от которого находится множество, значение которого неизвестно, а справа – множества с известными значениями, исходя из условия задачи. Для определения неизвестного значения множества, стоящего слева от знака «равно», производят подстановку известных значений величин в правой части от знака «равно» и осуществляют арифметические вычислительные действия, обозначенные в алгебраическом выражении в этой части.

Дано: Решение:

а=25 Пусть дано алгебраическое выражение:

х=? х=2а+5.

Данное алгебраическое выражение является алгебраической формулой т.к. слева от знака «равно» стоит множество, значение которого следует найти, а справа – множества с известными значениями.

Следовательно, можно осуществлять подстановку известного значения для множества «а», для определения неизвестного значения множества «х»:

х=2·25+5=55. Ответ: х=55.

Дано: Решение:

а=25 Алгебраическое выражение является формулой.

b=4 Поэтому можно осуществлять подстановку известных

c=8 значений для множеств, находящихся справа от знака «равно»,

d=3 для определения неизвестного значения множества «k»,

m=20 стоящего слева:

k=?

1 Что собой представляет алгебраическое выражение?

2 Какие виды алгебраических выражений вы знаете?

3 Какое алгебраическое выражение называют тождественным равенством?

4 Для чего необходимо знать шаблоны тождественных равенств?

5 Какое алгебраическое выражение называют формулой?

6 Какое алгебраическое выражение называют уравнением?

7 Какое алгебраическое выражение называют функциональной зависимостью?

По теме: методические разработки, презентации и конспекты

Урок 7 класса, тема «Числовые и алгебраические выражения», учебник под редакцией А.Г.Мордковича. На тему отводится 4 часа, данный урок последний. Эпиграф урока: «Скажи мне – и я забуд.

Вашему вниманию предлагается 1 урок, разработанный по учебнику под редакцией А. Г. Мордковича « Алгебра. 7 класс» Объяснение нового материала идет в ходе диалога «учитель-ученик». Это особе.

Тест на 4 варианта.

Данный материал представлен технологической картой урока и ЦОР.

Конспект урока алгебры “Повторение: алгебраические выражения” 9 класс.

материалдля подготовки к ЕГЭ.