Признаки параллелограмма
| 1 0 . Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм. |
Доказательство:
Дано: АВСD – четырехугольник, АD = ВС, АD ВС.
ВС.
Доказать: АВСD – параллелограмм.
Доказательство:
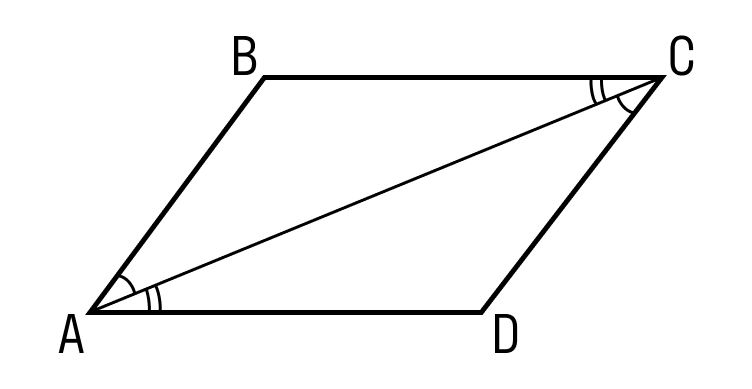
1. Проведем диагональ АС четырехугольника АВСD.
2. Рассмотрим  АВС и
АВС и  АDС: АС – общая,
АDС: АС – общая,  1 =
1 = 3 (т.к. по условию АD
3 (т.к. по условию АD ВС,
ВС, 
 1 и
1 и  3 накрест лежащие углы при пересечении параллельных прямых АD и BC секущей АС),
3 накрест лежащие углы при пересечении параллельных прямых АD и BC секущей АС), 
 АВС =
АВС = АDС (по 1 признаку равенства треугольников),
АDС (по 1 признаку равенства треугольников),  АВ = DC и
АВ = DC и  2 =
2 =  4. Но
4. Но  2 и
2 и  4 накрест лежащие углы при пересечении прямых АВ и DС секущей АС,
4 накрест лежащие углы при пересечении прямых АВ и DС секущей АС,  АВ
АВ DС.
DС.
3. Итак, АD ВС и АВ
ВС и АВ DС, т.е. в четырехугольнике АВСD противоположные стороны попарно параллельны,
DС, т.е. в четырехугольнике АВСD противоположные стороны попарно параллельны,  четырехугольник АВСD – параллелограмм. Что и требовалось доказать.
четырехугольник АВСD – параллелограмм. Что и требовалось доказать.
| 2 0 . Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм. |
Доказательство:
Дано: АВСD – четырехугольник, АВ = DС, АD = ВC.
Доказать: АВСD – параллелограмм.
Доказательство:
1. Проведем диагональ АС четырехугольника АВСD.
2. Рассмотрим  АВС и
АВС и  АDС: АС – общая, по условию АВ = DС, АD = ВC,
АDС: АС – общая, по условию АВ = DС, АD = ВC, 
 АВС =
АВС = АDС (по 3 признаку равенства треугольников),
АDС (по 3 признаку равенства треугольников), 
 1 =
1 =  2, при этом
2, при этом  1 и
1 и  2 накрест лежащие при пересечении прямых АD и ВC секущей АС,
2 накрест лежащие при пересечении прямых АD и ВC секущей АС,  по признаку параллельности двух прямых АD
по признаку параллельности двух прямых АD ВС.
ВС.
3. Итак, АD = ВC, АD ВС,
ВС,  по 1 0 признаку параллелограмма, четырехугольник АВСD – параллелограмм. Что и требовалось доказать.
по 1 0 признаку параллелограмма, четырехугольник АВСD – параллелограмм. Что и требовалось доказать.
| 3 0 . Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник параллелограмм. |
Доказательство:
Дано: АВСD – четырехугольник, АС и DВ диагонали, АС ∩ DВ = О, АО = ОС, DО = ОВ.
Доказать: АВСD – параллелограмм.
Доказательство:
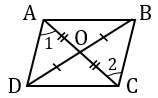
1. Рассмотрим  АОD и
АОD и  ВОС: по условию АО = ОС, DО = ОВ,
ВОС: по условию АО = ОС, DО = ОВ,  АОD и
АОD и  ВОС (как вертикальные углы),
ВОС (как вертикальные углы), 
 АОD =
АОD = ВОС (по 1 признаку равенства треугольников),
ВОС (по 1 признаку равенства треугольников),  АD = ВC и
АD = ВC и  1 =
1 =  2.
2.
2.  1 и
1 и  2 накрест лежащие при пересечении прямых АD и ВC секущей АС, при этом
2 накрест лежащие при пересечении прямых АD и ВC секущей АС, при этом  1 =
1 =  2,
2,  по признаку параллельности двух прямых АD
по признаку параллельности двух прямых АD ВС.
ВС.
3. Итак, АD = ВC, АD ВС,
ВС,  по 1 0 признаку параллелограмма, четырехугольник АВСD – параллелограмм. Что и требовалось доказать.
по 1 0 признаку параллелограмма, четырехугольник АВСD – параллелограмм. Что и требовалось доказать.
Поделись с друзьями в социальных сетях:
Параллелограмм: свойства и признаки

О чем эта статья:
Определение параллелограмма
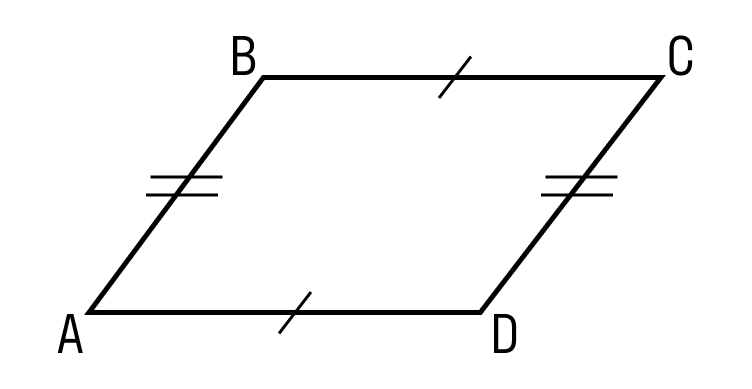
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
- В параллелограмме точка пересечения диагоналей делит их пополам.
- Любая диагональ параллелограмма делит его на два равных треугольника.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
Биссектриса параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
- Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
- Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
- Отрезки биссектрис противоположных углов равны и параллельны.
Как найти площадь параллелограмма:
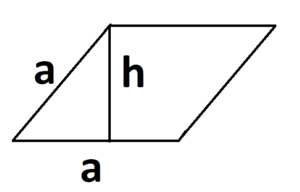
- S = a * h, где a — сторона, h — высота.

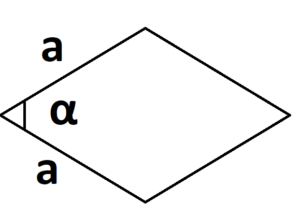
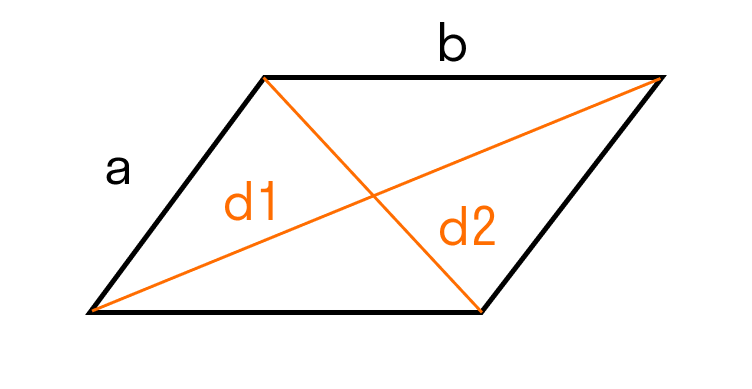
- S = a * b * sinα, где a и b — две стороны, sinα — синус угла между ними.

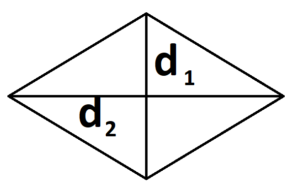
- S = 0,5 * (d1 * d2), где d1,d2 — две диагонали.

Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 * (a + b), где a — ширина, b — высота.

У нас есть отличные дополнительные занятия по математике! Для учеников с 1 по 11 классы!
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
- Противоположные стороны параллелограмма ABCD равны: AB = DC, BC = AD.

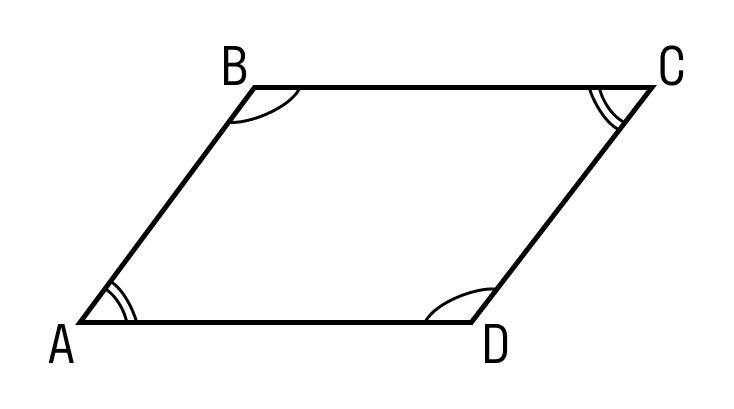
- Противоположные углы параллелограмма ABCD равны:∠A = ∠C, ∠B = ∠D.

- Диагонали параллелограмма ABCD равны и точкой пересечения делятся пополам: BO = OD, AO = OC.

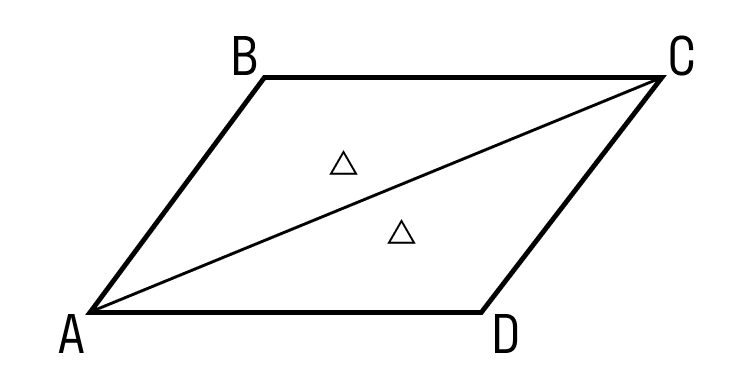
- Диагональ делит параллелограмм ABCD на два равных треугольника: △ABC = △CDA.

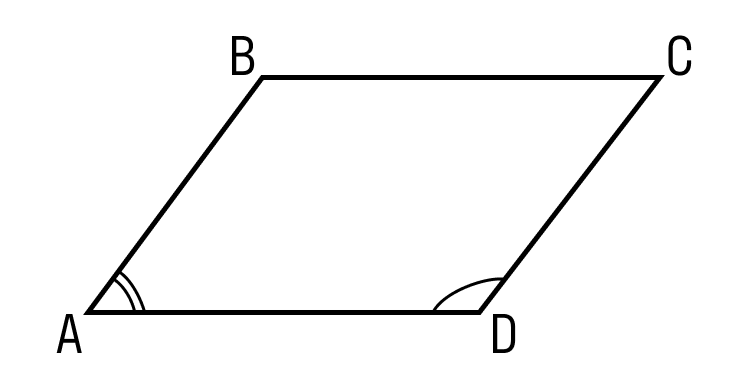
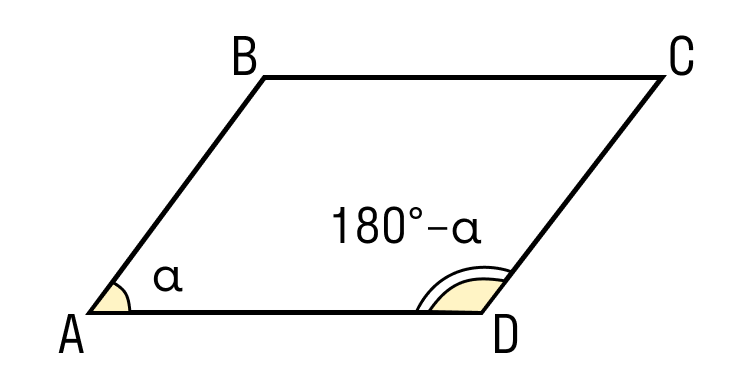
- Сумма углов в параллелограмме ABCD, прилежащих к одной стороне, равна 180 градусам: ∠A + ∠D = 180°.

- В параллелограмме ABCD накрест лежащие углы при диагонали равны: ∠BAC = ∠ACD, ∠BCA = ∠CAD.

- В параллелограмме ABCD сумма всех углов равна 360° градусам.

- Точка пересечения диагоналей является центром симметрии параллелограмма ABCD.

- В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d12 + d22 = 2 * (a2 + b2 ).

- Биссектриса отсекает от параллелограмма ABCD равнобедренный треугольник.

А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.

В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
- Как противоположные стороны параллелограмма: AB = CD
- Как внутренние накрест лежащие равны пары углов: ∠1 = ∠2, ∠3 = ∠4.
- Следовательно, треугольник AOB равен треугольнику COD, из чего следует:
- CO = OA
- BO = DO

Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
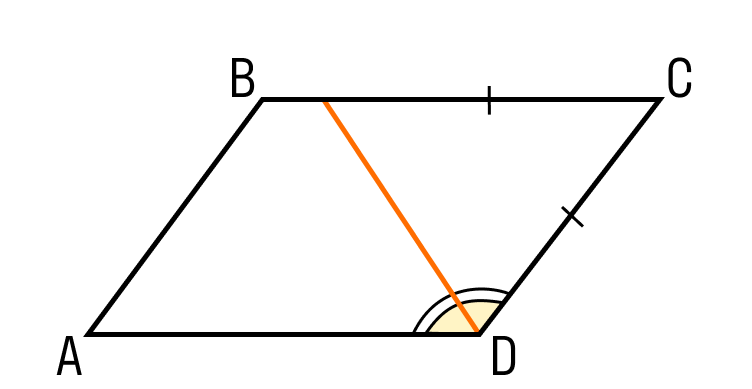
Первый признак параллелограмма. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB || CD
- AB = CD
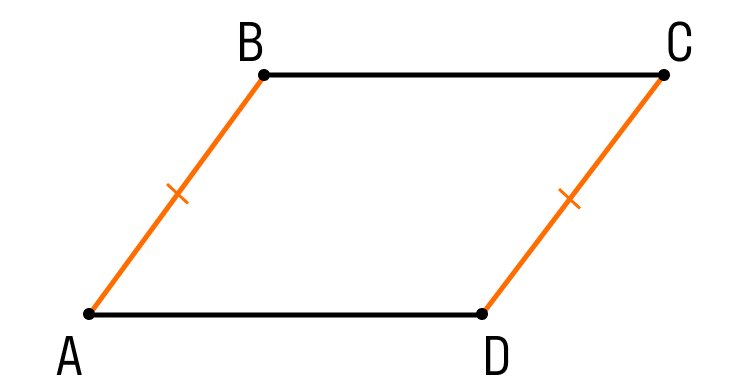
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
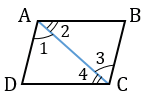
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
- AC — общая сторона;
- По условию AB = CD;
- ∠1 = ∠2, как внутренние накрест лежащие углы для параллельных прямых.
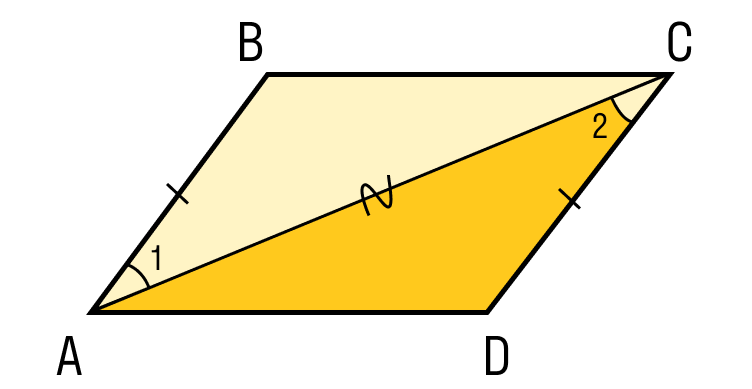
Шаг 3. Из равенства треугольников также следует:
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB = CD
- BC = AD
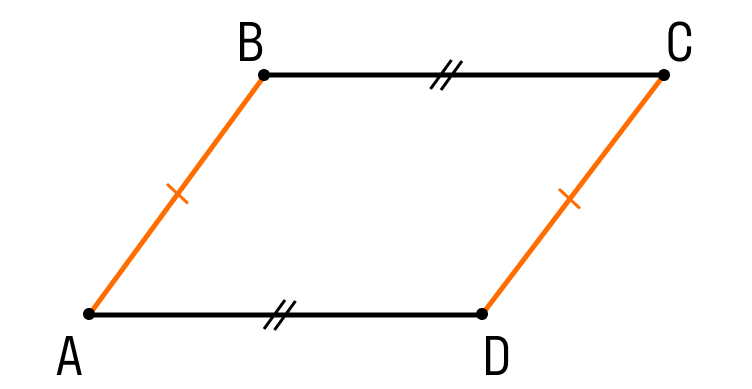
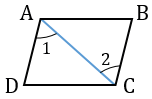
Шаг 2. Рассмотрим треугольники ABC и ADC:
- AC — общая сторона;
- B = CD по условию;
- BC = AD по условию.
Из этого следует, что треугольники ABC и ADC равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
А так как эти углы накрест лежащие при верхней и нижней сторонах и секущей диагонали, значит верхняя и нижняя стороны параллельны.
Эти углы накрест лежащие при боковых сторонах и секущей диагонали. Поэтому боковые стороны четырёхугольника тоже параллельны. Значит четырёхугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
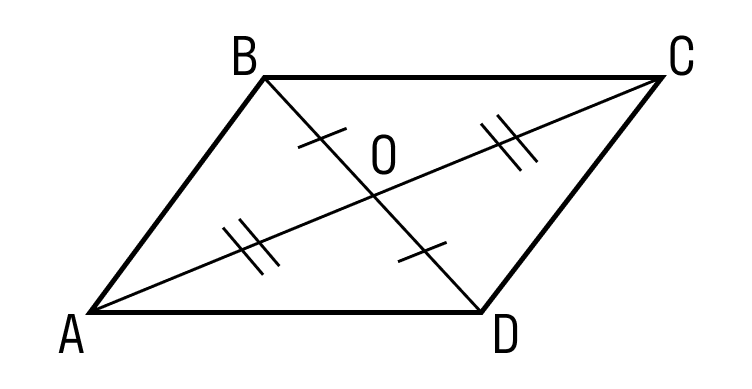
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
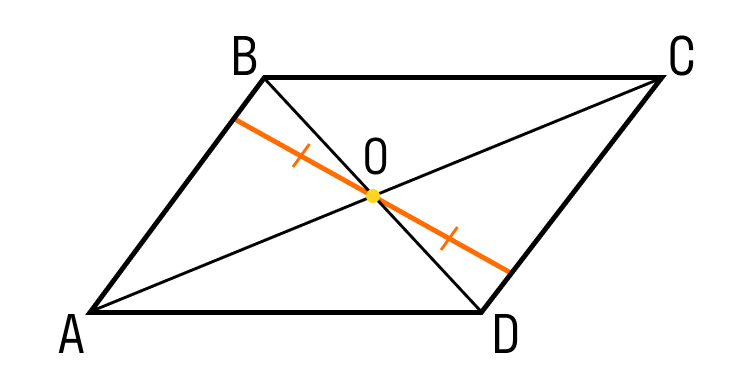
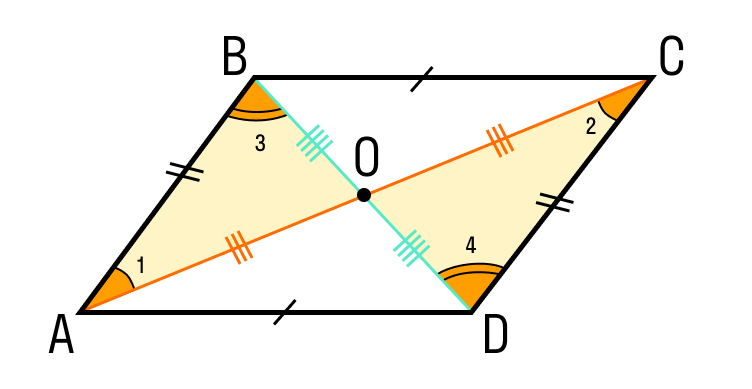
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
- CO = OA;
- DO = BO;
- углы между ними равны, как вертикальные.
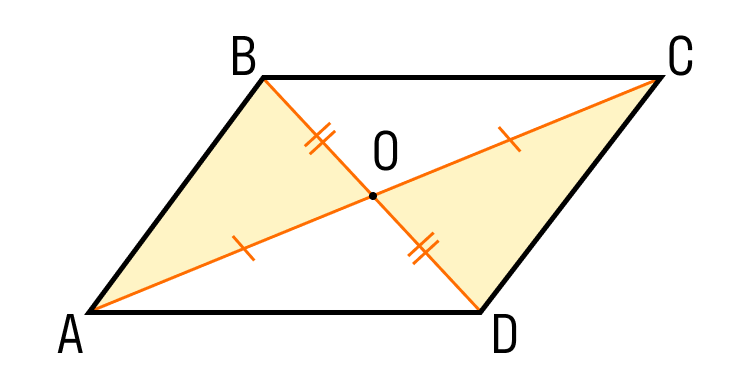
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащиз углов ∠1 = ∠2.
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все таки связано с параллельностью противоположных сторон.
Параллелограмм
Определение
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Теорема (первый признак параллелограмма)
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
Доказательство
Пусть в четырехугольнике (ABCD) стороны (AB) и (CD) параллельны и (AB = CD) .

Проведём диагональ (AC) , разделяющую данный четырехугольник на два равных треугольника: (ABC) и (CDA) . Эти треугольники равны по двум сторонам и углу между ними ( (AC) – общая сторона, (AB = CD) по условию, (angle 1 = angle 2) как накрест лежащие углы при пересечении параллельных прямых (AB) и (CD) секущей (AC) ), поэтому (angle 3 = angle 4) . Но углы (3) и (4) накрест лежащие при пересечении прямых (AD) и (BC) секущей (AC) , следовательно, (ADparallel BC) . Таким образом, в четырехугольнике (ABCD) противоположные стороны попарно параллельны, и, значит, четырехугольник (ABCD) – параллелограмм.
Теорема (второй признак параллелограмма)
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Доказательство
Проведём диагональ (AC) данного четырехугольника (ABCD) , разделяющую его на треугольники (ABC) и (CDA) .

Эти треугольники равны по трем сторонам ( (AC) – общая, (AB = CD) и (BC = DA) по условию), поэтому (angle 1 = angle 2) – накрест лежащие при (AB) и (CD) и секущей (AC) . Отсюда следует, что (ABparallel CD) . Так как (AB = CD) и (ABparallel CD) , то по первому признаку параллелограмма четырёхугольник (ABCD) – параллелограмм.
Теорема (третий признак параллелограмма)
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Доказательство
Рассмотрим четырехугольник (ABCD) , в котором диагонали (AC) и (BD) пересекаются в точке (O) и делятся этой точкой пополам.
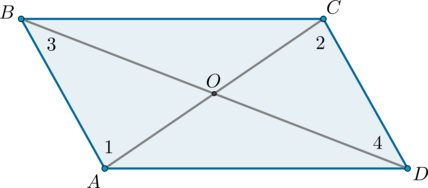
Треугольники (AOB) и (COD) равны по первому признаку равенства треугольников ( (AO = OC) , (BO = OD) по условию, (angle AOB = angle COD) как вертикальные углы), поэтому (AB = CD) и (angle 1 = angle 2) . Из равенства углов (1) и (2) (накрест лежащие при (AB) и (CD) и секущей (AC) ) следует, что (ABparallel CD) .
Итак, в четырехугольнике (ABCD) стороны (AB) и (CD) равны и параллельны, значит, по первому признаку параллелограмма четырехугольник (ABCD) – параллелограмм.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Свойства биссектрисы параллелограмма:
1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.
Доказательство
1) Пусть (ABCD) – параллелограмм, (AE) – биссектриса угла (BAD) .
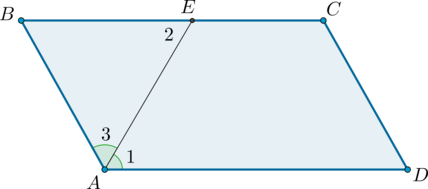
Углы (1) и (2) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (AE) . Углы (1) и (3) равны, так как (AE) – биссектриса. В итоге (angle 3 = angle 1 = angle 2) , откуда следует, что треугольник (ABE) – равнобедренный.
2) Пусть (ABCD) – параллелограмм, (AN) и (BM) – биссектрисы углов (BAD) и (ABC) соответственно.
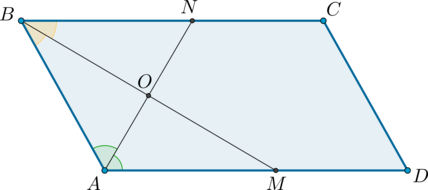
Так как сумма односторонних углов при параллельных прямых и секущей равна (180^
Так как (AN) и (BM) – биссектрисы, то (angle BAN + angle ABM = 0,5(angle DAB + angle ABC) = 0,5cdot 180^circ = 90^
3. Пусть (AN) и (CM) – биссектрисы углов параллелограмма (ABCD) .
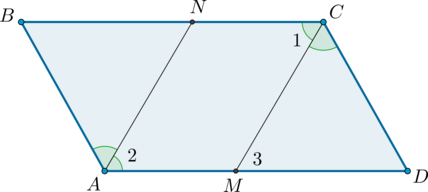
Так как в параллелограмме противоположные углы равны, то (angle 2 = 0,5cdotangle BAD = 0,5cdotangle BCD = angle 1) . Кроме того, углы (1) и (3) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (CM) , тогда (angle 2 = angle 3) , откуда следует, что (ANparallel CM) . Кроме того, (AMparallel CN) , тогда (ANCM) – параллелограмм, следовательно, (AN = CM) .
Параллелограмм
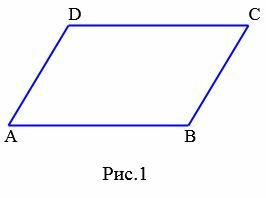
Определение 1. Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны.
На Рис.1 изображен параллелограмм поскольку ( small AB || CD, ;; AD || BC .)
 |
Свойства параллелограмма
Свойство 1. В параллелограмме противоположные углы равны и противоположные стороны равны.
Доказательство. Рассмотрим параллелограмм ABCD (Рис.2).
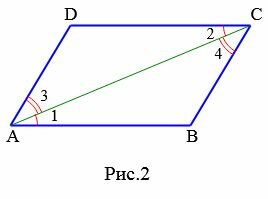 |
Диагональ AC разделяют параллелограмм на два треугольника ACB и ACD. ( small angle 1=angle 2 ) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC (см. теорему 1 статьи Теоремы об углах, образованных двумя параллельными прямыми и секущей). Аналогично ( small angle 3=angle 4 ), если рассмотреть параллельные прямые AD и BC пересеченные секущей AC. Тогда треугольники ACB и ACD равны по одной стороне и двум прилежащим углам: AC общая, ( small angle 1=angle 2 ), ( small angle 3=angle 4 ) (см. статью Треугольники. Признаки равенства треугольников). Поэтому ( small AB=CD, ;; AD=BC, ;; angle B=angle D. )
Из рисунка Рис.2 имеем: ( small angle A=angle 1+angle 3, ;; angle C=angle 2+angle 4. ) Учитывая, что ( small angle 1=angle 2 ) и ( small angle 3=angle 4 ), получим: ( small angle A=angle C. )
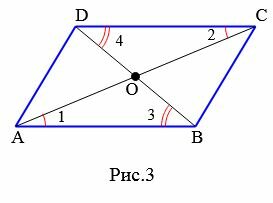
Свойство 2. Диагонали параллелограмма точкой пересечения разделяются пополам.
Доказательство. Рассмотрим параллелограмм ABCD (Рис.3) и пусть O точка пересечения диагоналей AC и BD. ( small angle 1=angle 2 ) поскольку эти углы накрест лежащие, при рассмотрении параллельных прямых AB и CD пересеченные секущей AC. ( small angle 3=angle 4 ), если рассмотреть параллельные прямые AB и CD пересеченные секущей BD. Поскольку в параллелограмме противоположные стороны равны: AB=CD (Свойство 1), то треугольники ABO и CDO равны по стороне и прилежашим двум углам. Тогда AO=OC и BO=OD.
 |
Признаки параллелограмма
Признак 1. Если в четырехугольнике две стороны параллельны и равны, то этот четырехугольник является параллелограммом.
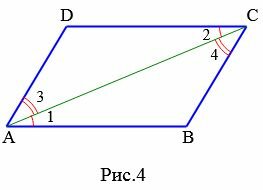 |
Доказательство. Рассмотрим параллелограмм ABCD. Пусть AB=CD и AB || CD. Проведем диагональ AC (Рис.4). Поскольку AB || CD, то ( small angle 1=angle 2 ) как накрест лежащие углы − при рассмотрении параллельных прямых AB и CD пересеченных секущей AC. Тогда треугольники ACB и ACD равны, по двум сторонам и углу между ними. Действительно, AB=CD, AC− общая сторона ( small angle 1=angle 2 ). Но тогда ( small angle 3=angle 4. ) Рассмотрим прямые AD и BC, пересеченные секущей AC. Поскольку ( small angle 3 ) и ( small angle 4 ) являются накрест лежашими углами, то по теореме 1 статьи Параллельные прямые. Признаки параллельности прямых, эти прямые параллельны. Таким образом, в четырехугольнике противоположные стороны попарно параллельны (AB || CD, AD || BC) и, значит, данный четырехугольник параллелограмм. 
Признак 2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник является параллелограммом.
Доказательство. Рассмотрим параллелограмм ABCD (Рис.4). Проведем диагональ AC (Рис.4). Рассмотрим треугольники ACB и ACD. Эти треугольники равны по трем сторонам (см. статью Треугольники. Признаки равенства треугольников). Действительно. AC − общая для этих треугольников и по условию AB = CD, AD = BC. Тогда ( small angle 1=angle 2 ). Отсюда следует AB || CD. Имеем, AB = CD, AB || CD и по признаку 1 четырехугольник ABCD является параллелограммом.
Признак 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения разделяются пополам, то данный четырехугольник − параллелограмм.
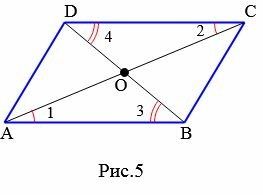 |
Доказательство. Рассмотрим четырехугольник ABCD (Рис.5). Пусть диагонали четырехугольника пересекаются в точке O и точкой пересечения делятся пополам:
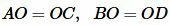 |
Углы AOB и COD вертикальные, следовательно ( small angle AOB=angle COD ). Тогда треугольники AOB и COD равны по двум сторонам и углу меду ними:
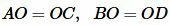 , , 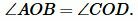 |
Тогда AB = CD и ( small angle 1=angle 2 ). Но по признаку параллельности прямых следует, что AB || CD (теорема 1 статьи Параллельные прямые. Признаки параллельности прямых). Получили:
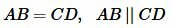 |
и, по признаку 1 четырехугольник ABCD − параллелограмм.
Параллелограмм. Свойства и признаки параллелограмма
Определение параллелограмма
Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.

Свойства параллелограмма

1. Противоположные стороны параллелограмма попарно равны
2. Противоположные углы параллелограмма попарно равны

3. Сумма смежных (соседних) углов параллелограмма равна 180 градусов
4. Сумма всех углов равна 360°
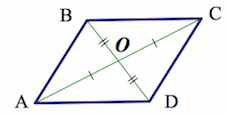 5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам

6. Точка пересечения диагоналей является центром симметрии параллелограмма
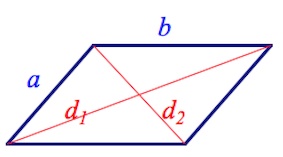
7. Диагонали параллелограмма и стороны
связаны следующим соотношением:

8. Биссектриса отсекает от параллелограмма равнобедренный треугольник
Признаки параллелограмма
Четырехугольник является параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Противоположные стороны попарно равны:
2. Противоположные углы попарно равны:
3. Диагонали пересекаются и в точке пересечения делятся пополам
4. Противоположные стороны равны и параллельны:
5.
Небольшой видеоролик о свойствах параллелограмма (в том числе ромба, прямоугольника, квадрата) и о том, как эти свойства применяются в задачах:
 Формулы площади параллелограмма смотрите здесь.
Формулы площади параллелограмма смотрите здесь.
Хорошую подборку задач на нахождение углов и длин в параллелограмме смотрите здесь.
Признаки параллелограмма, сколько их

Муниципальное общеобразовательное учреждение Гимназия №10
Кировского района г. Волгограда
Региональный фестиваль исследовательских проектов по математике
номинация «секреты разделов математики»
Признаки параллелограмма. Сколько их?
Выполнила: ученица 9 «б» класса
канд. пед. наук, доцент кафедры теории и методики преподавания математики и информатики ВГСПУ
§1. Составление различных пар свойств параллелограмма….…………………….4
§2. Выявление признаков параллелограмма…………………………………………..5
Термин «параллелограмм» греческого происхождения и, согласно Проклу, был введен Евклидом. Понятие параллелограмма и некоторые его свойства были известны еще пифагорейцам. Евклид называл параллелограмм «параллельно-линейной площадью». Слово parallhlogrammou составлено из parallhloz –«параллельный» и grammh – «линия» это слово дало основу для термина «параллелограмм». В дальнейшем Евклид пользовался как существительным. В «Началах» Евклида доказывается следующая теорема: в параллелограмме противоположные стороны равны и противоположные углы равны, а диагональ разделяет его пополам. Евклид не упоминает о том, что точка пересечения диагоналей параллелограмма делит их пополам.
В школьном курсе математики изучаются три признака параллелограмма:
1) Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
2) Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
3) Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Нас заинтересовал вопрос о том, существуют ли еще какие-нибудь признаки параллелограмма. Ведь знание дополнительных признаков позволит упростить решение ряда задач, в которых необходимо установить, что данный в условии четырехугольник является параллелограммом.
Объект исследования – параллелограмм.
Предмет исследования – признаки параллелограмма.
Цель исследования – выявить всевозможные признаки параллелограмма.
· Составить пары различных свойств параллелограмма для выяснения вопроса о том, будут ли они давать признаки параллелограмма.
· Выяснить, какие пары свойств дают признаки параллелограмма и доказать их.
§1. Составление различных пар свойств параллелограмма.
Рассмотрим параллелограмм ABCD, диагонали которого пересекаются в точке O, и перечислим все его свойства.

5)  A=
A= C
C
6)  B=
B= D
D
Каждое из этих свойств, взятое по отдельности, не дает признака параллелограмма. Составим всевозможные пары из этих свойств. Их получилось:
 .
.
Исключим подобные пары. В результате останется 14 пар:
1 и 2 3 и 4 4 и 7 7 и 8
1 и 3 3 и 5 5 и 6
1 и 4 3 и 6 5 и 7
1 и 5 3 и 7 5 и 8
Перед нами возникает задача выяснить, какие из этих пар дают признак параллелограмма, и доказать их. Если же пара свойств не дает признака, то необходимо привести контрпример.
§2. Выявление признаков параллелограмма.

Рассмотрим четырехугольник ABCD, у которого AB || CD и BC || AD. Такой четырехугольник является параллелограммом по определению.
Значит, пара 1 и 2 может рассматриваться как признак параллелограмма.
Данная пара свойств дает признак параллелограмма: если в четырехугольнике две стороны равны и параллельны, то он является параллелограммом. Доказательство этого признака приведено в школьном учебнике, поэтому мы не будем его рассматривать.
Данная пара свойств не дает признака параллелограмма. Контрпримером может служить равнобедренная трапеция.

1 и 5

Рассмотрим четырехугольник ABCD, у которого  A =
A = C и AB || CD. Докажем, что он является параллелограммом.
C и AB || CD. Докажем, что он является параллелограммом.
Поскольку AB||CD, то  ВАС =
ВАС = ACD как накрест лежащие при параллельных прямых. Из равенства этих углов, а также
ACD как накрест лежащие при параллельных прямых. Из равенства этих углов, а также  A и
A и  C следует, что
C следует, что  BCA =
BCA =  DАС. По признаку параллельности прямых получим, что BC||AD. Т. е. ABCD – параллелограмм. Значит, пара 1 и 5 дает признак параллелограмма.
DАС. По признаку параллельности прямых получим, что BC||AD. Т. е. ABCD – параллелограмм. Значит, пара 1 и 5 дает признак параллелограмма.

Рассмотрим четырехугольник ABCD, диагонали которого пересекаются в точке О, и AB||CD, ВО=ОD. Докажем, что он является параллелограммом.
∆ABО = ∆CОD по двум сторонам и углу между ними:
1. ВО = ОD по условию.
2.  АОB =
АОB = DОС как вертикальные.
DОС как вертикальные.
3.  АВО =
АВО = CDО (как накрест лежащие при параллельных прямых).
CDО (как накрест лежащие при параллельных прямых).
Из равенства треугольников следует, что АВ=СD, значит, четырехугольник ABCD является параллелограммом по доказанному выше признаку 1 и 3. Т. е. пара 1 и 7 дает признак параллелограмма.
Данная пара свойств дает признак параллелограмма: если в четырехугольнике противоположные стороны попарно равны, то он является параллелограммом. Доказательство этого признака приведено в школьном учебнике, поэтому мы не будем его рассматривать.
При рассмотрении пар свойств 3 и 5 и 3 и 6 мы столкнулись с вопросом: будут ли равны треугольники по двум сторонам и углу не между ними? Решение этого вопроса мы вынесли в приложение. Здесь же приведем полученные выводы:
1. Если две стороны одного треугольника равны двум сторонам другого треугольника и эти треугольники имеют по равному тупому углу, расположенному не между равными сторонами, то такие треугольники равны.
2. Можно построить два треугольника с данными сторонами а и b и острым углом  , расположенным не между этими сторонами.
, расположенным не между этими сторонами.
Согласно полученным выводам можно привести контрпример для пары свойств 3 и 5. Для этого достаточно построить два различных треугольника со сторонами а и b и углом  не между ними:
не между ними:

Соединив эти треугольники по стороне b, получим такой четырехугольник:


В этом четырехугольнике противолежащие стороны равны и противолежащие острые углы равны, но он не является параллелограммом. Т. е. пара 3 и 5 не дает признак параллелограмма.

Пусть в четырехугольнике АВСD стороны АВ и СD равны и противолежащие тупые углы В и D равны. Тогда треугольники АВС и АСD равны по двум сторонам и тупому углу не между ними. Тогда по доказанному выше признаку АВСD – параллелограмм. Значит, пара 3 и 6 дает признак параллелограмма.
Здесь мы опять сталкиваемся с ситуацией, когда у треугольников АВО и DОС равны две стороны и угол не между ними. Такие треугольники могут оказаться неравными. Чтобы привести контрпример, мы выполнили следующее построение:
1. Нарисовали отрезок ВD и отметили точку О – его середину.
2. Через точку О провели произвольную прямую a.
3. Отложили отрезок ВА, где точка А лежит на прямой a, причем  ВАО – тупой.
ВАО – тупой.
4. Отложили отрезок DС, равный отрезку ВА, с точкой С на прямой а, причем  DСО – острый.
DСО – острый.


В результате получили четырехугольник АВСD, у которого АВ=СD и DО=ОВ, но который не является параллелограммом. Т. е. пара 3 и 7 не дает признак параллелограмма.







Пусть в четырехугольнике АВСD стороны ВС и АD равны и диагональ ВD точкой пересечения с диагональю АС делится пополам. Тогда треугольники ВСО и АОD равны по двум сторонам и тупому углу не между ними. По доказанному выше признаку АВСD – параллелограмм. Значит пара 4 и 7 дает признак параллелограмма.
5 и 6

Пусть дан четырехугольник АВСD, в котором  А=
А= С и
С и  В=
В= D. Докажем, что он является параллелограммом.
D. Докажем, что он является параллелограммом.
Известно, что сумма углов четырехугольника равна 3600, поэтому  . Из равенства углов, данного в условии, получим, что
. Из равенства углов, данного в условии, получим, что  . По признаку параллельности прямых имеем: AB||CD и BC||AD, т. е. АВСD – параллелограмм. Значит, пара 5 и 6 дает признак параллелограмма.
. По признаку параллельности прямых имеем: AB||CD и BC||AD, т. е. АВСD – параллелограмм. Значит, пара 5 и 6 дает признак параллелограмма.



Пусть в четырехугольнике АВСD  А=
А= С и ВО=ОD. Докажем, что он является параллелограммом.
С и ВО=ОD. Докажем, что он является параллелограммом.
Отобразим точку А центрально-симметрично относительно точки О по прямой АС. Пусть при этом она отобразится в точку А1. Если точка А1 совпадает с точкой С, то четырехугольник АВСD является параллелограммом по известному признаку.
Предположим, что точка А1 не совпала с точкой С. Тогда четырехугольник АВА1D является параллелограммом. Значит,  А=
А= А1, а с другой стороны
А1, а с другой стороны  А=
А= С по условию. Тогда
С по условию. Тогда  С=
С= А1, чего быть не может. Мы пришли к противоречию. Следовательно, точка А1 совпадает с точкой С, т. е. АВСD – параллелограмм. Таким образом, пара 5 и 7 дает признак параллелограмма.
А1, чего быть не может. Мы пришли к противоречию. Следовательно, точка А1 совпадает с точкой С, т. е. АВСD – параллелограмм. Таким образом, пара 5 и 7 дает признак параллелограмма.
Эта пара свойств не дает признака параллелограмма. Приведем контрпример:

Данная пара свойств дает признак параллелограмма: если в четырехугольнике диагонали точкой пересечения делятся пополам, то он является параллелограммом. Доказательство этого признака приведено в школьном учебнике, поэтому мы не будем его рассматривать.
Таким образом, из выделенных нами 14 пар свойств 10 пар задают параллелограмм. Пара 1 и 2 может рассматриваться как определение парал – лелограмма, пары 1 и 3, 3 и 4, 7 и 8 изучаются в школе. Еще шесть пар являются признаками параллелограмма, но в школе не изучаются.
Сформулируем полученные признаки:
1. Если в четырехугольнике две стороны параллельны и два противоположных угла равны, то этот четырехугольник – параллелограмм.
2. Если в четырехугольнике две стороны параллельны и одна из диагоналей точкой пересечения делится пополам, то этот четырехугольник – параллелограмм.
3. Если в четырехугольнике две противоположные стороны и два противоположных тупых угла равны, то этот четырехугольник – параллелограмм.
4. Если в четырехугольнике одна из диагоналей точкой пересечения делится пополам и две противоположные большие стороны равны, то этот четырехугольник – параллелограмм.
5. Если в четырехугольнике противоположные углы попарно равны, то этот четырехугольник – параллелограмм.
6. Если в четырехугольнике два противоположных угла равны и одна из диагоналей, не содержащая вершин этих углов, точкой пересечения делится пополам, то этот четырехугольник – параллелограмм.
В результате проведенного исследования нами были открыты и доказаны шесть признаков параллелограмма, которые не рассмотрены в школьных учебниках геометрии.
В процессе доказательства этих признаков мы получили еще один признак равенства треугольников: по двум сторонам и не лежащему между ними тупому углу.
Полученные в работе результаты позволят упростить решение ряда задач на доказательство.
1. Барыбин , 9 -11 кл. – М.: Просвещение, 1974. – 304 с.
2. Геометрия, 7-9: учеб. для общеобразоват. Учреждений / [, , и др.]. – 17-е изд. – М.: Просвещение, 2007. – 384 с.
3. Готман по планиметрии и методы их решения. – М.: Просвещение, 1996. – 240 с.
4. Стройк очерк истории математики. – М., 1984. – 284 с.
5. Шарыгин : 9 – 11 кл.: От учебной задачи к творческой. М., 1996. – 400 с.
6. Семенов геометрию. – М.: Просвещение, 1987. – 256с.
7. Рыбников и развитие математической науки. – М.: Просвещение, 1987. – 159с.
8. Прасолов по планиметрии. – М.: Наука, Гл. ред. физ.-мат. лит., 1986. – 272с.
9. Даан- Пути и лабиринты. Очерки по истории математики. – М.: Мир, 1986. – 432с.
Приложение
Выясним, сколько можно построить треугольников с данными сторонами а и b и углом α, лежащему не между ними. Рассмотрим два случая.
1. Угол α – острый.


Возьмем отрезок АВ и отложим от точки А угол α. Нужно от точки В отложить отрезок длины b, чтобы его конец лежал на стороне угла α. Но можно построить два различных таких отрезка, лежащих по разные стороны от перпендикуляра ВН: ВС и ВD.

Таким образом, если угол α – острый, то существует два треугольника, удовлетворяющих данным условиям.
2. Угол α – тупой.
Действуя также, как в предыдущем случае, получаем, что от точки В можно лишь единственным образом отложить отрезок длины а.
Это дает возможность сформулировать новый признак равенства треугольников: если две стороны одного треугольника равны двум сторонам другого треугольника и эти треугольники имеют по равному тупому углу, расположенному не между равными сторонами, то такие треугольники равны.
Геометрия. Урок 4. Четырехугольники
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение четырехугольника
- Выпуклые четырехугольники
- Параллелограмм
Определение четырехугольника
Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.
Четырехугольники бывают выпуклые ( A B C D ) и невыпуклые ( A 1 B 1 C 1 D 1 ) .
Выпуклые четырехугольники
В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.
Смежные стороны – соседние стороны, которые выходят из одной вершины. Пары смежных сторон: A B и A D , A B и B C , B C и C D , C D и A D .
Противолежащие стороны – несмежные стороны (соединяют разные вершины). Пары противолежащих сторон: A B и C D , B C и A D .
Противолежащие вершины – вершины, не являющиеся соседними (лежат друг напротив друга). Пары противолежащих вершин: A и C , B и D .
Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. A C и B D – диагонали четырехугольника A B C D .
Диагонали выпуклого четырехугольника пересекаются в одной точке.
Площадь произвольного выпуклого четырехугольника можно найти по формуле:
S = 1 2 d 1 d 2 ⋅ sin φ
где d 1 и d 2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).
Рассмотрим более подробно некоторые виды выпуклых четырехугольников.
Класс параллелограммов : параллелограмм, ромб, прямоугольник, квадрат.
Класс трапеций : произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.
Параллелограмм
Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.
Свойства параллелограмма:
- Противолежащие стороны равны.
- Противоположные углы равны.
- Диагонали точкой пересечения делятся пополам.
- Сумма углов, прилежащих к одной стороне, равна 180 ° .
- Сумма квадратов диагоналей равна сумме квадратов сторон. d 1 2 + d 2 2 = 2 ( a 2 + b 2 )
Площадь параллелограмма можно найти по трём формулам.
Как произведение стороны и высоты, проведенной к ней.
Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.
Как произведение двух смежных (соседних) сторон на синус угла между ними.
Как полупроизведение диагоналей на синус угла между ними.
Ромб – параллелограмм, у которого все стороны равны.
Свойства ромба:
- Диагонали пересекаются под прямым углом.
- Диагонали являются биссектрисами углов, из которых выходят.
- Сохраняются все свойства параллелограмма.
Площадь ромба можно найти по трём формулам.
Как произведение стороны ромба на высоту ромба.
Как квадрат стороны ромба на синус угла между двумя сторонами.
Как полупроизведение диагоналей ромба.
Прямоугольник
Прямоугольник – это параллелограмм, у которого все углы равны 90 ° .
Свойства прямоугольника:
- Диагонали прямоугольника равны.
- Сохраняются все свойства параллелограмма.
Площадь прямоугольника можно найти по двум формулам:
Как произведение двух смежных (соседних) сторон прямоугольника.
Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.
Квадрат
Квадрат – прямоугольник, у которого все стороны равны.
Свойства квадрата:
- Сохраняет свойства ромба.
- Сохраняет свойства прямоугольника.
Площадь квадрата можно вычислить по двум формулам:
Как квадрат стороны.
Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).
Трапеция
Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.
Стороны, которые параллельны друг другу называются основаниями , другие две стороны называются боковыми сторонами .
B C и A D – основания, A B и C D – боковые стороны трапеции A B C D .
Свойства трапеции:
сумма углов, прилежащих к боковой стороне, равна 180 ° .
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Средняя линия параллельна основаниям. Её длина находится по формуле: m = a + b 2
Площадь трапеции можно найти по двум формулам:
Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.
Как полупроизведение диагоналей на синус угла между ними.
Виды трапеций
Прямоугольная трапеция – трапеция, у которой два угла прямые.
Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.
Свойство равнобокой трапеции: углы при основании равны
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с четырехугольниками