§ 1. Числовые и алгебраические выражения
В младших классах вы учились оперировать с целыми и дробными числами, решали уравнения, знакомились с геометрическими фигурами, с координатной прямой и координатной плоскостью. Всё это составляло содержание одного школьного предмета «Математика». В действительности такая важная область науки, как математика, подразделяется на огромное число самостоятельных дисциплин: алгебру, геометрию, теорию вероятностей, математический анализ, математическую логику, математическую статистику, теорию игр и т. д. У каждой дисциплины — свои объекты изучения, свои методы познания реальной действительности.
Алгебра, к изучению которой мы приступаем, даёт человеку возможность не только выполнять различные вычисления, но и учит его делать это как можно быстрее, рациональнее. Человек, владеющий алгебраическими методами, имеет преимущество перед теми, кто не владеет этими методами: он быстрее считает, успешнее ориентируется в жизненных ситуациях, чётче принимает решения, лучше мыслит. Наша задача — помочь вам овладеть алгебраическими методами, ваша задача — не противиться обучению, с готовностью следовать за нами, преодолевая возникающие трудности.
На самом деле в младших классах вам уже приоткрыли окно в волшебный мир алгебры, ведь алгебра в первую очередь изучает числовые и алгебраические выражения.

Напомним, что числовым выражением называют всякую запись, составленную из чисел и знаков арифметических действий (составленную, разумеется, со смыслом: например, 3 + 5 • 7 — числовое выражение, тогда как 3 + : — не числовое выражение, а бессмысленный набор символов). По некоторым причинам (о них мы будем говорить в дальнейшем) часто вместо конкретных чисел употребляются буквы (преимущественно из латинского алфавита), тогда получается алгебраическое выражение. Эти выражения могут быть очень громоздкими. Алгебра учит упрощать их, используя разные правила, законы, свойства, формулы.
Пример 1. Найти значение числового выражения

Р е ш е н и е. Сейчас мы вместе с вами кое-что вспомним, и вы увидите, как много алгебраических фактов вы уже знаете.
Прежде всего нужно выработать план осуществления вычислений. Для удобства введём следующие обозначения. Числитель данного дробного выражения обозначим буквой А, а знаменатель — буквой В:
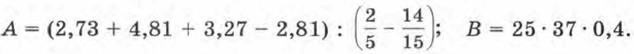
В выражении А обозначим делимое буквой С, а делитель — буквой D. Тогда план наших действий будет выглядеть так:
1) найдём значение с выражения С;
2) найдём значение d выражения D;
3) разделив с на d, найдём значение а выражения А;
4) найдём значение b выражения В;
5) разделив а на b, найдём значение заданного числового выражения.
Итак, план вычислений есть (а наличие плана — половина успеха!), приступим к его реализации.

1) С = 2,73 + 4,81 + 3,27 – 2,81. Конечно, считать подряд или, как иногда говорят, «в лоб»: 2,73 + 4,81, затем к этому числу прибавить 3,27, затем вычесть 2,81. Но культурный человек так вычислять не будет. Он вспомнит переместительный и сочетательный законы сложения (впрочем, ему их и не надо вспоминать, они у него всегда в голове) и будет вычислять так:
(2,73 + 3,27) + (4,81 – 2,81) = 6 + 2 = 8.
2) 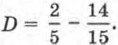 Здесь нам придется вспомнить, как действовать с обыкновенными дробями. Сначала надо привести дроби к общему знаменателю. Наименьшим общим кратным 5 и 15 является число 15, оно и будет общим знаменателем. Для дроби
Здесь нам придется вспомнить, как действовать с обыкновенными дробями. Сначала надо привести дроби к общему знаменателю. Наименьшим общим кратным 5 и 15 является число 15, оно и будет общим знаменателем. Для дроби 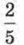 получаем
получаем 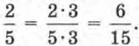 Далее находим
Далее находим
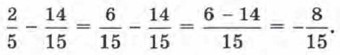
Итак, 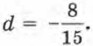
1. Числовые выражения
«Туристы в течение двух часов ехали на велосипедах по шоссе со скоростью 16 км/ч, а затем шли лесом ещё 7 км. Какова длина всего маршрута?»
По шоссе туристы проехали 16-2 км, а лесом прошли 7 км. Поэтому длина всего маршрута равна (16 • 2 + 7) км, т. е. 39 км. Решая задачу, мы получили числовое выражение 16 • 2 + 7. Числовые выражения составляются из чисел с помощью знаков действий и скобок. Приведём ещё примеры числовых выражений:
43 : 5; 9,6 – 3 • 1,2; 5 • (7,4 – 6,1).
Найдём, например, значение выражения 12 • 6 – 35 : 7. Для этого мы должны, соблюдая принятый порядок действий, выполнить сначала умножение и деление, а затем вычитание:
1) 12 • 6 = 72; 2) 35 : 7 = 5; 3) 72 – 5 = 67.
Число 67 — значение выражения 12 • 6 – 35 : 7.
Например, не имеют смысла такие выражения, как

Упражнения
-
Найдите значение выражения:

Выполните действия:

Найдите значение выражения:

Выполните действие:

Выполните действие:

Вычислите:

Найдите:

а) 6; б) 8; в) 3; г) 1.


- Укажите число учащихся, изучающих хотя бы один из этих языков.
- Вычислите число учащихся, изучающих оба языка — английский и немецкий.
- Найдите, сколько процентов учащихся изучают оба языка.
Разряды и классы
Для записи чисел люди придумали десять знаков, которые называются цифрами. Это: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 .
С помощью десяти цифр можно записать любое натуральное число.
От количества знаков (цифр) в числе зависит его название.
Число, состоящее из одного знака (цифры), называется однозначным. Наименьшее однозначное натуральное число — « 1 » , наибольшее — « 9 ».
Число, состоящее из двух знаков (цифр), называется двузначным. Наименьшее двузначное число — « 10 », наибольшее — « 99 » .
Числа, записанные с помощью двух, трёх, четырёх и более цифр, называются двузначными, трёхзначными, четырёхзначными или многозначными. Наименьшее трёхзначное число — « 100 », наибольшее — « 999 ».
Каждая цифра в записи многозначного числа занимает определённое место — позицию.
Разряд — это место (позиция), на котором в записи числа стоит цифра.
Одна и та же цифра в записи числа может иметь разные значения в зависимости от того, в каком разряде она стоит.
Разряды отсчитываются с конца числа.
Разряд единиц — это самый младший разряд, которым заканчивается любое число.
Цифра « 5 » — означает « 5 » единиц, если пятёрка стоит на последнем месте в записи числа (в разряде единиц).

Разряд десятков — это разряд, который стоит перед разрядом единиц.
Цифра « 5 » — означает « 5 » десятков, если она стоит на предпоследнем месте (в разряде десятков).

Разряд сотен — это разряд, который стоит перед разрядом десятков. Цифра « 5 » означает « 5 » сотен, если она стоит на третьем месте от конца числа (в разряде сотен).

Если в числе отсутствует какой-либо разряд, то в записи числа на его месте будет стоять цифра « 0 » (ноль).
Пример. В числе « 807 » содержится 8 сотен, 0 десятков и 7 единиц — такая запись называется разрядным составом числа.
807 = 8 сотен 0 десятков 7 единиц
Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. Например, 10 единиц образуют 1 десяток, а 10 десятков образуют 1 сотню.
Таким образом, значение цифры от разряда к разряду (от единиц к десяткам, от десятков к сотням) увеличивается в 10 раз. Поэтому система счёта (счисления), которую мы используем, называется десятичной системой счисления.
Классы и разряды
В записи числа разряды, начиная справа, группируются в классы по три разряда в каждом.
Класс единиц или первый класс — это класс, который образуют первые три разряда (справа от конца числа): разряд единиц, разряд десятков и разряд сотен.
| Числа | Класс единиц (первый класс) | ||
|---|---|---|---|
| сотни | десятки | единицы | |
| 6 | – | – | 6 |
| 34 | – | 3 | 4 |
| 148 | 1 | 4 | 8 |
| Числа | Класс единиц (первый класс) | ||
|---|---|---|---|
| сотни | десятки | единицы | |
| 6 | – | – | 6 |
| 34 | – | 3 | 4 |
| 148 | 1 | 4 | 8 |
Класс тысяч или второй класс — это класс, который образуют следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч.
| Числа | Класс тысяч (второй класс) | Класс единиц (первый класс) | ||||
|---|---|---|---|---|---|---|
| сотни тысяч | десятки тысяч | единицы тысяч | сотни | десятки | единицы | |
| 5 234 | – | – | 5 | 2 | 3 | 4 |
| 12 803 | – | 1 | 2 | 8 | 3 | |
| 356 149 | 3 | 5 | 6 | 1 | 4 | 9 |
| Числа | Класс тысяч (второй класс) | Класс единиц (первый класс) | ||||
|---|---|---|---|---|---|---|
| сотни тысяч | десятки тысяч | единицы тысяч | сотни | десятки | единицы | |
| 12 803 | – | 1 | 2 | 8 | 3 | |
| 356 149 | 3 | 5 | 6 | 1 | 4 | 9 |
Напоминаем, что 10 единиц разряда сотен (из класса единиц) образуют одну тысячу (единицу следующего разряда: единицу тысяч в классе тысяч).
10 сотен = 1 тысяча
Класс миллионов или третий класс — это класс, который образуют следующие три разряда: единицы миллионов, десятки миллионов и сотни миллионов.
Единица разряда миллионов — это один миллион или тысяча тысяч ( 1 000 тысяч). Один миллион можно записать в виде числа « 1 000 000 ».
Десять таких единиц образуют новую разрядную единицу — десять миллионов «»
Десять десятков миллионов образуют новую разрядную единицу — сто миллионов или в записи цифрами « 100 000 000 ».
| Числа | Класс миллионов (третий класс) | Класс тысяч (второй класс) | Класс единиц (первый класс) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| сотни миллионов | десятки миллионов | единицы миллионов | сотни тысяч | десятки тысяч | единицы тысяч | сотни | десятки | единицы | |
| 8 345 216 | – | – | 8 | 3 | 4 | 5 | 2 | 1 | 6 |
| 93 785 342 | – | 9 | 3 | 7 | 8 | 5 | 3 | 4 | 2 |
| 134 590 720 | 1 | 3 | 4 | 5 | 9 | 7 | 2 | ||
| Числа | Класс миллионов (третий класс) | Класс тысяч (второй класс) | Класс единиц (первый класс) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| сотни миллионов | десятки миллионов | единицы миллионов | сотни тысяч | десятки тысяч | единицы тысяч | сотни | десятки | единицы | |
| 8 345 216 | – | – | 8 | 3 | 4 | 5 | 2 | 1 | 6 |
| 93 785 342 | – | 9 | 3 | 7 | 8 | 5 | 3 | 4 | 2 |
| 134 590 720 | 1 | 3 | 4 | 5 | 9 | 7 | 2 | ||
Как прочитать многозначное число
Чтобы прочитать многозначное число, надо назвать по очереди слева направо число единиц каждого класса и добавить название класса.
Не произносят название класса единиц, а также название класса, все три цифры которого нули.
Например, число « 134 590 720 » читаем: сто тридцать четыре миллиона пятьсот девяносто тысяч семьсот двадцать.
Число « 418 000 547 » читаем: четыреста восемнадцать миллионов пятьсот сорок семь.
На нашем сайте для проверки своих результатов вы можете воспользоваться калькулятором разложения числа на разряды онлайн.
Чтобы легче запомнить, как читать и записывать многозначные числа, советуем использовать выше приведённую «Таблицу классов и разрядов».
Разряды и классы чисел
Классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса:
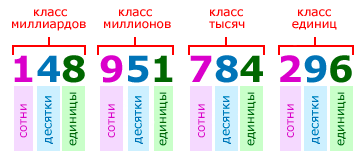
Названия классов многозначных чисел справа налево:
- первый — класс единиц,
- второй — класс тысяч,
- третий — класс миллионов,
- четвёртый — класс миллиардов,
- пятый — класс триллионов,
- шестой — класс квадриллионов,
- седьмой — класс квинтиллионов,
- восьмой — класс секстиллионов.
Для удобства чтения записи многозначного числа, между классами оставляется небольшой пробел. Например, чтобы прочитать число 148951784296, выделим в нём классы:
148 951 784 296
и прочитаем число единиц каждого класса слева направо:
148 миллиардов 951 миллион 784 тысячи 296.
При чтении класса единиц в конце обычно не добавляют слово единиц .
Разряды чисел
Каждая цифра в записи многозначного числа занимает определённое место — позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.
Счёт разрядов идёт справа налево. То есть, первая цифра справа в записи числа называется цифрой первого разряда, вторая цифра справа — цифрой второго разряда и т. д. Например, в первом классе числа 148 951 784 296, цифра 6 является цифрой первого разряда, 9 — цифра второго разряда, 2 — цифра третьего разряда:
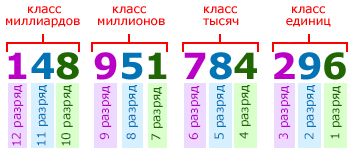
Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами:
- Единицы называют единицами первого разряда (или простыми единицами) и пишутся на первом месте справа.
- Десятки — единицами второго разряда и пишутся в числе на втором месте справа.
- Сотни — единицами третьего разряда и пишутся на третьем месте справа.
- Единицы тысяч — единицами четвёртого разряда и пишутся на четвёртом месте справа.
- Десятки тысяч — единицами пятого разряда и пишутся на пятом месте справа.
- Сотни тысяч — единицами шестого разряда и пишутся в числе на шестом месте справа и так далее.
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Пример. Запишите цифрами число, которое содержит:
1) 37 единиц второго класса и 565 единиц первого класса;
2) 450 единиц второго класса и 9 единиц первого класса;
3) 8 единиц второго класса и 50 единиц первого класса.
Все разрядные единицы, кроме простых единиц, называются составными единицами. Так, десяток, сотня, тысяча и т. д. — составные единицы. Каждые 10 единиц любого разряда составляют одну единицу следующего (более высокого) разряда:
| 10 единиц | = | 1 десяток; |
| 10 десятков | = | 1 сотня; |
| 10 сотен | = | 1 тысяча; |
| 10 тысяч | = | 1 десяток тысяч; |
| 10 десятков тысяч | = | 1 сотня тысяч; |
| 10 сотен тысяч | = | 1 тысяча тысяч (1 миллион); |
Любая составная единица по сравнению с другой единицей, меньшей её называется единицей высшего разряда, а по сравнению с единицей, большей её, называется единицей низшего разряда. Например, сотня является единицей высшего разряда относительно десятка и единицей низшего разряда относительно тысячи.
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, надо отбросить все цифры, означающие единицы низших разрядов и прочитать число, выражаемое оставшимися цифрами.
Например, требуется узнать, сколько всего сотен содержится в числе 6284, т. е. сколько сотен заключается в тысячах и в сотнях данного числа вместе.
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит в числе есть две простые сотни. Следующая влево цифра — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60. Всего, таким образом, в данном числе содержится 62 сотни.
Цифра в каком-нибудь разряде означает отсутствие единиц в данном разряде.
Например, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
24 527 — двадцать четыре тысячи пятьсот двадцать семь.
Многозначные числа. Единицы разрядов и классов. Сумма разрядных слагаемых.
Многозначные числа.
Существуют в математике огромное количество натуральных чисел. Они все разные. Например, 2, 67, 354, 1009. Рассмотрим подробно эти числа.
Натуральное число 2 состоит из одной цифры, поэтому такое число называют, однозначным числом. Еще пример однозначных чисел: 3, 5, 8.
Натуральное число 67 состоит из двух цифр, поэтому такое число называют, двузначным числом. Пример двузначных чисел: 12, 35, 99.
Трехзначные числа состоят из трех цифр, например: 354, 444, 780.
Четырехзначные числа состоят из четырёх цифр, например: 1009, 2600, 5732.
Двузначные, трехзначные, четырехзначные, пятизначные, шестизначные и т.д. числа, называются, многозначными числами.
Разряды чисел.
Рассмотрим число 134. У каждой цифры этого числа есть свое место. Такие места, называются, разрядами.
Цифра 4 занимает место или разряд единиц. Так же цифру 4 можно назвать цифрой первого разряда.
Цифра 3 занимает место или разряд десятков. Или цифру 3 можно назвать цифрой второго разряда.
И цифра 1 занимает разряд сотен. По-другому, цифру 1 можно назвать цифрой третьего разряда. Цифра 1 является последней цифрой слава числа 134, поэтому цифру 1 можно назвать, цифрой высшего разряда. Цифра высшего разряда всегда больше 0.
Каждые 10 единиц любого разряда образуют новую единицу более высокого разряда. 10 единиц образуют один разряд десяток, 10 десятков образуют один разряд сотен, десять сотен образуют разряд тысяч и т.д.
Если нет какого-то разряда, то вместо него будет стоять 0.
Например: число 208.
Цифра 8 – первый разряд единиц.
Цифра 0 – второй разряд десятков. 0 означает в математике ничего. Из записи следует, что десятков у данного числа нет.
Цифра 2 – третий разряд сотен.
Такой разбор числа называется разрядным составом числа.
Классы.
Многозначные числа разбивают на группы по три цифры справа налево. Такие группы цифр называют классам. Первый класс справа называется классом единиц, второй называется классом тысяч, третий – классом миллионов, четвёртый – классом миллиардов, пятый – классом триллионов, шестой – классом квадриллионов, седьмой – классом квинтиллионов, восьмой – классом секстиллионов.
Класс единиц – первый класс справа с конца три цифры состоит из разряда единиц, разряда десятков и разряда сотен.
Класс тысяч – второй класс состоит из разряда: единиц тысяч, десятков тысяч и сотен тысяч.
Класс миллионов – третий класс состоит из разряда: единиц миллионов, десятков миллионов и сотен миллионов.
Разберем пример:
У нас есть число 13 562 006 891.
Это число имеет 891 единиц в классе единиц, 6 единиц в классе тысяч, 562 единиц в классе миллионов и 13 единиц в классе миллиардов.
Таблица разрядов и классов.
Чтобы прочитать натуральное число 13562006891 нужно справа отметить по три цифры класса 13 562 006 891 и прочитать число единиц каждого класса слева направо:
 13 миллиардов 562 миллионов 6 тысяч 891.
13 миллиардов 562 миллионов 6 тысяч 891.
Сумма разрядных слагаемых.
Любое натурально число имеющее различные разряды можно разложить на сумму разрядных слагаемых. Рассмотрим пример:
Число 4062 распишем на разряды.
4 тысяч 0 сотен 6 десятков 2 единиц или по-другому можно записать
4062=4 ⋅1000+0 ⋅100+6 ⋅10+2
Следующий пример:
26490=2 ⋅10000+6 ⋅1000+4 ⋅100+9 ⋅10+0
Вопросы по теме:
Назовите первые четыре класса в записи натуральных чисел?
Ответ: класс единиц, класс тысяч, класс миллионов, класс миллиардов.
Как читают многозначные числа?
Ответ: многозначные числа читают слева направо. Разбивают число по 3 цифры с конца на классы, называют все цифры, кроме нуля. Цифра 0 в записи числа означают отсутствие разряда.
Какие цифры могут стоять в любом разряде числа, кроме высшего?
Ответ: 0, 1, 2, 3, 4. 5, 6, 7, 8, 9.
Какие цифры могут стоять в высшем разряде числа?
Ответ: 1, 2, 3, 4. 5, 6, 7, 8, 9.
Что такое сумма разрядных слагаемых?
Ответ: Это разложение натурального числа на разряды и суммирование их.
Сколько десятков в сотне?
Ответ: в сотне 10 десятков.(10+10+10+10+10+10+10+10+10+10=100)
Сколько сотен в тысячи?
Ответ: в тысячи 10 сотен. (100+100+100+100+100+100+100+100+100+100=1000)
Сколько десятков в тысячи?
Ответ: в тысячи 100 десятков.
Сколько тысяч в миллионе?
Ответ: в миллионе 1000 тысяч.
Примеры на задачи.
Пример №1:
Запишите и прочитайте число: а) пятизначное б) шестизначное.
Ответ: а) 35 100 (тридцать пять тысяч сто) б) 803 273 (восемьсот три тысячи двести семьдесят три)
Пример №2:
Сколько натуральных чисел: а) однозначных б) двузначных?
Ответ: а) однозначных натуральных чисел 10 (0, 1, 2, 3, 4. 5, 6, 7, 8, 9), б) двузначных натуральных чисел 90 (10, 11, 12, …,99)
Пример №3:
В записи числа 10398 назовите цифры разрядов единиц, десятков, сотен, тысяч, десятков тысяч, …
Ответ: 8 – разряд единиц, 9 – разряд десятков, 3 – разряд сотен, 0 – разряд тысяч, 1 – разряд десятков тысяч.
Пример №4:
Напишите наименьшее трехзначное число и наибольшее пятизначное число.
Ответ: 100 и 99999.
Пример №5:
Запишите число 56976 в виде суммы разрядных слагаемых:
Ответ: 56976=50000+6000+900+70+6=5⋅10000+6⋅1000+9⋅100+7⋅10+6
Разряды и классы чисел

О чем эта статья:
Числа и цифры
Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.
Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
- Единица (1) — самое маленькое число, а самого большого числа не существует.
- Ноль (0) означает, что предмета нет. Ноль не является натуральным числом.
От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.
Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определенное место — позицию.
Классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.

Названия классов многозначных чисел справа налево:
- первый — класс единиц,
- второй — класс тысяч,
- третий — класс миллионов,
- четвертый — класс миллиардов,
- пятый — класс триллионов,
- шестой — класс квадриллионов,
- седьмой — класс квинтиллионов,
- восьмой — класс секстиллионов.
Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
- 125 911 723 296.
А теперь прочитаем число единиц каждого класса слева направо:
- 125 миллиардов 911 миллионов 723 тысячи 296.
Разряды чисел
От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
- 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу.
Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.
Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.

Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще чтобы визуально разделить классы чисел.
Разрядные единицы обозначают так:
- Единицы — единицами первого разряда (или простыми единицами) и пишут на первом месте справа.
- Десятки — единицами второго разряда и записывают в числе на втором месте справа.
- Сотни — единицами третьего разряда и записывают на третьем месте справа.
- Единицы тысяч — единицами четвертого разряда и записывают на четвертом месте справа.
- Десятки тысяч — единицами пятого разряда и записывают на пятом месте справа.
- Сотни тысяч — единицами шестого разряда и записывают в числе на шестом месте справа и так далее.
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Чтобы легче понимать математику — записывайтесь на наши онлайн-курсы по математике!
Потренируемся
Пример 1. Записать цифрами число, в котором содержится:
- 55 единиц второго класса и 100 единиц первого класса;
- 110 единиц второго класса и 5 единиц первого класса;
- 7 единиц второго класса и 13 единиц первого класса.
- 55 100;
- 110 005;
- 7 013.
Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
- 10 единиц равны 1 десятку;
- 10 десятков равны 1 сотне;
- 10 сотен равны 1 тысяче;
- 10 тысяч равны 1 десятку тысяч;
- 10 десятков тысяч равны 1 сотне тысяч;
- 10 сотен тысяч равны 1 миллиону.
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.
Пример 2. Сколько сотен содержится в числе 6284?
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.
Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.
Значит, в данном числе содержится 62 сотни.
Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.
Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
- 11 627 — одиннадцать тысяч шестьсот двадцать семь.
- 31 502 — тридцать одна тысяча пятьсот два.
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.
4 класс. Математика. Чтение и запись многозначных чисел.
4 класс. Математика. Чтение и запись многозначных чисел.
- Оглавление
- Занятия
- Обсуждение
- О курсе
Вопросы
Поделись с друзьями
Комментарии преподавателя
Данный урок поможет получить представление о теме «Чтение многозначных чисел», которая входит в школьный курс математики 4 класса. Учитель расскажет о том, как правильно читать многозначные числа, состоящие из тысяч, и как правильно записывать такие числа при помощи цифр.
Введение, знакомство с новым классом – классом тысяч
Если предметов много, то при счете используют не только знакомые вам счетные единицы: единицы, десятки, сотни – но и более крупные, например тысячи. Тысячи считают так же, как и простые единицы: одна тысяча, две тысячи, три тысячи, четыре тысячи и так далее.
Десять тысяч – это один десяток тысяч.
Десять десятков тысяч – это одна сотня тысяч.
Десять сотен тысяч – это тысяча тысяч, или миллион.
Составим таблицу классов и разрядов (рис. 1).

Рис. 1. Таблица классов и разрядов
Вы знаете, что единицы, десятки, сотни составляют класс единиц, или первый класс. Единицы тысяч, десятки тысяч и сотни тысяч составляют класс тысяч, или второй класс. Еще раз посмотрите на таблицу: сколько разрядов в каждом классе? Проверьте: три разряда. Разряды первого класса: единицы, десятки, сотни. Разряды второго класса: единицы тысяч, десятки тысяч и сотни тысяч.
Чтобы прочитать многозначное число, его разбивают на классы, отсчитывая справа по три цифры, затем считают, сколько единиц каждого класса, начиная с высшего.
Пример
2 класс – класс тысяч
1 класс – класс единиц
1. 
Три нуля в записи показывают отсутствие единиц первого класса. Название класса единиц не произносится. Читаем число с высшего класса: «триста семьдесят две тысячи».
2. 
В этом числе мы видим 145 единиц второго класса и 312 единиц первого класса. Читаем число с высшего класса: «сто сорок пять тысяч триста двенадцать».
3. 
В этом числе 528 единиц второго класса и 609 единиц первого класса. Читаем число: «пятьсот двадцать восемь тысяч шестьсот десять».
4. 
В данном числе 60 единиц второго класса и 500 единиц первого класса. Это «шестьдесят тысяч пятьсот».
5. 
В последнем числе 7 единиц второго класса и 4 единицы первого класса. Число «семь тысяч четыре».
Задание 1
Разбейте число на классы. Скажите, сколько в нем единиц каждого класса.
Отсчитаем справа у каждого числа три цифры.
1. 
В числе 5 единиц второго класса и 400 единиц первого класса. Читаем: «пять тысяч четыреста».
2. 
В числе 5 единиц второго класса и 432 единицы первого класса. Читаем: «пять тысяч четыреста тридцать два».
3.
В числе 61 единица второго класса и 209 единиц первого класса. Читаем: «шестьдесят одна тысяча двести девять».
4. 
В числе 61 единица второго класса и 290 единиц первого класса. Читаем: «шестьдесят одна тысяча двести девяносто».
5. 
В числе 500 единиц второго класса и 500 единиц первого класса. Читаем: «пятьсот тысяч пятьсот».
6. 
В числе 500 единиц второго класса и 5 единиц первого класса. Читаем: «пятьсот тысяч пять».
Задание 2
Запишите цифрами числа:
1. Сто восемь тысяч триста девять
2. Тридцать тысяч семьсот девять
3. Восемь тысяч шестьсот
Многозначные числа записывают по классам, начиная с высшего. Чтобы записать цифрами число, например «сто восемь тысяч триста девять», сначала записывают, сколько всего единиц второго, высшего, класса в числе – 108, потом записывают, сколько всего единиц первого класса в числе.
Для числа «тридцать тысяч семьсот семьдесят» запишем количество единиц второго высшего класса в числе, их тридцать, и количество единиц первого класса в числе, семьсот семьдесят.
В числе «восемь тысяч шестьсот» 8 единиц второго класса и шестьсот единиц первого класса.
2 класс – класс тысяч
1 класс – класс единиц
Задание 3
Прочитайте по-разному числа: 3754, 2900, 3970.
3754. Это число можно прочитать по-разному:
Название класса единиц обычно не произносится, поэтому прочитаем так: три тысячи семьсот пятьдесят четыре.
Б) 3 тыс. 7 сот. 5 дес. 4 ед.
Мы назвали количество единиц каждого разряда.
В) 37 сот. 5 дес. 4 ед.
Е) 3 тыс. 75 дес. 4 ед.
А) 3 тыс. 9 сот. 7 дес.
В) 3 тыс. 9 сот. 70 ед.
Свойство
Число, в котором есть единицы разных разрядов, можно заменить суммой разрядных слагаемых.
Задание 4
Замените суммой разрядных слагаемых числа:
1903: 1 тыс. 9 сот. 3 ед.

407 020: 4 сот. тыс. 0 дес. тыс. 7 ед. тыс. 0 сот. 2 дес. 0 ед.

300 206: 3 сот. тыс. 0 дес. тыс. 0 ед. тыс. 2 сот. 0 дес. 6 ед.

164 800: 1 сот. тыс. 6 дес. тыс. 4 ед. тыс. 8 сот. 0 дес. 0 ед.

Замечание: если в разряде стоит ноль, его можно не писать, так как при прибавлении нуля получается то же число.
Если натуральное число состоит из одного знака – одной цифры, то его называют однозначным, например, числа 3, 5, 9 – однозначные.
сли число состоит из двух знаков – двух цифр, то его называют двузначным. Например, числа 10, 23, 75 – двузначные.
Так же по числу знаков в данном числе дают названия и другим числам. Например: 145, 809 – это трехзначные числа.
Существуют четырехзначные, пятизначные числа и так далее.
Двузначные, трехзначные и так далее числа называют многозначными.
 Для чтения многозначное натуральное число разбивают справа налево на группы по три цифры в каждом (самая левая группа может состоять из одной или двух цифр). Эти группы называют классами. Каждая из трех цифр класса обозначает разряд: разряд единиц, разряд десятков, разряд сотен.
Для чтения многозначное натуральное число разбивают справа налево на группы по три цифры в каждом (самая левая группа может состоять из одной или двух цифр). Эти группы называют классами. Каждая из трех цифр класса обозначает разряд: разряд единиц, разряд десятков, разряд сотен.
Классификация начинается справа. Три первые цифры справа составляют класс единиц, три следующие – класс тысяч, далее идет класс миллионов, затем – миллиардов. (см. Рис.). Так как ряд натуральных чисел бесконечен, то за миллиардами идут триллионы, за триллионами — триллиарды и т.д.
 Миллион – это тысяча тысяч, его записывают с помощью единицы и шести нулей.
Миллион – это тысяча тысяч, его записывают с помощью единицы и шести нулей.
 Миллиард – это тысяча миллионов. Его записывают с помощью единицы и 9 нулей.
Миллиард – это тысяча миллионов. Его записывают с помощью единицы и 9 нулей.
Как же правильно прочитать многозначное число? Начинают читать многозначное число слева направо, по очереди называют число единиц каждого класса и добавляют название класса. При этом название класса единиц не называют, как и класса, в котором все три цифры — нули.
Например, вот это число (42 135 308) разбивают на классы так: оно имеет 308 единиц, 135 единиц в классе тысяч, 42 единицы в классе миллионов. Поэтому читают его так: 42 миллиона 135 тысяч 308.
Любое натуральное число можно представить в виде суммы разрядных единиц.
32 537 = 30 000 + 2 000 + 500 + 30 + 7
Таким образом, в этом уроке Вы познакомились с понятием натурального числа и натурального ряда, научились читать и классифицировать натуральные многозначные числа, а также раскладывать их по разрядам.
Источник конспекта:: http://interneturok.ru/ru/school/matematika/4-klass/tema-3/chtenie-mnogoznachnyh-chisel?konspekt
Источник видео: http://www.youtube.com/watch?v=frHwo0rvmvM
Файлы
Нет дополнительных материалов для этого занятия.





