Формулы площадей всех фигур

Формулы площади

Площадь геометрической фигуры – часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади выражается числом заключающихся в него квадратных единиц.

Формулы площади треугольника

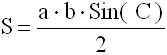
S – площадь треугольника

a, b – длины 2-х сторон треугольника

С – угол между сторонами a и b

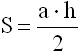
S – площадь треугольника

a – длина стороны треугольника

h – длина высоты, опущенной на сторону a

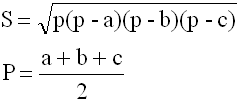
S – площадь треугольника

a, b, c – длины 3-х сторон треугольника

p – полупериметр треугольника

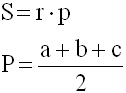
S – площадь треугольника

r – радиус вписанной окружности

p – полупериметр треугольника

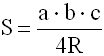
S – площадь треугольника

a, b, c – длины 3-х сторон треугольника

R – радиус описанной окружности

Формулы площади квадрата:

1) Площадь квадрата равна квадрату длины его стороны (a).

2) Площадь квадрата равна половине квадрата длины его диагонали (d).

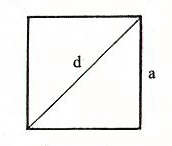
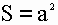
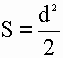
S – площадь квадрата

a – длина стороны квадрата

d – длина диагонали квадрата

Формула площади прямоугольника:

1) Площадь прямоугольника равна произведению длин двух его смежных сторон (a, b).

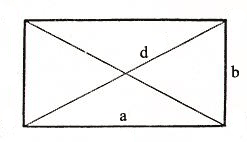
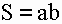
S – площадь прямоугольника

a – длина 1-ой стороны прямоугольника

b – длина 2-ой стороны прямоугольника

Формула площади параллелограмма:

1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).

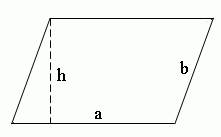
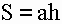
S – площадь параллелограмма

a – длина основания

h – длина высоты

Формула площади трапеции:

1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).

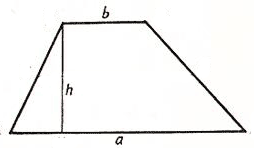
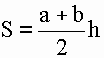
S – площадь трапеции

a – длина 1-ого основания

b – длина 2-ого основания

h – длина высоты трапеции

Формулы площади ромба:

1) Площадь ромба равна произведению длины его стороны на высоту (a, h).

2) Площадь ромба равна половине произведения его диагоналей.

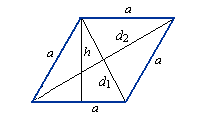
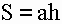
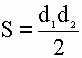
S – площадь ромба

a – длина основания ромба

h – длина высоты ромба

d₁ – длина 1-ой диагонали

d₂ – длина 2-ой диагонали

Формула площади круга:

1) Площадь круга равна произведению квадрата радиуса на число пи (3.1415).

2) Площадь круга равна половине произведения длины ограничивающей его окружности на радиус.

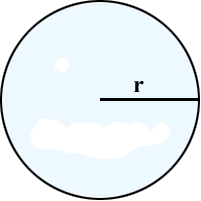
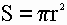
S – площадь круга

π – число пи (3.1415)

r – радиус круга

Формула площади эллипса:

1) Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи (3.1415).

Площади фигур. Основные формулы.

Площадь треугольника.

а – основание, h – высота, проведенная к этому основанию.

Формула применима для любого треугольника.

a, b – стороны, α – угол между этими сторонами.

Формула применима для любого треугольника.

a, b, с – стороны, р – полупериметр (сумма трех сторон, деленная пополам).

Формула применима для любого треугольника.

r – радиус вписанной в треугольник окружности, р – полупериметр (сумма трех сторон, деленная пополам).

Формула применима для любого треугольника.

a, b, с – стороны, R – радиус описанной около треугольника окружности, d – диаметр описанной окружности.

Формула применима для любого треугольника.

R – радиус описанной около треугольника окружности, α, β, γ – углы треугольника.

Формула применима для любого треугольника.

Формула применима для прямоугольного треугольника.

Формула применима для равностороннего (правильного) треугольника.

Площадь квадрата и прямоугольника.

Формула	Рисунок	Расшифровка формулы
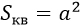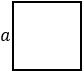		а – сторона квадрата
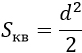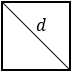		d – диагональ квадрата
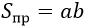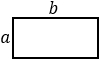		a, b – стороны прямоугольника
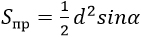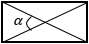		d – диагональ прямоугольника, α – угол между диагоналями (угол можно брать и острый, и тупой, т.к. синусы смежных углов равны)

Площадь параллелограмма и ромба.

Формула	Рисунок	Расшифровка формулы
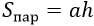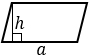		а – одна из сторон параллелограмма, h – высота, проведенная к этой стороне
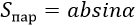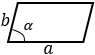		а, b – стороны параллелограмма, α – угол между этими сторонами
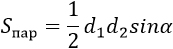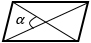		d1, d2 – диагонали, α – угол между диагоналями (можно брать любой угол, т.к. синусы смежных углов равны)
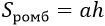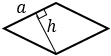		а – сторона ромба, h – высота, проведенная к этой стороне
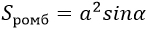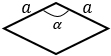		а – сторона ромба, α – угол между этими сторонами
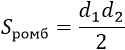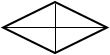		d1, d2 – диагонали ромба

Площадь трапеции.

а, b – основания трапеции, h – высота.

Формула применима для любой* трапеции.

m – средняя линия трапеции, h – высота.

Формула применима для любой трапеции.

d 1 , d 2 – диагонали трапеции, α – угол между диагоналями (можно брать любой угол, т.к. синусы смежных углов равны).

Формула применима для любой трапеции.

*Любая трапеция – это и равнобедренная, и прямоугольная, и тупоугольная, и произвольная

Площадь круга и кругового сектора.

Формула	Рисунок	Расшифровка формулы
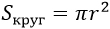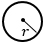		r – радиус
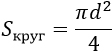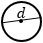		d – диаметр
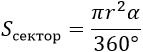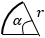		r – радиус, α – угол кругового сектора
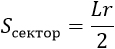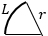		r – радиус, L – длина дуги кругового сектора

Площадь многоугольника.

р – полупериметр (сумма всех сторон многоугольника, деланная на 2), r – радиус вписанной в этот многоугольник окружности.

*Пятиугольник нарисован для примера.

Формула работает как для правильного, так и для произвольного многоугольника, главное, чтобы в него можно было вписать окружность.

Геометрия

План урока:

Теорема Пифагора

Попытаемся установить связь между гипотенузой и катетами прямоугольного треугольника. Пусть в некотором прямоугольном треуг-ке катеты имеют длины а и b, а гипотенуза равна с. Пусть один из острых углов треуг-ка составляет α, тогда другой острый угол должен равняться 90 – α:

Далее возьмем 4 таких треуг-ка и расположим их следующим образом:

Здесь мы прикладываем треуг-ки так, чтобы их разные катеты образовали одну сторону четырехугольника. В результате получается большой квадрат со стороной a + b. Квадратом он является по определению, ведь все его стороны одинаковы, а углы – прямые.

Изучим центральную фигуру, чью площадь мы обозначили как S₂. Это четырехуг-к, причем все его стороны равны с, то есть длине гипотенузы треугольника. С другой стороны, каждый его угол можно найти, вычтя из 180° величины α и 90° – α:

Получается, что всего его углы прямые, то есть он является квадратом. Найдем его площадь:

Вернемся к большому квадрату. С одной стороны, его площадь можно записать как сумму площадей фигур, его составляющих:

Cдругой стороны, эту же площадь можно найти, просто возведя в квадрат его сторону:

Получили формулу, в которой и заключен смысл теоремы Пифагора:

Изучим несколько простейших примеров использования теоремы Пифагора.

Задание. Длины катетов прямоугольного треугольника составляют 5 и 12. Определите длину гипотенузы.

Решение. Запишем теорему Пифагора:

Задание. Длина катета треугольника составляет 3, а гипотенузы – 5. Какова длина другого катета?

Решение: На это раз нам известен один из катетов а = 3 и гипотенуза с = 5. Подставим в теорему Пифагора эти числа:

Теорема Пифагора имеет огромное значение для геометрии и смежных дисциплин. Приведенное здесь ее доказательство является одним из простейших, но отнюдь не единственным. Сегодня человечеству известно 367 различных доказательств теоремы Пифагора, что лишь показывает ее огромную значимость.

На самом деле Пифагор, известный древнегреческий математик, не был первым, кто обнаружил это равенство. Пифагор родился примерно в 570 г. до н. э., однако ещё египтяне знали про прямоугольный треуг-к со сторонами 3, 4 и 5. Поэтому его часто именуют египетским треугольником.

Также вычислять стороны прямоугольного треуг-ка умели и в Вавилоне уже за 1000 лет до рождения Пифагора. Вероятно, Пифагор узнал о формуле от вавилонян, а сам лишь вывел ее доказательство (вавилоняне не утруждали себя необходимостью доказывать теоремы геометрии). Утверждается, что Пифагор принес сделал жертвоприношение в размере 100 быков после того, как смог доказать теорему.

Задание. Вычислите гипотенузу равнобедренного прямоугольного треуг-ка, чьи катеты имеют единичную длину.

Решение. В теорему Пифагора вместо букв a и b подставим единицу:

Обратите внимание, что в данной задаче в качестве длины гипотенузы прямоугольного треугольника получилось иррациональное число. Исторически именно при решении подобной задачи люди (это были ученики Пифагора) впервые столкнулись с иррациональными числами. Перед дальнейшим изучением темы есть смысл вспомнить основные правила вычислений с квадратными корнями.

Задание. На рисунке построен произвольный квадрат. Предложите способ, как построить квадрат с вдвое большей площадью.

Решение. Проведем в исходном квадрате диагональ. Далее построим новый квадрат со стороной, равной этой гипотенузе:

Докажем, что получившийся квадрат (его стороны отмечены синим цветом) вдвое больше исходного квадрата. Пусть сторона изначального квадрата равна х.Тогда его площадь составляет х 2 . Диагональ разбивает квадрат на два прямоугольных треуг-ка, в которых она является гипотенузой.

Запишем для одного из них теорему Пифагора:

Но площадь квадрата равна его стороне, возведенной во вторую степень, поэтому величина с 2 – это площадь большого (на рисунке – синего)квадрата, а х 2 – площадь маленького:

Подставим эти выражения в формулу, выведенную из теоремы Пифагора, и получим, что площадь большего квадрата ровно вдвое больше:

Задание. Найдите площадь равнобедренного прямоугольного треуг-ка, гипотенуза которого имеет длину 10.

Решение. Обозначим катеты переменной х, тогда теорема Пифагора будет выглядеть как уравнение:

Задание. Один из острых углов прямоугольного треугольника составляет 30°, а его гипотенуза равна 10. Найдите оба катета.

Решение. Мы знаем, что в прямоугольном треуг-ке с острым углом 30° гипотенуза вдвое длиннее меньшего катета (он как раз лежит против угла 30°), мы можем найти этот катет:

Другой катет находим с помощью теоремы Пифагора:

Задачи на применение теоремы Пифагора

Теорема Пифагора используется в огромном количестве геометрических задач. С ее помощью можно находить диагонали некоторых четырехуг-ков, длины высот, вычислять площади.

Задание. Стороны прямоуг-ка имеют длину 8 и 15 см. Найдите длину его диагонали.

Решение. Рассмотрим произвольный прямоугольник АВСD. Если в нем провести диагональ ВD, то получится прямоугольный треуг-к АВD. Пусть АВ = 15, АD = 8. Запишем теорему Пифагора для ∆АВD:

Задание. В равнобедренном треуг-ке основание имеет длину 16 см, а боковые стороны составляют 17 см. Найдите длину высоты, проведенной к основанию этого треуг-ка, а также площадь треуг-ка.

Решение. Напомним, что высота, опущенная к основанию равнобедренного треуг-ка, одновременно является и медианой, и биссектрисой. Это значит, что Н – середина АВ. Тогда можно найти длину отрезков АН и НВ:

Теперь можно рассмотреть ∆АСН. Он прямоугольный, и нам известно его гипотенуза (она является боковой стороной ∆АВС и по условию равна 17 см) и катет АН. Тогда можно найти и второй катет, то есть высоту СН:

Задание. Высота равностороннего треуг-ка составляет 4 см. Найдите его сторону.

Решение. Напомним, что в равностороннем треуг-ке все углы равны 60°. Также учтем, что высота в равностороннем треуг-ке является также и биссектрисой и медианой:

Рассмотрим ∆АСН. Он прямоугольный, и один из его углов составляет 60°. Значит, другой угол составляет 30°. Но в таком треуг-ке гипотенуза вдвое больше катета, лежащего против ∠30°:

Обратите внимание, мы специально домножили дробь на корень из 3, чтобы корень оказался в числителе, а не знаменателе. Т.к. в таком виде проще работать с квадратными корнями.

Итак, мы нашли АН. Теперь можно найти сторону АС, которая вдвое длиннее:

Задание. Составьте формулу для нахождения площади равностороннего треуг-ка, если известна только его сторона.

Решение. Обозначим сторону треуг-ка буквой а. Для вычисления площади необходимо найти высоту:

Как и в предыдущей задаче, отрезок АС вдвое длиннее АН:

Высоту мы нашли. Осталось найти площадь:

Задание. В прямоугольном треуг-ке, катеты которого имеют длину 60 и 80, проведена высота к гипотенузе. Найдите высоту гипотенузы, а также длину отрезков, на которые эта высота разбивает гипотенузу.

Решение. Найдем длину гипотенузы ВС:

Осталось найти длины отрезков СН и НВ. Для этого необходимо записать теорему Пифагора для ∆АСН и ∆АНВ, которые являются прямоугольными. Начнем с ∆АСН:

Аналогично работаем и с ∆АНВ:

Можно проверить себя. Отрезки НВ и СН вместе составляют отрезок СВ, поэтому должно выполняться равенство:

Задание. Диагонали ромба равны 10 и 24 см. Чему равна его сторона?

Пусть в ромбе АВСD диагонали пересекаются в точке О, причем АС = 24 см, а ВD = 10 см.Напомним, что диагонали ромба пересекаются под углом 90° и делятся при этом на одинаковые отрезки. Следовательно, ∆АВО прямоугольный. Найдем его катеты:

Задание. Основания равнобедренной трапеции имеют длину 20 и 10, а боковая сторона имеет длину 13. Найдите площадь трапеции.

Решение. Опустим на большее основание две высоты:

В итоге получили прямоуг-к АВКН. Его противоположные стороны одинаковы, поэтому

∆АНD и ∆ВКС равны друг другу, ведь это прямоугольные треуг-ки с одинаковой гипотенузой (АD = ВС, ведь это равнобедренная трапеция) и равным катетом (АН = ВК как стороны прямоуг-ка). Это значит, что DH = КС. Но эти отрезки вместе с НК составляют CD. Это позволяет найти DH и KC:

Зная высоту трапеции и ее основания, легко найдем и ее площадь:

Пифагоровы тройки

Возможно, вы уже заметили, что в большинстве школьных задач на применение теоремы Пифагора используются треуг-ки с одними и теми же сторонами. Это треуг-к, чьи стороны имеют длины

Их использование обусловлено тем, что все их стороны выражаются целыми числами. В задачах же, например, с равнобедренным прямоугольным треуг-ком хотя бы одна из сторон обязательно оказывается иррациональным числом.

Прямоугольные треуг-ки, у которых все стороны являются целыми, называют пифагоровыми треугольниками, а длины их сторон именуются пифагоровыми тройками. Получается, что пифагоровыми называются такие тройки натуральных чисел а, b и с, которые при подстановке в уравнение

обращают его в справедливое равенство.

Для удобства такие тройки иногда записывают в скобках.

Например, тройка чисел (3; 4; 5)– пифагорова, так как

Задание. Определите, какие из следующих троек чисел являются пифагоровыми:

Несложно догадаться, что пифагоровых троек существует бесконечно много. Действительно, возьмем тройку (3; 4; 5). Далее умножим все числа, составляющие ее, на два, и получим новую тройку (6; 8; 10), которая также пифагорова. Умножив исходную тройку на 3, получим тройку (9; 12; 15), и она снова пифагорова. Вообще, умножая числа пифагоровой тройки на любое натуральное число, всегда будем получать новую пифагорову тройку. А так как натуральных чисел бесконечно много, то и троек Пифагора также бесконечное количество.

Отдельно выделяют понятие примитивной пифагоровой тройки. Эта такая тройка, числа которой являются взаимно простыми, то есть не имеют общих делителей. Другими словами, примитивная тройка НЕ может быть получена из другой тройки простым умножением ее чисел на натуральное число. В частности, тройка (3; 4; 5)является примитивной, а «производные» от нее тройки (6; 8; 10) и (9; 12; 15) уже не примитивные.

Интересно, что примитивных троек также бесконечно много. Ещё Евклид предложил алгоритм для их поиска, который, однако, не изучается в рамках школьного курса геометрии.

Задание. Докажите, что у любого прямоугольного треуг-ка с целыми длинами сторон все эти длины не могут быть нечетными числами.

Предположим, что такой треуг-к существует. Пусть его стороны равны a, b и c, и эти числа нечетны. Тогда должно выполняться уравнение:

Заметим, что квадрат нечетного числа также является нечетным числом. Поэтому числа а 2 , b 2 и с 2 – нечетные. Однако сумма нечетных чисел является уже четной. Поэтому выражение а 2 + b 2 четное. Таким образом, получается, что равенство

не может быть верным, ведь его левая часть четна, а правая – нечетна. Поэтому пифагоров треуг-к с тремя нечетными сторонами существовать не может.

Обратная теорема Пифагора

По теореме Пифагора из того факта, что в треуг-ке есть прямой угол, следует следующее соотношение между длинами его сторон:

Оказывается, верно и обратное: если в произвольном треуг-ке одна сторона (очевидно, большая из них) равна сумме квадратов двух других сторон, то из этого следует, что такой треуг-к является прямоугольным.

Это утверждение называют обратной теоремой Пифагора. Докажем её. Пусть есть некоторый ∆АВС, для сторон которого выполняется равенство

Так как ∆А₁В₁С₁ прямоугольный, то для него справедлива теорема Пифагора. Найдем с ее помощью гипотенузу:

а именно это мы и доказываем.

Уточним разницу между собственно теоремой Пифагора и только что доказанной обратной ей теореме. В каждой теореме есть две ключевые части:

1) некоторое условие, которое описывает какое-то геометрическое построение;

2) вывод (или заключение), который делается для условия.

В самой теореме Пифагора в качестве условия описывается прямоугольный треугольник. Для него делается вывод – катеты, возведенные в квадрат, в сумме дадут квадрат гипотенузы.

В обратной же теореме условие и вывод меняются местами. В роли условия описывается треугольник, у которого большая сторона, возведенная во 2-ую степень, равна сумме двух других сторон, также возведенная в квадрат. Для этого описания делается вывод – такой треугольник обязательно должен быть прямоугольным.

Заметим, что не всякая обратная теорема является справедливой. Например, одна из простейших теорем гласит – если углы вертикальные, то они равны. Сформулируем обратную теорему – если углы равны, то они вертикальные. Понятно, что это неверное утверждение.

Задание. Выясните, является ли треуг-к прямоугольным, если его стороны имеют длины:

Решение. Здесь надо просто проверить, являются ли эти числа пифагоровыми тройками. Если являются, то соответствующий треуг-к окажется прямоугольным.

Задание. В ∆КМР проведена биссектриса МН. Её длина 12. КМ = 13 и КН = 5. Найдите МР.

Решение. Рассмотрим ∆МНК. Его стороны равны 5, 12 и 13. Но это одна из пифагоровых троек:

Отсюда следует, что треуг-к прямоугольный, причем МК – гипотенуза (гипотенуза – это длиннейшая сторона). Тогда ∠Н = 90°. Но это означает, что биссектриса МН ещё и высота. Но если в треугольнике одна линия одновременно и медиана, и высота, то это равнобедренный треуг-к, причем КР – его основание. Тогда

Формула Герона

Невозможно построить два треугольника с тремя одинаковыми сторонами. Это значит, что теоретически знания трех сторон треугольника достаточно, чтобы найти его площадь. Но как это сделать? Здесь может помочь формула Герона, которая выводится с помощью теоремы Пифагора.

Пусть стороны треуг-ка равны а, b и с, причем с не меньше, чем а и b. В любом треуг-ке есть хотя бы два острых угла, а тупой угол, если он есть, лежит против большей стороны. Это значит, что оба прилегающих кс угла – острые. Отсюда следует, что высота, опущенная нас, будет лежать внутри треуг-ка. Обозначим длину этой высоты как h. Пусть она разобьет сторону сна два отрезка длиной х и у:

По рисунку можно записать три уравнения:

Левая часть одинакова в обоих уравнениях, значит, равны и правые:

С учетом этого выразим h 2 :

Мы уже выразили высоту (точнее, ее квадрат) через длины сторон. Однако обычно в этой формуле производят замену и вводят число р, равное полупериметру треуг-ка, то есть

Площадь треуг-ка вычисляется по формуле:

Запоминать вывод формулы Герона не надо. Саму формулу всегда можно найти в любом справочнике по геометрии или в Интернете. Достаточно запомнить, что площадь любого треуг-ка можно вычислить, если известны все его стороны.

Задание. Стороны треуг-ка имеют длину 9, 7 и 8 см. Какова его площадь?

Решение. Пусть а = 9; b = 8; с = 7. Для использования формулы Герона сначала вычислим половину периметра треуг-ка:

Итак, сегодня мы узнали о теореме Пифагора. Она представляет собой соотношение, которое связывает катеты и гипотенузу в прямоугольном треуг-ке. Это соотношение помогает в исследованиях других фигур – квадратов, параллелограммов, трапеций. Также с его помощью выведена формула Герона, которая позволяет вычислять площадь треуг-ка, зная только длины его сторон.

Теорема Пифагора и её практическое применение

Управление образования администрации Беловского района

Информационно-методический центр

МОУ «Старопестеревская средняя общеобразовательная школа»

«Теорема Пифагора и её

практическое применение»

I. Историческая справка о Пифагоре…………………………………5

II. Доказательства теоремы Пифагора…………………………………6

III. Использование теоремы Пифагора в решении задач…………..13

IV. Практическое применение теоремы Пифагора

1) архитектура и строительство………………………………..…21

(ок. 580 – ок. 500 г. до н. э.)

Пребудет вечной истина, как скоро

Её познает славный человек!

И ныне теорема Пифагора верна,

Как и в его далёкий век.

Инструментами нашего исследования являются следующие аспекты:

а) объект исследования – т. Пифагора;

б) субъект исследования – геометрическое пространство;

в) предмет исследования – применение т. Пифагора.

Как много лет, и даже столетий, прошло с тех пор, как Пифагор сделал своё открытие. Оно не кануло в Лету – теорему Пифагора люди использовали и в древности, и в средневековье, и продолжают использовать и в наше время.

В данном исследовании мы попытались объединить и систематизировать самые разные стороны применения теоремы Пифагора. Кроме того, мы рассмотрели личность Пифагора, обратили внимание на различные доказательства этой теоремы и решения множества задач по её практическому применению в различных сферах жизни.

Цель: доказать, что «простота, красота и универсальность» теоремы Пифагора позволяет использовать её в различных сферах науки и жизни.

· рассмотреть гипотезы об авторстве доказательства теоремы Пифагора;

· продемонстрировать способы доказательства теоремы Пифагора (например, одно из доказательств «Пифагоровы штаны во все стороны равны»);

· показать применение теоремы Пифагора при решении задач;

· рассмотреть её практическое применение в архитектуре, строительстве, мобильной связи, астрономии.

В своей исследовательской работе использовали монографии по математике, исследовательские разработки, материалы периодической печати, Интернет-ресурсы, мультимедийные компьютерные технологии. В работе представлен объёмный иллюстративный материал в виде таблиц, чертежей, иллюстраций, фотоснимков, рисунков, математических расчётов. Во всех расчетах оперировали приближёнными числовыми значениями величины, так как первоначальные исходные данные получали путём измерений.

Мы представляем результат работы над проектом в виде электронной презентации. Практическое применение нашей работы – использование нашего проекта для элективных курсов, предпрофильной и профильной подготовках и на факультативных занятиях.

Историческая справка о Пифагоре

Пифагор Самосский родился около 580 г. до н. э. на острове Самос в Ионическом море. Пифагор – едва ли не самый популярный учёный за всю историю человечества.

Он принимал в свою школу только тех юношей, которые промолчали в течение пяти лет. Значит, при занятиях математикой нужна абсолютная тишина для того, чтобы можно было сосредоточить все внимание на решении того или другого утверждения.

Пифагор был не только учёным, но и основателем первой научной школы. Он был и воспитателем душ, проповедником собственной «пифагорейской» этики, философом, которого по силе духа и силе воздействия можно сравнить разве с его великими современниками: Конфуцием, Буддой. Но в отличие от них Пифагор создал самую яркую «религию». Он воспитывал в человеке веру в могущество разума, убеждённость в познаваемости природы, уверенность в том, что ключом к тайнам мироздания является математика.

2500 лет тому назад Пифагор направил людей по пути торжества разума. Легенды наперебой объявляют Пифагора чудотворцем. Сообщают, что у него было золотое ребро, что люди видели его одновременно в двух разных городах говорящим со своими учениками, что, однажды, когда он с многочисленными спутниками переходил реку и заговорил с ней, река вышла из берегов и громким голосом воскликнула: «ДА здравствует Пифагор!» Сообщали, что в Тиррении он умертвил своим уксусом ядовитую змею, унёсшую многие жизни. Что он предсказывал землетрясения, отвращал ураганы, укрощал морские волны, останавливал повальные болезни. Порфирий рассказывал о Пифагоре такую историю, что в Торренте он увидел быка, жевавшего новые бобы, подошёл к пастуху и посоветовал сказать быку, чтобы тот этого не делал. Пастух засмеялся и сказал, что он не умеет говорить по-бычьи. Тогда Пифагор сам подошёл к быку и прошептал ему что-то на ухо; после чего бык не только пошёл прочь из бобовника, но и никогда не касался бобов. В 1808 году в Санкт-Петербурге вышла карманного формата книжка «Пифагоровы законы и нравственные правила». Вот некоторые извлечения из этой книги, содержащей 325 заповедей.

Доказательство теоремы Пифагора.

Если дан нам треугольник

И притом с прямым углом,

То квадрат гипотенузы

Мы всегда легко найдём:

Катеты в квадрат возводим,

Сумму степеней находим –

И таким простым путём

К результату мы придём.

Сегодня известно около 500 различных доказательств теоремы Пифагора геометрических, алгебраических, механических и прочих.

Трудно найти человека, который не знал бы её шуточную формулировку: «Пифагоровы штаны во все стороны равны».

А В

Его площадь равна

А В

Площадь большого квадрата равна сумме площадей маленького квадрата и площадей 4-х треугольников

А В

Рассмотрим один из примеров доказательства теоремы Пифагора.

а, в – катеты

с– гипотенуза

Доказать: с2=а2+в2

1) Достроим треугольник до квадрата со

стороной а + в.

Sкв=4∙1/2ав+с2=2ав2+с2

Тогда, 2ав2+с2=(а+в)2

2ав2+с2=а2+2ав+в2

Вычтем из обеих частей 2ав, тогда:

с2=а2+в2,что и требовалось доказать.

1) Прямоугольные треугольники равны по

2) Внутри получается квадрат, т. к. этот

четырёхугольник ромб с прямым углом.

1+2+3=180˚

2+4=90˚ , 3=4, значит 2+3=90˚

Тогда, 1=180˚ – (2+3)=180˚-90˚=90˚

Решение практических задач на применение теоремы Пифагора.

Найти: ВС

ОВ=12 м, ОЕ=5 м, l=50 м

1) Найдём длину одной растяжки. ∆ВОЕ – прямоугольный.

2) Найдём длину 4 растяжек.

Ответ: не хватит.

Дано:АД=10 м, АВ=7 м, СД=4 м

Решение: 1) Провели СК║АД. Тогда АКСД – прямоугольник (объяснить).

Теорема Пифагора

Теорема Пифагора — квадрат гипотенузы равен сумме квадратов катетов (в прямоугольном треугольнике); формула: c² = a² + b².

Доказательство

Доказательство теоремы Пифагора, используя алгебру

Нужно доказать, что c² = a² + b²:

Это квадрат, в котором есть 4 одинаковых треугольника abc:

1. Каждая сторона этого квадрата имеет длину a + b, значит его общая площадь: A = (a + b) (a + b);
2. Площадь наименьшего квадрата (который находится внутри, под наклоном): c²;
3. Площадь каждого из треугольников: ab/2. Значит площадь всех четырёх вместе: 4ab/2 = 2ab;
4. Сумма наименьшего квадрата и треугольников: A = c² + 2ab;
5. Площадь большого квадрата (A = (a + b) (a + b)) равна сумме наименьшего квадрата со всеми треугольниками. Значит:

(a + b) (a + b) = c² + 2ab

a² + 2ab + b² = c² + 2ab

Что и требовалось доказать.

“Пифагоровы штаны на все стороны равны”

Это шуточная фраза, которая именует ещё одно доказательство теоремы Пифагора

На этой фигуре c — гипотенуза, a и b — катеты.

Проведём перпендикулярную линию к гипотенузе (c):

Таким образом появились два новых прямоугольных треугольника (A и B) внутри большого (исходный треугольник С).

1. Общая площадь исходного треугольника (С) равна сумме двух новых, маленьких (A и B): С = А + B;
2. Делим “Пифагоровы штаны” на 3 похожие фигуры:

Все 3 треугольника подобны друг другу (A, B, C) и из-за этого “фигуры-домики” также являются подобными.

Значит соотношение площади A и a² будет одинаковым с площадью B и b², но и с площадью C и c². Т. е.: A/a² = B/b² = C/c² = β (назовём это соотношение греческой буквой бета);

Площадь каждого треугольника, через площадь каждого из квадратов, равна: A = βa², B = βb², C = βc²;

Вспомним, что С = А + B, т. е. βc² = βa² + βb², это равно c² = a² + b².

Что и требовалось доказать.

Примеры

Задача 1

На рисунке видно, что длина одной стороны прямоугольного треугольника составляет 3 см, длина другой — 4 см. Найдите длину гипотенузы.

Подставить известные значения

Ответ: длина гипотенузы равна 5.

Задача 2

Длина одной стороны прямоугольного треугольника составляет 12 см, длина гипотенузы 13 см. Найдите длину другой стороны треугольника.

Подставить известные значения

Ответ: длина другой стороны треугольника равна 5.

Следствия из теоремы Пифагора

Это основные следствия теоремы:

1. В прямоугольном треугольнике гипотенуза всегда больше любого из двух катетов.
2. Если применить формулу теоремы Пифагора (c² = a² + b²) и равенство будет верным, (т.е. если квадрат одной стороны равен сумме квадратов двух других сторон), то треугольник прямоугольный.
3. Из формулы теоремы Пифагора также можно посчитать любой из катетов: a² = c² − b² либо b² = c² − a².
4. Любой косинус (cos) острого угла будет меньше 1.

Кто придумал теорему Пифагора

Концепция теоремы Пифагора была известна ещё в древнем Египте и Вавилоне (около 1900 г. до н. э.). Связь между катетами и гипотенузой в прямоугольном треугольнике была изображена на вавилонской глиняной табличке (которой около 4000 лет). Однако это знание стало широко использоваться лишь после того, как сам Пифагор заявил о нём (он жил в 6 веке до н. э.).

Узнайте также, что такое Теорема Виета и Аксиома.

Теорема Пифагора: история, формулы и доказательства

Теорема Пифагора – одна из самых известных геометрических теорем, которая устанавливает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Большинство ученых считают, что теорема Пифагора была доказана древнегреческим математиком и философом Пифагором (или Питагором). Однако есть версия, что теорему знали и до его рождения. Доказательством этого является то, что в Древнем Египте знали, что треугольник, у которого стороны имеют 3 см, 4 см и 5 см, является прямоугольным. А о других теоремах можно узнать в учебнике по геометрии за 8 класс А.Г. Мерзляка.

Еще в детстве Пифагор отличился интересом к точным наукам. Впоследствии он переехал жить на остров Лесбос, где познакомился с Фалесом Милетским – древнегреческим философом и математиком, который доказал теоремы о трех точках на окружности и пропорциональных отрезках. За время, когда Пифагор учился в Милетской школе, он изучал астрологию, медицину, прогнозы затмений и другие важные в то время науки. Лекции Фалеса и его ученика Анаксимандра сыграли важную роль для Пифагора.

После обучения в Египте, плена в Вавилоне, в 60 лет Пифагор решает вернуться домой, чтобы поделиться своими знаниями с народом. Впоследствии он открыл собственную школу, в которой геометрия впервые выступает как самостоятельная наука.

О том, что квадрат гипотенузы равен сумме квадратов катетов, знали задолго до рождения Пифагора. Но именно он считается первым ученым, который доказал соотношение сторон треугольника.

В теореме Пифагора говорится, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Пусть ВС = а; АС = b; АВ = с.

Тогда имеем такую формулу, которая применяется при нахождении неизвестной стороны в прямоугольном треугольнике, когда две другие – известны:

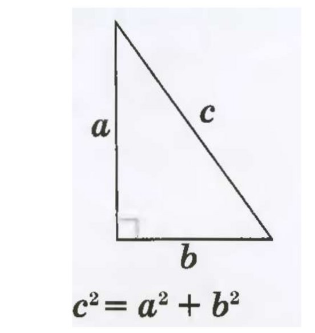
Когда мы определили квадрат гипотенузы, нужно найти квадратный корень. Такую же формулу мы можем применить к неизвестному катету:

А больше рисунков и формул можно увидеть в онлайн уроке за 8 класс по геометрии на тему “Метрические соотношения в прямоугольном треугольнике. Теорема Пифагора”.

Самый популярный и самый простой метод доказательства теоремы связан с площадями фигуры.

Нужно расположить одинаковые прямоугольные треугольники так, чтобы внутри образовался квадрат. Каждая сторона внешнего квадрата должна состоять из суммы катетов прямоугольного треугольника a + b.

Площадь этого квадрата можно будет найти благодаря формуле:

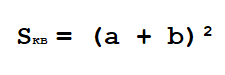
Внутренний четырехугольник можно считать квадратом, ведь, если добавить два острые углы прямоугольного треугольника, то получится 90°. Следует считать, что площадь внешнего квадрата состоит из площади внутреннего квадрата и четырех площадей одинаковых прямоугольных треугольников. Итак, в заключении:

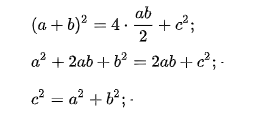
Итак, теорема Пифагора доказана.

2. Доказательство Евклида

Доказательство Евклида также называется “Пифагоровы штаны”. Ее так назвали, потому что сумма площади квадратов, образованных с использованием катетов прямоугольного треугольника равна площади квадрата, который построен на гипотенузе этого же треугольника. Квадраты напоминали ученикам мужские штаны.

На примере приведенных картинок ниже можно увидеть, как оригинально передали суть доказательства Евклида.

В вашем учебнике не было таких доказательств? Вы можете найти другой в разделе “Учебники по геометрии за 8 класс”.

Пример задачи на применение теоремы Пифагора

Условия задачи. В треугольнике ABC дано: ∠C = 90 °, BC = 20 см, AC = 15 см. Найти сторону AB.

Решение. Поскольку в треугольнике АВС ∠С = 90°, следовательно, по теореме Пифагора имеем:

АВ² = BС² + АС²; AВ² = 20² + 15², AВ² = 625, AB = √625| AB = 25 см.

Если вам нужно решить задачу с помощью теоремы Пифагора, а вы сомневаетесь в конечном ответе, тогда можете проверить свои знания благодаря разделу “ГДЗ и решебники по геометрии за 8 класс”.

А если вы хотите крепче закрепить знания по другим темам по геометрии, то можете просматривать видео в разделе “Онлайн уроки за 8 класс по геометрии”. Узнайте больше о перпендикуляре и наклонной, сумме углов выпуклого треугольника, площадь квадрата и прямоугольника, решение задач методом площадей и тому подобное.

Доказательства теоремы Пифагора

• Теорема Пифагора — краткая история
• Формулировка теоремы
• Уравнение
• Доказательство через подобные треугольники
• Другие способы доказательства теоремы
  • Методом площадей
  • Методом бесконечных малых
• Следствие из теоремы Пифагора
• Применение теоремы
  • Расстояние между точками
  • Евклидова метрика
  • Теория чисел
• Примеры решения задач

Этот одна из базовых теорем евклидовой геометрии, определяющая соотношение между сторонами в прямоугольном треугольнике. Несложность доказательства и широкое применение обеспечили ей массовую известность.

Теорема Пифагора — краткая история

Соотношение между сторонами прямоугольного треугольника в том или ином виде было известно многим древним цивилизациям (египетской, шумерской и др.), но первая известная формулировка принадлежит греческому философу и математику Пифагору в V в. до н.э. Об этом известно из труда «Начала», который написал Евклид приблизительно в 300 г. до н. э.

Теорема Пифагора используется для доказательства многих других теорем геометрии. Математиками разработано несколько обобщений, например, для произвольных треугольников, для многомерных пространств. При этом, теорема Пифагора выполняется только в евклидовых геометриях, в иных случаях она не действует.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Формулировка теоремы

Изначальная (геометрическая) формулировка Пифагора гласила:

В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.

Позднее появился алгебраический вариант:

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Оба этих определения эквивалентны. Алгебраическое более элементарно, так как оно не оперирует понятием площади, поэтому теорему в этом виде можно проверить просто – измерив длину гипотенузы и катетов, сделав затем необходимое вычисление.

Уравнение

В виде формулы теорема Пифагора записывается следующим образом:

a 2 +b 2 =c 2 , где:

• а и b – длины двух катетов,
• с – длина гипотенузы.

Доказательство через подобные треугольники

Это доказательство – одно из наиболее простых, так как является прямым следствием аксиом и не оперирует понятием площади.

Имеется прямоугольный треугольник ABC, где C = 90º. Высота, проведенная из прямого угла пересечет гипотенузу в точке H.

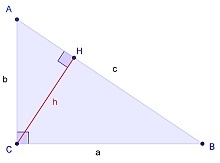
Полученные треугольники ACH и CHB подобны треугольнику АВС по двум углам. Отсюда получаем:

CB 2 =ABxHB, AC 2 =ABxAH

Сложив между собой квадраты катетов, получаем:

AC 2 +CB 2 =ABx(HB+AH)=AB 2

Это и требовалось доказать.

Другие способы доказательства теоремы

Зафиксировано более 400 доказательств теоремы Пифагора. Это связано с простотой ее формулировки, популярностью и широким применением в геометрии. К числу распространенных доказательств относятся методы площадей и бесконечно малых.

Методом площадей

Первоначально требуется дополнительное построение – рисуется квадрат, каждая из сторон которого равна сумме длин катетов a и b. Отложив эти длины, проведем гипотенузы у прямоугольных треугольников:

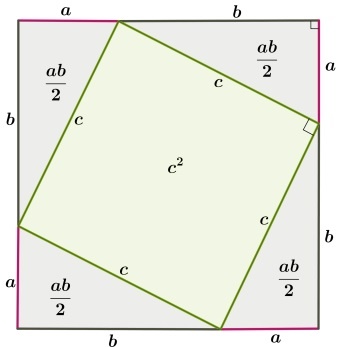
Очевидно, что внутренний четырехугольник, образованный четырьмя гипотенузами, будет квадратом, так как все его стороны равны, а углы прямые. Последнее следует из того, что сумма двух углов треугольника, построенных на гипотенузе равна 90º. Вычитая это значение из развернутого угла в 180º получаем как раз прямой угол.

Площадь внешнего квадрата включает в себя:

• сумму площадей четырех прямоугольных треугольников;
• площадь внутреннего квадрата.

Изменив расположение отрезков на сторонах квадрата и проведя новое построение, можно получить два внутренних квадрата и два прямоугольника. При этом, прямоугольники всегда будут равны, а квадраты будут равными только в частном случае – при равенстве сторон a и b.

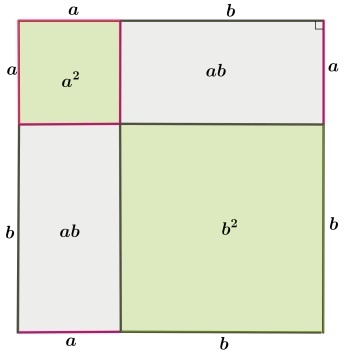
4ab 2 =2ab ⇒ c 2 =a 2 +b 2 , что и нужно было доказать.

Методом бесконечных малых

Данное доказательство делается с помощью интегрального исчисления. Рассматривается ситуация для бесконечно малых приращений сторон треугольника, составляется дифференциальное уравнение и находится его производная.

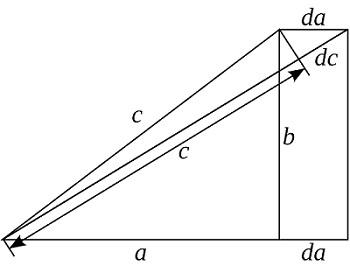
В начале вводится величина d. На это значение увеличивается катет а и гипотенуза с, а катет b остается неизменным. Отсюда имеем

da/ca = c/a, b = const

Разделяя переменные составляется дифференциальное уравнение:

Для его решения необходимо проинтегрировать обе части, при этом получается соотношение:

c 2 = a 2 + const

определяя из начальных условий константу интегрирования, получим:

a = 0 ⇒ c 2 = b 2 = const

Таким образом мы определяем, что

Следствие из теоремы Пифагора

Его так же называют обратной теоремой Пифагора:

Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то такой треугольник прямоугольный.

В алгебраическом виде это можно представить так:

c2=a2+b2, где:

• c – гипотенуза треугольника;
• a и b – его катеты.

Применение теоремы

Благодаря своей универсальности, теорема Пифагора находит себе применение в разных областях математики и других наук. К числу преимуществ ее применения относится прозрачность производимых вычислений.

Расстояние между точками

Одно из главных применений – это определение расстояния между двумя точками в прямоугольной системе координат:

• s – необходимое расстояние;
• (a; b) и (с; d) – координаты двух точек.

Евклидова метрика

В этом случае с помощью теоремы Пифагора находится расстояние в многомерном пространстве:

• n – число измерений данного пространства;
• d (p, q) – необходимое расстояние;
• p(p₁,….,pn) и q(q₁,….,q_n) – две точки, расстояние между которыми нужно найти.

Теория чисел

Арифметическим аналогом теоремы Пифагора стали пифагоровы тройки чисел.

Пифагоровы тройки – группа из трех натуральных чисел x, y и z, удовлетворяющих равенству x2+y2=z2.

Например, к таким числам можно отнести группы (3, 4, 5), (6, 8, 10), (5, 12, 13) и другие. Пифагоровы тройки широко применяются в разных областях деятельности, например, в программировании и криптографии.

Примеры решения задач

Задача 1

В прямоугольном треугольнике АВС, катет ВС = 36 см, гипотенуза АВ = 85 см. Необходимо найти катет АС.

Решение

По теореме Пифагора ВС 2 +АС 2 =АВ 2 , значит

Для нахождения ответа подставим в формулу исходные значения:

Задача 2

Является ли прямоугольным треугольник со сторонами 46, 56 и 76 см.

Решение. Если указанный треугольник прямоугольный, то две меньшие стороны в 46 и 56 см – это катеты, а большая, в 76 см – гипотенуза. По теореме Пифагора сумма квадратов катетов должна быть равна квадрату гипотенузы. Проверим это:

• 46²+56²= 5252;
• 76²= 5776;
• 5252 ≠ 5776, значит, указанный треугольник не является прямоугольным.

Задача 3.

Диагонали ромба ABCD равны 24 и 18 см. Чему равна сторона ромба.

Решение

Диагонали ромба AC и BD пересекаются под прямым углом и точкой пересечения O делятся пополам. В этом виде задача сводится к поиску гипотенузы АВ в прямоугольном треугольнике ABO с катетами АО=24/2=12 см и ВО=18/2=9 см.