Как найти объем цилиндра: формула через диаметр и высоту
Объем цилиндра

Объем цилиндра равен произведению площади его основания на высоту.
Формулы объема цилиндра:
Объем цилиндра формула (через радиус основания и высоту)
r — радиус основания цилиндра,
h — высота цилиндра
Если внимательно посмотреть на эту формулу, то можно заметить, что
Зная радиус r и высоту h
Чему равен объем цилиндра V если известны его радиус r и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:
V = 3.14156 ⋅ 2 2 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см 3
Зная диаметр d и высоту h
Чему равен объем цилиндра V если известны его диаметр d и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:
V = 3.14156 ⋅ ( 1 /2) 2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см 3
Формула вычисления объема цилиндра
1. Через площадь основания и высоту
Объем (V) цилиндра равняется произведению его высоты и площади основания.
V = S ⋅ H

2. Через радиус основания и высоту
Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R 2 . Следовательно, формулу для вычисления объема цилиндра можно представить в виде:
V = π ⋅ R 2 ⋅ H
Примечание: в расчетах значение числа π округляется до 3,14.
3. Через диаметр основания и высоту
Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:
V = π ⋅ (d/2) 2 ⋅ H
Введите радиус основания и высоту цилиндра

Цилиндр – геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула объема цилиндра:
 , где R – радиус оснований, h – высота цилиндра
, где R – радиус оснований, h – высота цилиндра
Примеры задач
Задание 1
Найдите объем цилиндра, если дана площадь его основания – 78,5 см 2 , а также, высота – 10 см.
Решение:
Применим первую формулу, подставив в нее известные значения:
V = 78,5 см 2 ⋅ 10 см = 785 см 3 .
Задание 2
Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.
Решение:
Воспользовавшись третьей формулой, в которой участвует диаметр, получаем:
V = 3,14 ⋅ (8/2 см) 2 ⋅ 6 см = 301,44 см 3 .
Поэтапный расчет объема картонной коробки
Для расчета нужно:
-
Измерить длину а и ширину b, если дно коробки квадратное, то а=b; Измерить высоту h как расстояние от нижнего до верхнего клапана коробки.
Сначала нужно рассчитать внутренний объем коробки, необходимый для размещения груза. Габаритные размеры груза должны быть на 5–10 мм меньше, чем внутренние размеры гофроупаковки.
V=a*b*h
где a – длина основания (м), b – ширина основания (м),
h – высота коробки (м).
V=S*h
где S — площадь основания коробки, а h — ее высота.
Объем, занимаемый заготовкой (коробкой) (с учетом толщины стенок) рассчитывается для правильного размещения внутри транспортного средства или хранения на складе.
Формула для расчета занимаемого объема:
V=Площадь (S) * толщину листа
*как рассчитать площадь (S) картонной коробки — в этой статье
| Тип: | Профиль: | Толщина (мм): |
| Трехслойный гофрокартон | B | 3 |
| Трехслойный гофрокартон | C | 3,7 |
| Трехслойный гофрокартон | E | 1,6 |
| Пятислойный гофрокартон | BC | 7 |
| Пятислойный гофрокартон | BE | 4 |
 Перемножив полученные значения, получим объем коробки в кубических метрах. Чтобы получить результат в литрах необходимо полученное значение в м 3 умножить на 1000.
Перемножив полученные значения, получим объем коробки в кубических метрах. Чтобы получить результат в литрах необходимо полученное значение в м 3 умножить на 1000.
Подсчет объема коробки в литрах
При транспортировке мелких или сыпучих товаров их также пакуют в ящики. Учитывая, что такие предметы и материалы занимают весь объем тары, нужно знать их количество в литрах. Если Вы интересуетесь, как посчитать объем короба в литрах, определяйте литраж следующим образом:
находим кубатуру V=a*b*h =0,3*0,25*0,15=0,0112 м 3 ;
зная равенство: 1 м 3 = 1000 л, переводим полученное значение в литры: V=0,0112 *1000=1,2 л.
Объем цилиндрической полости
Объем полости в виде цилиндра равен объему цилиндра, который извлечен из данной полости для ее образования. То есть для вычисления цилиндрической полости можно воспользоваться формулами и калькулятором для расчета простого правильного цилиндра в зависимости от известных исходных данных.
На картинке продемонстрирована цилиндрическая полость, образованная в теле путем извлечения из него цилиндра. Объем извлеченного цилиндра и объем образованной полости равны.
Нужно отметить один важный момент. Несмотря на равенство объемов извлеченного цилиндра и образованной полости, площади поверхностей данных объектов будут отличаться, так как у образованной цилиндрической полости отсутствует верхняя поверхность. То есть суммарная площадь поверхности образованной цилиндрической полости будет меньше суммарной площади извлеченного цилиндра на одну площадь основания цилиндра.
Цилиндр может быть правильным или наклонным 
Правильный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра равен 90 градусов.
Неправильный или наклонный цилиндр – это цилиндр, где угол между образующими боковой поверхности и основанием цилиндра отличается от 90 градусов.
Рассмотрим правильный цилиндр.
Цилиндр – это тело, образованное вращением прямоугольника вокруг одной из его сторон. Тело цилиндра ограничено двумя кругами, называемыми основанием цилиндра и боковой цилиндрической поверхностью, которая в развертке представляет собой прямоугольник
Цилиндр можно так же описать как тело, состоящее из двух равных кругов, не лежащих в одной плоскости и параллельных между собой, и отрезков, соединяющих все точки одной окружности, с соответствующими точками другой окружности. Данные отрезки называются образующими цилиндра.
Радиус основания цилиндра, является радиусом цилиндра.
Ось цилиндра – это прямая, соединяющая центра оснований цилиндра.
Высота цилиндра – это перпендикуляр, опущенный от одного основания цилиндра к другому.
Объем прямого цилиндра
Цилиндр – это геометрическое тело, которое сформировано вращением прямоугольника на оси, совпадающей с одним из его сторон. Слово «цилиндр» происходит от греческого слова «kylindros».
Объем цилиндра через площадь основания и высоту цилиндра
Объем цилиндра равен произведению площади основания цилиндра на его высоту.
[ LARGE V = S cdot H ]
где:
V – объем цилиндра
H – высота цилиндра
S – площадь цилиндра
Поверхности цилиндра
Наружную поверхность цилиндра можно условно разделить на три отдельные поверхности: верхняя, нижняя и боковая.
Верхняя и нижняя поверхности цилиндра имеют форму круга и равны между собой.
Боковая поверхность цилиндра имеет форму прямоугольника. Чтобы это наглядно представить, возьмем боковую наружную поверхность цилиндра и мысленно сделаем вертикальный разрез по образующей цилиндра. Далее развернем поверхность на плоскость. В результате увидим, что боковая поверхность имеет форму прямоугольника (см. на картинке).
Сечения цилиндра

При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом в 90 градусов, всегда получатся прямоугольная фигура 
При сечении цилиндра плоскостью, проходящей через оба основания цилиндра под углом отличным от 90 градусов, получатся фигура, похожая на прямоугольник  , но две боковые стороны которого будут являться кривыми линиями.
, но две боковые стороны которого будут являться кривыми линиями.
Если секущая поверхность проходит параллельно основаниям цилиндра, то сечением будет круг 
Если секущая поверхность проходит через боковую поверхность, но при этом не параллельна основанию цилиндра, то в сечении получается эллипс 
Если секущая поверхность проходит через одно основание цилиндра и боковую поверхность, то в сечение будет фигура в виде половины эллипса 
Как рассчитать объем цилиндра с помощью калькулятора
Калькулятор позволяет определить объем цилиндра по одному из 3 вариантов:
- площадь основания и высота цилиндра;
- радиус основания и высота цилиндра;
- диаметр основания и высота цилиндра.
Выберите соответствующий шаг и введите исходные данные в соответствующие поля.
Также важно указать единицы измерения по условиям задачи.
Расчеты будут выполнены автоматически и конвертированы в основные метрические физические величины объема.
Онлайн калькулятор. Объем цилиндра.
Как рассчитать объем цилиндра в м3, литрах и куб.см? Наш калькулятор сделает все расчёты моментально сразу во всех единицах.
- Объемы фигур
- Онлайн-калькулятор объема цилиндра
- Объем правильного цилиндра через радиус и высоту цилиндра
- Онлайн калькулятор
- Зная радиус r и высоту h
- Формула
- Пример
- Зная диаметр d и высоту h
- Формула
- Пример
- Зная площадь основания So и высоту h
- Формула
- Пример
- Зная площадь боковой поверхности Sb и высоту h
- Формула
- Пример
- Как вычислить объём цилиндра
- Объем цилиндра по высоте и радиусу
- Вычислить, найти объем цилиндра по формуле (1).
- Объем цилиндра
- Скачать, сохранить результат
- Выберите способ сохранения
- Калькуляторы по геометрии
- Формула объема кругового цилиндра
Объемы фигур
Онлайн-калькулятор объема цилиндра
Это определение самого простого, так называемого, прямого кругового цилиндра. Более полное и общее определение цилиндра следующее:
Цилиндром называют геометрическое тело, которое получается путем пересечения двух плоскостей, которые параллельны друг другу, с прямыми, которые так же параллельны друг другу.
Эти прямые получили название образующих цилиндра. Плоскости – это основания цилиндра.
Прямая, которая перпендикулярна плоскостям, содержащим основания цилиндра, называется высотой данного цилиндра.
Объем правильного цилиндра через радиус и высоту цилиндра
– Вычисления (показано) (скрыто)
– примечания (показано) (скрыто)
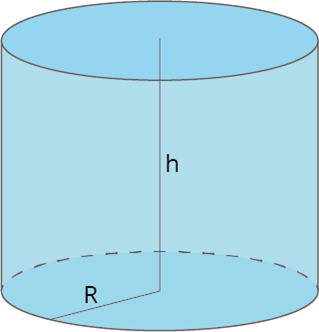
r – радиус основания цилиндра
h – высота цилиндра
Площадь основания цилиндра
Площадь боковой поверхности
Онлайн калькулятор

Найти чему равен объем цилиндра (V) можно зная (либо-либо):
- радиус r и высоту h цилиндра
- диаметр d и высоту h цилиндра
- площадь основания So и высоту h цилиндра
- площадь боковой поверхности Sb и высоту h цилиндра
Подставьте значения в соответствующие поля и получите результат.
Зная радиус r и высоту h
Чему равен объем цилиндра если его радиус
Чему равен объем цилиндра V если известны его радиус r и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 8 см, а его радиус r = 2 см, то:
V = 3.14156 ⋅ 22 ⋅ 8 = 3.14156 ⋅ 32 = 100.53 см3
Зная диаметр d и высоту h
Чему равен объем цилиндра если его диаметр
Чему равен объем цилиндра V если известны его диаметр d и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 5 см, а его диаметр d = 1 см, то:
V = 3.14156 ⋅ (1/2)2 ⋅ 5 = 3.14156 ⋅ 1.25 ≈ 3.927 см3
Зная площадь основания So и высоту h
Чему равен объем цилиндра если площадь его основания
Чему равен объем цилиндра V если известны его площадь основания So и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 10 см, а площадь его основания So = 5 см2, то:
V = 10 ⋅ 5 = 50 см3
Зная площадь боковой поверхности Sb и высоту h
Чему равен объем цилиндра если площадь его боковой поверхности
Чему равен объем цилиндра V если известны его площадь боковой поверхности Sb и высота h?
Формула
Пример
Если цилиндр имеет высоту h = 5 см, а площадь его боковой поверхности Sb = 30 см2, то:
V = 302/ 4 ⋅ 3.14⋅ 5 = 900/62.8 = 14.33 см3
Как вычислить объём цилиндра
- Сначала необходимо выбрать через какие исходные величины будут производиться вычисления. Для того чтобы найти объём цилиндра нужно знать его высоту, а также радиус, диаметр или площадь основания. Для каждого способа используется своя формула.
- Далее требуется ввести начальные значения и единицы измерения исходных величин.
- Результат будет округлён до указанного знака после запятой.
- Объём цилиндра можно выразить в мм3, см3, дм3, м3 и литрах.
- Кнопка “рассчитать” производит вычисление согласно заданному условию.
Объем цилиндра по высоте и радиусу

Узнать объем полой фигуры можно моментально, воспользовавшись удобной онлайн-программой. Сервис позволяет за секунды вычислить параметры тела и получить результаты в кубических сантиметрах, метрах, литрах. Расчет производится по двум математическим формулам:
- По высоте и радиусу: V = S х h.
Где V – объем, S – площадь, h – высота. Чтобы рассчитать объем необходимо площадь основания тела умножить на h. Следовательно, для этого необходимо знать две переменные.
Объём по площади основания и высоте: V = ∏ х R2 х h
R – радиус, возведенный в квадрат. От первой формулы, расчет отличается тем, что сначала необходимо найти значение радиуса. Для этого диаметр делится на 2 или применяется формула S/2 х ∏ х H. ∏ – константа 3,14 (отношение длины окружности к диаметру).
Вычислить, найти объем цилиндра по формуле (1).
| R (радиус вращения) |
| H (высота цилиндра) |
нажмите кнопку для расчета
Объем цилиндра
Скачать, сохранить результат
Выберите способ сохранения
Вы можете сохранить результат расчёта в формате PDF на ваше устройство.
Распечатайте результат расчёта конструкции на бумагу любого формата.
Отправьте результат расчета в формате PDF на ваш е-мейл.
Калькуляторы по геометрии
Формула объема кругового цилиндра
Для того, чтобы вычислить объем прямого кругового цилиндра нужно просто умножить площадь его основания (то есть, площадь круга, лежащего в основании цилиндра) на высоту этого цилиндра.
Формула объема кругового цилиндра
V=Sосн⋅hV=S_
SоснS_
hh h — высота этого цилиндра.
Для кругового цилиндра, площадь основания SоснS_
Sосн=π⋅R2S_
RR R — радиус круга.
Рассмотрим несколько примеров.
Найдите объем цилиндра, если площадь его основания равна 196π см2196pitext< см>^2 1 9 6 π см 2 , а его высота hh h в 2 раза больше радиуса основания RR R .
Решение
Sосн=196πS_
h=2⋅Rh=2cdot R h = 2 ⋅ R
Сначала вычисляем радиус основания:
Sосн=π⋅R2S_
Выразим отсюда радиус RR R :
R2=SоснπR^2=frac
R=196ππR=sqrt
R=196R=sqrt <196>R = 1 9 6
По условию задачи, высота цилиндра в два раза больше RR R :
h=2⋅R=2⋅14=28h=2cdot R=2cdot 14=28 h = 2 ⋅ R = 2 ⋅ 1 4 = 2 8
Тогда объем цилиндра по формуле:
V=Sосн⋅h=196⋅π⋅28≈17232 см3V=S_
Ответ
17232 см3.17232text< см>^3. 1 7 2 3 2 см 3 .
Определить, чему равен объем цилиндра, если радиус его основания RR R равен 7 см7text < см>7 см , а высота – 14 см14text < см>1 4 см .
Решение
R=7R=7 R = 7
h=14h=14 h = 1 4
По формуле для объема цилиндра получаем:
V=Sосн⋅h=π⋅R2⋅h=π⋅72⋅14≈2154 см3V=S_
Ответ
2154 см3.2154text< см>^3. 2 1 5 4 см 3 .
В квадрат со стороной aa a равной 4 см4text < см>4 см вписана окружность, являющаяся основанием цилиндра, высота которого равна 20 см20text < см>2 0 см . Вычислите его объем.
Решение
a=4a=4 a = 4
h=20h=20 h = 2 0
Исходя из того, что сторона квадрата, в который вписана окружность, равна диаметру DD D этой окружности, можно найти площадь основания цилиндра:
Sосн=π⋅R2=π⋅D24=π⋅a24=π⋅424≈12.56S_
V=Sосн⋅h≈12.56⋅20=251.2 см3V=S_
Ответ
251.2 см3.251.2text< см>^3. 2 5 1 . 2 см 3 .
Уравнения с параметрами.
Исследование и решение уравнений с параметрами считается не самым простым разделом школьной математики. Однако, параметр, как понятие, часто воспринимается школьниками гораздо более сложным, чем есть в действительности. Здесь в первом пункте представлены очень простые вводные примеры использования параметров в уравнениях. Те, для кого это понятие не составляет большой трудности, могут сразу перейти к решению задач, которые представлены ниже.
Что такое уравнение с параметром?
Допустим нам нужно решить уравнение 2х + 5 = 2 − x.
Решение: 2x + x = 2 − 5; 3x = −3; x = −3/3 = −1.
Теперь нужно решить уравнение 2x + 5 = 3 − x.
Решение: 2x + x = 3 − 5; 3x = −2; x = −2/3
Затем нужно решить уравнение 2x + 5 = 0,5 − x.
Решение: 2x + x = 0,5 − 5; 3x = −4,5; x = −4,5/3 = −1,5.
А потом может потребоваться решить уравнение 2x + 5 = 10,7 − x или уравнение 2x + 5 = −0,19 − x.
Понятно, что уравнения похожи, а потому их решение будет сопровождаться теми же действиями, что выше. Возникает естественный вопрос – сколько можно делать одно и то же?
Уменьшим себе трудозатраты. Заметим, что все эти уравнения отличаются только одним числом в правой части. Обозначим это число символом a .
Получим уравнение 2х + 5 = a − х,
где a – переменная величина, вместо которой можно подставить нужное числовое значение и получить нужное уравнение. Эта переменная и называется параметром.
Решим это уравнение так же, как и все предыдущие.
Решение: 2х + 5 = a − x; 2x + x = a − 5; 3x = a − 5; x = (a − 5)/3.
Теперь для того, чтобы найти ответы для двух последних примеров, мы можем не повторять полностью всё решение каждого уравнения, а просто подставить в полученную формулу для х числовое значение параметра а:
x = (10,7 − 5)/3 = 5,7/3 = 1,9;
x = (−0,19 − 5)/3 = −5,19/3 = −1,73.
Таким образом, под термином “уравнение с параметром”, фактически, скрывается целое семейство “почти одинаковых уравнений” , которые отличаются друг от друга только одним числом (одним слагаемым или одним коэффициентом) и одинаково решаются. Параметр – это число, которое меняется от уравнения к уравнению.
Полученную формулу для корня уравнения мы можем запрограммировать на компьютере. Достаточно будет только ввести значение параметра a, чтобы получить решение любого такого уравнения.
Рассмотрим еще один пример.
Замечаем, что они похожи друг на друга и отличаются только первым коэффициентом. Обозначим его, например, символом k.
Решим уравнение kх + 5 = 2 − x с параметром k.
С помощью этой формулы вычислим все ответы для приведенных уравнений.
x = −3/(2 + 1) = −1
x = −3/(3 + 1) = −0,75
x = −3/(−4 + 1) = 1
x = −3/(17 + 1) = −1/6
Можем ли мы теперь запрограммировать эту формулу и сказать, что с её помощью можно решить любое аналогичное уравнение?
Запрограммировать можем. Компьютер справится как с очень большими значениями коэффициента, так и с очень маленькими.
Например, если введём k = 945739721, то для уравнения заданного вида будет получен корень примерно равный −0,0000000031721201195353831188, если k = 0,0000004, то получим корень ≈ −2,9999988000004799998080000768.
Но, если мы введем в программу, казалось бы, более простое значение k = −1, то компьютер зависнет.
Почему?
Посмотрим внимательнее на формулу x = −3/(−1 + 1) = −3/0. Деление на ноль.
Посмотрим на соответствующее уравнение −1·х + 5 = 2 − x.
Преобразуем его −х + x = 2 − 5.
Оказывается, оно равносильно уравнению 0 = −3 (. ) и не может иметь корней.
Таким образом, из общего подхода к решению “почти одинаковых уравнений” могут существовать исключения, о которых нужно позаботиться отдельно. Т.е. провести предварительное исследование всего семейства уравнений. Именно этому и учатся на уроках математики с помощью так называемых задач с параметрами.
Графические способы решения уравнений
Сначала вспомним, что представляет собой графический способ решения обычного уравнения (без параметра).
Пусть дано уравнение вида f(x) = g(x) . Построим графики функций y = f(x) и y = g(x) и найдём точки пересечения этих графиков. Абсциссы точек пересечения и есть корни уравнения.
Для быстрого построения эскизов графиков повторите еще раз графики элементарных функций, которые изучаются в школьном курсе математики, и правила преобразования графиков функций.
Рассмотрим примеры.
1. Решить уравнение
2х + 5 = 2 − x

Ответ: x = −1.
2. Решить уравнение
2х 2 + 4х − 1 = 2х + 3

3. Решить уравнение
log2х = −0,5х + 4

Ответ: x = 2.
Первые два из приведенных уравнений вы можете решить и аналитически, так как это обычные линейное и квадратное уравнения. Второе уравнение содержит функции разных классов – степенную (здесь линейную) и трансцендентную (здесь логарифмическую). Для таких случаев выбор способов решения у школьников очень ограничен. Фактически, единственным доступным способом является именно графическое решение.
Внимание: Для корней, найденных графическим способом, обязательна проверка! Вы уверены, что на третьем рисунке пересечение именно в точке х = 4 , а не в точке 3,9 или 4,1? А если на реальном экзамене у вас нет возможности построить график достаточно точно? На чертеже “от руки” разброс может быть еще больше. Поэтому алгоритм действий должен быть следующим:
- Предварительный вывод: х ≈ 4.
- Проверка: log24 = −0,5·4 + 4; 2 = −2 + 4; 2 ≡ 2.
- Окончательный вывод х = 4.
Чтобы графически решать уравнения с параметрами надо строить не отдельные графики, а их семейства.
Решение уравнений с параметрами с помощью графиков.
Задача 1.
Найти все значения параметра q при которых уравнение |x + 1| − |x − 3| − x = q 2 − 8q + 13 имеет ровно 2 корня.
При каждом значении параметра q можно вычислить значение выражения q 2 − 8q + 13 . Результат обозначим переменной а.
Т.е. примем q 2 − 8q + 13 = a и решим уравнение с параметром |x + 1| − |x − 3| − x = a
Строим график функции y = |x + 1| − |x − 3| − x , расположенной в левой части уравнения.
Для этого разобьём числовую ось на отрезки точками, в которых каждый из встречающихся модулей принимает нулевое значение.

Для каждого из этих участков раскроем модули с учётом знаков.
Вспомним: по определению |x| = x, если х ≥ 0, и |x| = −x, если х Чтобы проверить знаки модулей на участке достаточно подставить любое промежуточное значение x из этого отрезка, например, −2, 0 и 4.
Таким образом на участке I, где −∞ имеем −(x + 1) + (x − 3) − x = − x − 4.
Следовательно, должны построить график функции y = − x − 4 .
Это линейная функция. Её график прямая линия, которую можно построить по двум точкам, например, x = 0, y = −4 и у = 0, x = −4. Cтроим всю прямую бледной линией, а затем выделяем часть графика, относящуюся только к рассматриваемому участку.
Аналогично, разбираемся с оставшимися двумя участками.
На участке II, где −1 имеем (x + 1) + (x − 3) − x = x − 2
и должны построить соответствующую часть графика функции y = x − 2 .
На участке III, где 3 , имеем (x + 1) − (x − 3) − x = − x + 4
и должны построить соответствующую часть графика функции y = − x + 4 .
Последовательное построение итогового графика показано ниже. (Чтобы увеличить рисунок, нужно щелкнуть по нему левой кнопкой мыши.)






Замечание: если вы освоили тему Преобразование графиков функций, то с этой частью задачи сможете справиться быстрее, чем показано в примере.
Итак, построение графика функции, расположенной в левой части уравнения, мы завершили. Посмотрим, что находится в правой части.
График функции y = a представляет собой прямую линию, параллельную оси абсцисс (Ox), и пересекающую ось ординат (Oy) в точке а. Так как а – параметр, который может принимать разные значения, то нужно построить целое семейство таких параллельных линий, пересекающих ось ординат на разной высоте. Очевидно, что все графики семейства построить мы не сможем, поскольку их бесконечное множество. Изобразим для примера несколько штук в районе уже построенного графика функции. Ниже прямые семейства y = a показаны красным цветом.


Из рисунка видно, что количество точек пересечения каждой из красных прямых с ранее построенным (зелёным) графиком зависит от высоты, на которой расположена эта прямая, т.е. от параметра а. Прямые, расположенные ниже y = −3 , пересекают график в одной точке, а значит эти уравнения имеют только одно решение. Прямые, проходящие на уровне −3 имеют по три точки пересечения, значит соответствующие уравнения будут иметь по три решения. Прямые, расположенные выше точки y = 1 , снова имеют только по одной точке пересечения.
Ровно две точки пересечения с зелёным графиком будут иметь только прямые y = 1 и y = −3 . Соответствующие уравнения будут иметь ровно два корня, что и требовалось определить в задании.
Однако мы нашли значения введённого нами параметра а, при котором заданное уравнение имеет 2 корня, а вопрос задачи состоял в том, чтобы найти все значения параметра q. Для этого придётся решить следующую совокупность уравнений: 
Это обычные квадратные уравнения, которые решаются через дискриминант или по теореме Виета. 
Таким образом, окончательный ответ: <2;4;6>.
Задача 2.
Найти все значения параметра a, при которых уравнение (2 − x)x(x − 4) = a имеет ровно 3 корня.
Рассмотрим функцию y = (2 − x)x(x − 4) . Видно, что если раскрыть скобки, то старший член будет −х 3 . Т.е. графиком функции должна быть кубическая парабола, причем на при x, стремящемcя к +∞, y → −∞, а при x, стремящемся к −∞, y → +∞.
Поскольку уравнение (2 − x)x(x − 4) = 0 имеет три корня 2, 0 и 4, то график функции будет пересекать ось абсцисс трижды.
Понятно, что при упомянутых условиях график непрерывной функции должен иметь участок с “волной”. Строим от руки эскиз графика.
Правая часть уравнения y = a такая же, как в предыдущей задаче. Поэтому дальнейшие построения не требуют комментариев. Смотрите рисунки. Чтобы увеличить, используйте щелчок мышью.






Из рисунков видно, что прямые, отделяющие линии с тремя точками пересечения от других случаев, проходят через экстремумы кубической функции. Поэтому определяем значения ymax и ymin через производную. (Исследовать функцию полностью не нужно, так как примерное положение точек экстремума мы видим на эскизе графика.) Обратите внимание на то, что при вычислении значений функции используются точные значения x и формулы сокращенного умножения. Приближенные значения в промежуточных вычислениях не используют.
Ответ: 
Задача для самостоятельного решения
Задача 3.
При каком наибольшем отрицательном значении параметра а уравнение  имеет один корень?
имеет один корень?
Ответ: -1,625
Задача реального экзамена ЗНО-2013 (http://www.osvita.ua/).
Переход на главную страницу сайта “Математичка”.

Есть вопросы? пожелания? замечания?
Обращайтесь – mathematichka@yandex.ru
Внимание, ©mathematichka. Прямое копирование материалов на других сайтах запрещено. Ставьте гиперссылку.
Уравнения с параметром
Разделы: Математика
Справочный материал
Уравнение вида f(x; a) = 0 называется уравнением с переменной х и параметром а.
Решить уравнение с параметром а – это значит, для каждого значения а найти значения х, удовлетворяющие этому уравнению.
Если 1 – а = 0, т.е. а = 1, то х0 = -2 корней нет
Если 1 – а  0, т.е. а
0, т.е. а  1, то х =
1, то х = 
Пример 4.
(а 2 – 1) х = 2а 2 + а – 3
(а – 1)(а + 1)х = 2(а – 1)(а – 1,5)
(а – 1)(а + 1)х = (1а – 3)(а – 1)
Если а = 1, то 0х = 0
х – любое действительное число
Если а = -1, то 0х = -2
Корней нет
Если а  1, а
1, а  -1, то х =
-1, то х =  (единственное решение).
(единственное решение).
Это значит, что каждому допустимому значению а соответствует единственное значение х.
если а = 5, то х =
=
;
если а = 0, то х = 3 и т. д.
Дидактический материал
2. 4 + ах = 3х – 1
3. а =  +
+ 
4.  + 3(х+1)
+ 3(х+1)
5.  =
=  –
– 
6.  =
= 
Ответы:
- При а
 1 х =
1 х = ;
;
- При а
 3 х =
3 х =  ;
;
- При а
 1, а
1, а -1, а
-1, а 0 х =
0 х =  ;
;
при а = 1 х – любое действительное число, кроме х = 1
при а = -1, а = 0 решений нет.
- При а
 2, а
2, а 0 х =
0 х =  ;
;
при а = 0, а = 2 решений нет.
- При а
 -3, а
-3, а -2, а
-2, а 0, 5 х =
0, 5 х = 
при а = -3, а = 0, 5, а = -2 решений нет
- При а + с
 0, с
0, с 0 х =
0 х =  ;
;
при а = –с, с = 0 решений нет.
Квадратные уравнения с параметром
Пример 1. Решить уравнение
При а = 1 6х + 7 = 0
х = – 
В случае а  1 выделим те значения параметра, при которых Д обращается в нуль.
1 выделим те значения параметра, при которых Д обращается в нуль.
Д = (2(2а + 1)) 2 – 4(а – 1)(4а + 30 = 16а 2 + 16а + 4 – 4(4а 2 + 3а – 4а – 3) = 16а 2 + 16а + 4 – 16а 2 + 4а + 12 = 20а + 16
20а + 16 = 0
a = 
a = 
Если а -4/5 и а  1, то Д > 0,
1, то Д > 0,
х = 
Если а = 4/5, то Д = 0,
х = –  = –
= – 
Пример 2. При каких значениях параметра а уравнение
х 2 + 2(а + 1)х + 9а – 5 = 0 имеет 2 различных отрицательных корня?
Д = 4(а + 1) 2 – 4(9а – 5) = 4а 2 – 28а + 24 = 4(а – 1)(а – 6)
4(а – 1)(а – 6) > 0
по т. Виета: х1 + х2 = -2(а + 1)
х1х2 = 9а – 5
По условию х1 0
Пример 3. Найдите значения а, при которых данное уравнение имеет решение.
х 2 – 2(а – 1)х + 2а + 1 = 0
Д = 4(а – 1) 2 – 4(2а + 10 = 4а 2 – 8а + 4 – 8а – 4 = 4а 2 – 16а
4а 2 – 16 
4а(а – 4) 
а(а – 4)) 
а(а – 4) = 0
а = 0 или а – 4 = 0
а = 4
Ответ: а  0 и а
0 и а  4
4
Дидактический материал
1. При каком значении а уравнение ах 2 – (а + 1) х + 2а – 1 = 0 имеет один корень?
2. При каком значении а уравнение (а + 2) х 2 + 2(а + 2)х + 2 = 0 имеет один корень?
3. При каких значениях а уравнение (а 2 – 6а +  х 2 + (а 2 – 4) х + (10 – 3а – а 2 ) = 0 имеет более двух корней?
х 2 + (а 2 – 4) х + (10 – 3а – а 2 ) = 0 имеет более двух корней?
4. При каких значениях а уравнение 2х 2 + х – а = 0 имеет хотя бы один общий корень с уравнением 2х 2 – 7х + 6 = 0?
5. При каких значениях а уравнения х 2 +ах + 1 = 0 и х 2 + х + а = 0 имеют хотя бы один общий корень?
1. При а = – 1/7, а = 0, а = 1
2. При а = 0
3. При а = 2
4. При а = 10
Показательные уравнения с параметром
Пример 1.Найти все значения а, при которых уравнение
9 х – (а + 2)*3 х-1/х +2а*3 -2/х = 0 (1) имеет ровно два корня.
Решение. Умножив обе части уравнения (1) на 3 2/х , получим равносильное уравнение
3 2(х+1/х) – (а + 2)*3 х+1/х + 2а = 0 (2)
Пусть 3 х+1/х = у, тогда уравнение (2) примет вид у 2 – (а + 2)у + 2а = 0, или
(у – 2)(у – а) = 0, откуда у1 =2, у2 = а.
Если у = 2, т.е. 3 х+1/х = 2 то х + 1/х = log32 , или х 2 – хlog32 + 1 = 0.
Это уравнение не имеет действительных корней, так как его Д = log 2 32 – 4 х+1/х = а то х + 1/х = log3а, или х 2 – хlog3а + 1 = 0. (3)
Уравнение (3) имеет ровно два корня тогда и только тогда, когда
Д = log 2 32 – 4 > 0, или |log3а| > 2.
Если log3а > 2, то а > 9, а если log3а 9.
Пример 2. При каких значениях а уравнение 2 2х – (а – 3) 2 х – 3а = 0 имеет решения?
Для того чтобы заданное уравнение имело решения, необходимо и достаточно, чтобы уравнение t 2 – (a – 3) t – 3a = 0 имело хотя бы один положительный корень. Найдем корни по теореме Виета: х1 = -3, х2 = а = >
а – положительное число.
Ответ: при а > 0
Дидактический материал
1. Найти все значения а, при которых уравнение
25 х – (2а + 5)*5 х-1/х + 10а * 5 -2/х = 0 имеет ровно 2 решения.
2. При каких значениях а уравнение
2 (а-1)х?+2(а+3)х+а = 1/4 имеет единственный корень?
3. При каких значениях параметра а уравнение
4 х – (5а-3)2 х +4а 2 – 3а = 0 имеет единственное решение?
Ответ:
- 0 25/2
- при а = 1, а = -2,2
- 0 0, х
 1/4 (3)
1/4 (3)
 х = у
х = у
ау 2 –у + 1 = 0 (4)
| Если а = 0, то – | 2у + 1 = 0 2у = 1 у = 1/2  х = 1/2 х = 1/2 х = 1/4 |
Не выполняется (2) условие из (3).
Пусть а  0, то ау 2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а
0, то ау 2 – 2у + 1 = 0 имеет действительные корни тогда и только тогда, когда Д = 4 – 4а  0, т.е. при а
0, т.е. при а  1.
1.
Если Д = 0 (а = 1), то (4) имеет единственный положительный корень х = 1, удовлетворяющий условиям (3).
Пусть Д > 0 (а 0 уравнение (4) имеет действительные корни разных знаков. Это условие выполняется тогда и только тогда, когда Д > 0 и 1/а х
Выражая х из (1) и подставляя в (2), получаем неравенство
 2 – а > 1 – а (3)
2 – а > 1 – а (3)
Чтобы решить неравенство (3), построим графики функций у =  2 – а и у = 1 – а.
2 – а и у = 1 – а.
Решения неравенства (3) образуют промежуток (а; 2), где а 2
а =
Ответ:  x + 9a 3 ) = x имеет ровно два корня.
x + 9a 3 ) = x имеет ровно два корня.
Ответы:
-
при а 16.06.2009
Задачи с параметром
Решите уравнение (ax+3=0) при всех значениях параметра (a) .
Уравнение можно переписать в виде (ax=-3) . Рассмотрим два случая:
1) (a=0) . В этом случае левая часть равна (0) , а правая – нет, следовательно, уравнение не имеет корней.
2) (ane 0) . Тогда (x=-dfrac<3>) .
(a=0 Rightarrow xin varnothing; \ ane 0 Rightarrow x=-dfrac<3>) .
Решите уравнение (ax+a^2=0) при всех значениях параметра (a) .
Уравнение можно переписать в виде (ax=-a^2) . Рассмотрим два случая:
1) (a=0) . В этом случае левая и правая части равны (0) , следовательно, уравнение верно при любых значениях переменной (x) .
2) (ane 0) . Тогда (x=-a) .
(a=0 Rightarrow xin mathbb
Решите неравенство (2ax+5cosdfrac
Неравенство можно переписать в виде (axgeqslant -dfrac<5><4>) . Рассмотрим три случая:
1) (a=0) . Тогда неравенство принимает вид (0geqslant -dfrac<5><4>) , что верно при любых значениях переменной (x) .
2) (a>0) . Тогда при делении на (a) обеих частей неравенства знак неравенства не изменится, следовательно, (xgeqslant -dfrac<5><4a>) .
3) (a . Тогда при делении на (a) обеих частей неравенства знак неравенства изменится, следовательно, (xleqslant -dfrac<5><4a>) .
(a=0 Rightarrow xin mathbb
Решите неравенство (a(x^2-6) geqslant (2-3a^2)x) при всех значениях параметра (a) .
Преобразуем неравенство к виду: (ax^2+(3a^2-2)x-6a geqslant 0) . Рассмотрим два случая:
1) (a=0) . В этом случае неравенство становится линейным и принимает вид: (-2x geqslant 0 Rightarrow xleqslant 0) .
2) (ane 0) . Тогда неравенство является квадратичным. Найдем дискриминант:
Т.к. (a^2 geqslant 0 Rightarrow D>0) при любых значениях параметра.
Следовательно, уравнение (ax^2+(3a^2-2)x-6a = 0) всегда имеет два корня (x_1=-3a, x_2=dfrac<2>) . Таким образом, неравенство примет вид:
[(ax-2)(x+3a) geqslant 0]
Если (a>0) , то (x_1 и ветви параболы (y=(ax-2)(x+3a)) направлены вверх, значит, решением являются (xin (-infty; -3a]cup big[dfrac<2>; +infty)) .
Если (a , то (x_1>x_2) и ветви параболы (y=(ax-2)(x+3a)) направлены вниз, значит, решением являются (xin big[dfrac<2>; -3a]) .
(a=0 Rightarrow xleqslant 0; \ a>0 Rightarrow xin (-infty; -3a]cup big[dfrac<2>; +infty); \ a .
При каких (a) множество решений неравенства ((a^2-3a+2)x -a+2geqslant 0) содержит полуинтервал ([2;3)) ?
Преобразуем неравенство: ((a-1)(a-2)x geqslant a-2) . Получили линейное неравенство. Рассмотрим случаи:
1) (a=2) . Тогда неравенство примет вид (0 geqslant 0) , что верно при любых значениях (x) , следовательно, множество решений содержит полуинтервал ([2;3)) .
2) (a=1) . Тогда неравенство примет вид (0 geqslant -1) , что верно при любых значениях (x) , следовательно, множество решений содержит полуинтервал ([2;3)) .
3) ((a-1)(a-2)>0 Leftrightarrow ain (-infty;1)cup (2;+infty)) . Тогда:
(xgeqslant dfrac<1>
(dfrac<1>
Учитывая условие (ain (-infty;1)cup (2;+infty)) , получаем (ain (-infty;1)cup (2;+infty)) .
(xleqslant dfrac<1>
Действуя аналогично случаю 3), получаем (ain (1; dfrac<4><3>big]) .
Определить количество корней уравнения (ax^2+(3a+1)x+2=0) при всех значениях параметра (a) .
Рассмотрим два случая:
1) (a=0) . Тогда уравнение является линейным: (x+2=0 Rightarrow x=-2) . То есть уравнение имеет один корень.
2) (ane 0) . Тогда уравнение является квадратным. Найдем дискриминант: (D=9a^2-2a+1) .
Рассмотрим уравнение (9a^2-2a+1=0) : (D’=4-36 , следовательно, уравнение (9a^2-2a+1=0) не имеет корней. Значит, выражение ((9a^2-2a+1)) принимает значения строго одного знака: либо всегда положительно, либо отрицательно. В данном случае оно положительно при любых (a) (в этом можно убедиться, подставив вместо (a) любое число).
Таким образом, (D=9a^2-2a+1>0) при всех (ane 0) . Значит, уравнение (ax^2+(3a+1)x+2=0) всегда имеет два корня: (x_<1,2>=dfrac<-3a-1pm sqrt D><2a>)
Параметрические уравнения
Уравнение, которое кроме неизвестной величины содержит также другую дополнительную величину, которая может принимать различные значения из некоторой области, называется параметрическим. Эта дополнительная величина в уравнении называется параметр . На самом деле с каждым параметрическим уравнением может быть написано множество уравнений. Мы рассмотрим модуль параметрического уравнения и решение простых параметрических уравнений.
Задача 1 Решите уравнения в отношении к $x$
A) $x + a = 7$
B) $2x + 8a = 4$
C) $x + a = 2a – x$
D) $ax = 5$
E) $a – x = x + b$
F) $ax = 3a$
A) $x + a = 7 Leftrightarrow x = 7 – a$, то есть решение к данному уравнению найдено.
Для различных значений параметров, решения есть $x = 7 – a$
B) $2x + 8a = 4 Leftrightarrow 2x = 4 – 8a Leftrightarrow x = 2 – 4a$
C) $x + a = 2a – x Leftrightarrow x + x = 2a – a Leftrightarrow 2x = a Leftrightarrow x = frac<2>$
D) $ax = 5$, когда а отличается от 0 мы можем разделить обе части на a и мы получим $x = 5$
Если $a = 0$, мы получим уравнение, такое как $0.x = 5$, и которое не имеет решения;
E) $a – x = x + b Leftrightarrow a – b = x + x Leftrightarrow 2x = a – b Leftrightarrow x = frac
F) Когда a = 0 уравнение ax = 3a равно 0.x = 0
Поэтому, любое x является решением. Если a отличается от 0, тогда
$ax = 3a Leftrightarrow x = frac<3a> Leftrightarrow x = 3$
Задача 2 Если a является параметром, решите уравнение:
A) $(a + 1)x = 2a + 3$
B) $2a + x = ax + 4$
C) $a^2x – x = a$
D) $a^2x + x = a$
A) Если $a + 1$ отлично от 0, то есть.. $a neq -1$,
тогда $x = frac<2a+3>
если $a + 1 = 0$, i.e. $a = – 1$
уравнение принимает вид $0cdot x = (2)cdot(-1) + 3 Leftrightarrow$
$0cdot x = 1$, что не имеет решения;
B) $2a + x = ax + 4 Leftrightarrow$
$x – ax = 4 – 2a Leftrightarrow$
$(1 – a)cdot x = 2(2 – a)$
Если $(1 – a) neq 0$, то есть a $neq 1$; решение будет
$x = frac<2(2 - a)><(1 - a)>$;
Если $a = 1$ уравнение примет вид $0cdot x = 2(2 – 1) Leftrightarrow$
$0cdot x = 2$, что не имеет решения
C) $a^2x – x = a Leftrightarrow$
$x(a^2 -1) = a Leftrightarrow$
$(a – 1)(a + 1)x = a$
Если $a – 1 neq 0$ и $a + 1 neq 0$ то есть $a neq 1, -1$,
решением есть is $x = frac<(a - 1)(a + 1)>$
Если $a = 1$ or $a = -1$, уравнение принимает вид is $0cdot x = pm 1$, что не имеет решения
D) $a^2x + x = a Leftrightarrow$
$(a^2 + 1)x = a$
В этом случае $a^2 + 1 neq 0$ для любого $а$, потому что это есть сумма позитивного числа (1) и одного негативного числа
$(a^2 geq 0)$ поэтому $x = frac
Задача 3 Если a and b являются параметрами, решите уравнения:
A) $ax + b = 0$
B) $ax + 2b = x$
C) $(b – 1)y = 1 – a$
D) $(b^2 + 1)y = a + 2$
B) $ax + 2b = x Leftrightarrow ax – x = -2b Leftrightarrow (a – 1)x = -2b$
Если $a – 1 neq 0$, i.e. $a neq 1$, решение есть is $x = -frac<2b>
Если $a – 1 = 0$, то есть $a = 1$, и $b neq 0$, уравнение принимает вид $0cdot x = – 2b$ и не имеет решения
C) Если $b – 1 neq 0$, то есть $b neq 1$,
решением есть $y = frac<1-a>
Если $b – 1 = 0$, то есть $b = 1$, но $1 – a neq 0$,
то есть $a neq 1$, уравнение принимает вид $0cdot y = 1 – a$ и не имеет решения.
Если $b = 1$ и $a = 1$ уравнение принимает вид $0cdot y = 0$ и любое $y$ является решением
D) $b^2 + 1 neq 0$ для любого $b$(почему?), поэтому
$y = frac
Задача $4$ Для каких значений $x$ следующие выражения имеют равные значения :
A) $5x + a$ и $3ax + 4$
B) $2x – 2$ и $4x + 5a$
Чтобы получить одинаковые значения мы должны найти решения уравнений
$5x + a = 3ax + 4$ и $2x – 2 = 4x + 5a$
A) $5x + a = 3ax + 4 Leftrightarrow$
$5x – 3ax = 4 – a Leftrightarrow$
$(5 – 3a)x = 4 – a$
Если $5 – 3a neq 0$, т.e. $a neq frac<5><3>$, решения есть $x = frac<4-a><5-3a>$
Если $5 – 3a = 0$, т.e. $a = frac<5><3>$, уравнение принимает вид $0cdot x = 4 – frac<5> <3>Leftrightarrow$
$0cdot x = frac<7><3>$, что не имеет решения
B) $2x – 2 = 4x + 5a Leftrightarrow$
$-2 – 5a = 4x – 2x Leftrightarrow$
$2x = – 2 – 5a Leftrightarrow$
$x = -frac<2+5a><2>$
Задача 5 Решите параметрическое уравнение:
A) $|ax + 2| = 4$
B) $|2x + 1| = 3a$
C) $|ax + 2a| = 3$
A) $|ax + 2| = 4 Leftrightarrow ax + 2 = 4$ или $ax + 2 = -4 Leftrightarrow$
$ax = 2$ или $ax = – 6$
Если $a neq 0$, уравнения примут вид $x = frac<2>$ or $x = -frac<6>$
Если $a = 0$, уравнения не имею решения
B) Если $a 0$, это эквивалентно $2x + 1 = 3a$
или $2x + 1 = -3a Leftrightarrow 2x = 3a – 1 Leftrightarrow x = frac<3a-1><2>$ or
$2x = -3a – 1 Leftrightarrow x = frac<3a-1> <2>= -frac<3a-1><2>$
C) $|ax + 2a| = 3 Leftrightarrow ax + 2a = 3$ или $ax + 2a = – 3$,
и мы находим $ax = 3 – 2a$ или $ax = -3 – 2a$
Если a = 0, тогда нет решений, если $a neq 0$
решениями есть: $x = frac<3-2a>$ и $x = -frac<3+2a>$
Задача 6 Решите уравнение $2 – x = 2b – 2ax$, где a и b являются действительными параметрами. Найдите, для каких значениях a уравнение имеет в качестве решения натуральное число, если $b = 7$
Представим данное уравнение в следующем виде: $(2a – 1)x = 2(b – 1)$
Возможны следующие варианты:
Если $2a – 1 neq 0$, т.e. $a neq frac<1><2>$, уравнение имеет единственное решение
$x = frac<2(b-1)><2a-1>$
Если $a = frac<1><2>$ и $b = 1$, уравнение получает вид $0cdot x = 0$ и любое $x$ является решением
Если $a = frac<1><2>$ и $b neq 1$, мы получаем $0cdot x = 2(b – 1)$, где $2(b – 1) neq 0$
В этом случае уравнение не имеет решения.
Если $b = 7$ и $a neq frac<1><2>$ является единственным решением
$x = frac<2(7-1)> <2a-1>= frac<12><2a-1>$
Если a целое число, тогда $2a – 1$ также есть целым числом и решением есть
$x = frac<12><2a-1>$ является натуральным числом когда
$2a – 1$ есть положительным делителем для числа $12$.
Чтобы a было целым числом, делитель числа $12$ должен быть нечетным. Но только $1$ и $3$ являются положительными нечетными числами, на которые делится12
Поэтому $2a – 1 = 3 Leftrightarrow a = 2$ или $2a – 1 = 1 Leftrightarrow$
$a = 1 a = 2$ или $2a – 1 = 1 Leftrightarrow a = 1$
Задача 7 Решите уравнение $|ax – 2 – a| = 4$, где a является параметром. Найдите, для каких значениях а корнями уравнения являются целые отрицательные числа.
Из определения модуля мы получаем
$|ax – 2 – x| = 4 Leftrightarrow ax – 2 – x = 4$ или $ax – 2 – x = – 4$
Из первого равенства мы получаем $x(a – 1) – 2 = 4 Leftrightarrow$
$(a – 1)x = 4 + 2 Leftrightarrow (a – 1)x = 6$
Из второго равенства мы получаем $(a – 1)x = -2$
Если $a – 1 = 0$, т.e. $a = 1$, последнее уравнение не имеет решения.
Если $a neq 1$ мы находим, что $x = frac<6>
Чтобы эти корни были целыми отрицательными числами, должно выполняться следующее:
Для первого равенство $a – 1$ должно быть отрицательным делителем 6, и для второго – положительным делителям 2
Тогда $a – 1 = -1; -2; -3; – 6$ или $a – 1 = 1; 2$
Мы получаем $a – 1 = -1 Leftrightarrow a = 0; a – 1 = -2 Leftrightarrow$
$a = -1; a – 1 = -3 Leftrightarrow a = -2; a – 1 = -6 Leftrightarrow a = -5$
или $a – 1 = 1 Leftrightarrow a = 2; a – 1 = 2 Leftrightarrow a = 3$
Тогда $a = -5; -2; -1; 0; 2; 3$ являются решениями задачи.
Задача 8 Решите уравнение:
A) $3ax – a = 1 – x$, где a это параметр;
B) $2ax + b = 2 + x$, где a и b являются параметрами
A) $3ax + x = 1 + a Leftrightarrow (3a + 1)x = 1 + a$.
Если $3a + 1 neq 0$, т.e. $a neq -11 /3 /3$ , решение есть
$x = frac<1+a><3a+1>$
Если $a = -frac<1><3>$ уравнение принимает вид $0cdot x = frac<1.1><3>$, что не имеет решения.
B) $2ax – x = 2 – b Leftrightarrow (2a – 1)x = 2 – b$
Если $2a – 1 neq 0$, т.e. $a neq frac<1><2>, x = frac<2-b><2a-1>$ является решением.
Если $a = frac<1><2>$ уравнение принимает вид $0.x = 2 – b$
Тогда, если $b = 2$, любое x является решением, если $b neq 2$, уравнение не имеет решения.
Задача 9 Дано уравнение $6(kx – 6) + 24 = 5kx$ , где к – целое число. Найдите, для каких значений k уравнение:
A) имеет корень $-frac<4><3>$
B) не имеет решения;
C) имеет корень как натуральное число.
Перепишем уравнение в виде $6kx – 36 + 24 = 5kx Leftrightarrow kx = 12$
A) Если $x = -frac<4><3>$, для k мы получим уравнение $-frac<4> <3k>= 12 Leftrightarrow k = – 9$
B) Уравнение $kx = 12$ не имеет решения, когда $k = 0$
C) Когда $k neq 0$ является корнем $x = frac<12>
Задача 10 Решите уравнение:
A) $2ax + 1 = x + a$, где a является параметром;
B) $2ax + 1 = x + b$, где a и b являются параметрами.
A) $2ax + 1 = x + a Leftrightarrow 2ax – x = a – 1 Leftrightarrow$
$(2a – 1)x = a – 1$
Если $2a – 1 neq 0$, т.e. $a neq frac<1><2>$, единственным решением уравнения является
$x = frac
Если $2a – 1 = 0$, т.e. $a = frac<1><2>$, уравнение принимает вид
$0.x = frac<1><2>– 1 Leftrightarrow 0.x = -frac<1><2>$, что не имеет решения
B) $2ax + 1 = x + b Leftrightarrow$
$2ax – x = b – 1 Leftrightarrow$
$(2a – 1)x = b – 1$
Если $2a – 1 neq 0$, т.e. $a neq frac<1><2>$, решением является
$x = frac
Если $a = frac<1><2>$, уравнения эквивалентно $0.x = b – 1$
Если b = 1 любое x является решением, если $b neq 1$ тогда нет решения.
Задача 11 Дано уравнение $3(ax – 4) + 4 = 2ax$, где параметром является целым числом. Найдите, для каких значений a уравнение в качестве корней имеет:
А) $left(-frac<2><3>right)$
B) целое число
C) натуральное число
A) Если $x = -frac<2><3>$ есть решением уравнения, тогда должно быть истинным
$3left[aleft(-frac<2><3>right) – 4right] + 4 = 2aleft(-frac<2><3>right) Leftrightarrow$
$-2a – 12 + 4 = -frac<4a> <3>Leftrightarrow$
$frac<4a> <3>– 2a = 8 Leftrightarrow frac<4a-6a> <3>= 8 Leftrightarrow$
$-frac<2a> <3>= 8 Leftrightarrow a = -12$
C) Чтобы получить натуральное (целое положительное) число для этого решения $x=frac<8>$ число должно равняться: $a=1, 2, 4, 8$
Задача 12 Дано уравнение $2 – x = 2b – 2ax$, где $a$ и $b$ – параметры. Найдите, для каких значений a уравнение имеет решения в виде натурального числа, если $b = 7$
В уравнение мы подставляем $b = 7$ и получаем $2 – x = 2.7 – 2ax Leftrightarrow$
$2ax – x = 14 – 2 Leftrightarrow (2a – 1)x = 12$
Если $2a -1 neq 0$, т.e. $a neq frac<1><2>$, уравнение примет вид
$x = frac<12><2a-1>$ и это будет натуральное число, если знаменатель $2a – 1$ есть положительным делимым $12$ и кроме того, чтобы оно было целым числом, необходимо, чтобы $2a – 1$ было нечетным числом.
Поэтому $2a – 1$ может быть $1$ или $3$
Из $2a – 1 = 1 Leftrightarrow 2a = 2 Leftrightarrow a = 1$ и $2a – 1 = 3$
$Leftrightarrow 2a = 4 Leftrightarrow a = 2$
Задача 13 Дана функция $f(x) = (3a – 1)x – 2a + 1$, где a – параметр. Найдите, для каких значений a график функции:
А) пересекает ось абсцисс;
B) пересекает ось абсцисс
Чтобы график функции пересёк ось абсцисс, необходимо, чтобы
$(3a – 1)cdot x -2a + 1 = 0$ имело решения и не имело решения для непересечения оси абсцисс.
С уравнения мы получаем $(3a – 1)x = 2a – 1$
Если $3a – 1 neq 0$, т.e. $a neq frac<1><3>$, уравнение имеет решения
$x = frac<2a-1><3a-1>$, поэтому график функции пересекает ось абсцисс.
Если $a = frac<1><3>$, мы получаем $0.x = frac<2> <3>– 1 Leftrightarrow 0.x = -frac<1><3>$, что не имеет решения.
Поэтому, если $a = frac<1><3>$, график функций не пересекает ось абсцисс.
Задача 14 Решите параметрическое уравнение:
A) $|x -2| = a$
B) $|ax -1| = 3$
C) $|ax – 1| = a – 2$
A) Если $a 0$ мы получаем:
$|x – 2| = a Leftrightarrow x – 2 = a$ или $x – 2 = -a$
Из $x – 2 = a Rightarrow x = a + 2$, и из
$x – 2 = -a Rightarrow x = 2 – a$
Если $a = 0$, тогда $x – 2 = 0$ или $x = 2$
B) $|ax – 1| = 3 Leftrightarrow ax – 1 = 3$ или $ax – 1 = -3$
откуда $ax = 4$ или $ax = – 2$
Если $a neq 0$ решения: $x = frac<4>$ or $x = -frac<2>$
Если $a = 0$, здесь нет решения
C) Если $a – 2 0$, т.e. $a > 2$ мы получаем
$|ax – 1| = a – 2 Leftrightarrow ax – 1 = a – 2$ или $ax – 1 = 2 – а$
Итак, мы получаем $ax = a – 1$ или $ax = 3 – a$
Потому что $a > 2, a neq 0$, therefore
$x = frac
Если $a = 2$, уравнения эквивалентно
$2x – 1 = 0 Leftrightarrow 2x = 1 Leftrightarrow x = frac<1><2>$
Задача 15 Найдите, для каких значений параметра m (a), два уравнения эквивалентны:
A) $frac
B) $frac
C) $|3 – x| + x^2 -5x + 3 = 0$ и $ax + 2a = 1 + x$, если $x > 3$
A) Решим второе уравнение. Запишем его в виде:
$(-x – 1)^2 – 1 = x^2 Leftrightarrow$
$[(-1)(x + 1) ]^2 – 1 = x^2 Leftrightarrow$
$x^2 + 2x + 1 – 1 = x^2 Leftrightarrow$
$2x = 0 Leftrightarrow x = 0$
Для первого мы получим
$frac
Эти два уравнения эквивалентны, если они имеют одинаковые корни, т.e.
$2 – 3m = 0 Leftrightarrow$ $m = frac<2><3>$
B) Для первого уравнения решением есть $х = 2 – 3m$ и для второго мы получим
$x – m = 3 – 6m Leftrightarrow$ $x = 3 – 5m$
Они имеют одинаковые корни, когда
$2 – 3m = 3 – 5m Leftrightarrow 5m – 3m = 3 – 2 Leftrightarrow 2m = 1 Leftrightarrow m = frac<1><2>$
X Международная студенческая научная конференция Студенческий научный форум – 2018








ПРИЁМЫ И МЕТОДЫ РЕШЕНИЯ ЗАДАЧ С ПАРАМЕТРОМ
- Авторы
- Файлы работы
- Сертификаты
Что означает «решить задачу с параметром»?
Как начинать решать такие задачи? И что означает «решить параметрическую задачу»? Прежде всего, надо сделать то, что делается при решении любого уравнения или неравенства: привести заданное уравнение (неравенство) к более простому виду, например, разложить рациональное выражение на множители, разложить тригонометрический многочлен на множители, избавиться от модулей, логарифмов, и т.д. Решая такие задания нужно множество раз обращаться к его текстовой части с целью выполнения сформулированного там условия.
Проще говоря, решить задачу с параметром – значит указать, при каких значениях параметров существуют решения и каковы они.
Каковы основные типы задач с параметрами?
1. Уравнения (неравенства), которые надо решить либо для любого значения параметра, либо для значений параметра, принадлежащих заранее оговоренному множеству.
Например: При каких значениях параметра уравнение имеет единственный корень?
2. Уравнения (неравенства), для которых необходимо определить количество решений в зависимости от значения параметра.
Например: При каких уравнение имеет ровно три корня?
3. Уравнения (неравенства), для которых требуется найти все значения параметра, при которых указанные уравнения (неравенства) имеют заданное число решений ( или не имеют решений, или имеют бесконечно много решений).
Например: Найдите все значения параметра а при каждом из которых уравнение -13а+5 имеетровно два корня.
4. Уравнения (неравенства), для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.
Например: При каких значениях уравнение имеет ровно одно решение на промежутке
Каковы основные способы (методы) решения задач с параметром?
Способ I (аналитический). Это способ применения стандартных операций при решении уравнений (неравенств) без параметра, он же, на мой взгляд, и самый трудный. При решении заданий аналитическим способом требуется знать большой объем математической информации и уметь грамотно это применять.
Привем решение задания с параметром, которое решается аналитическим способом:
Найдите все значенияа, при каждом из которых уравнение имеет хотя бы один корень.
Рассмотрим функции и
1.Пусть , тогда (раскрываем модуль со знаком минус) , . Получаем, что угловой коэффициент функции равен 4 либо 12, (так как может быть одинаковый знак в зависимости от числа х.) При таких значениях график функции возрастает (так как коэффициент больше 0)
2.Пусть , тогда , Получаем, что угловой коэффициент функции равен -4 либо -12. При таких значениях график функции убывает (так как коэффициент меньше 0)
3.При х=0, тогда Получаем, что = Функция возрастает при и убывает при , поэтому =
Исходное уравнение имеет один корень, когда
откуда , либо , где а=-5.
Ответ: -5,
Способ II (графический). Наиболее понятный и очень наглядный способ решения. Суть его заключается в том, что в зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a). Естественно, что для этого просто необходимо знать типы элементарных функций (степенные, показательные, логарифмические, тригонометрические, обратные тригонометрические), их свойства и графики (кстати, в ВУЗах эта тема в курсе высшей математики изучается одной из первых) Использование графического способа даже схематически помогает найти решение задачи. Решая задания графическим способом, я сделала следующее наблюдение: если в правой и левой части уравнения (неравенства) находятся функции разных типов, то можно смело утверждать, что решение аналитическим способом такой задачи бессмысленно, не нужно тратить на него время, а лучше сразу же создать графическую иллюстрацию задания. Наглядно и быстро!
Приведу пример задания 18 ЕГЭ, которое очень легко решается этим способом:
Найдите все значенияа, при каждом из которых уравнение имеет единственный корень.
Запишем уравнение в виде и рассмотрим две функции и .
Рассмотрим функцию , преобразовывая подкоренное выражение, получим:
. Таким образом, получаем.функцию, графиком которой является полуокружность с радиусом 2 в центре с точкой (-1;0), лежащей в верхней полуплоскости.
Графиком функции является прямая с угловым коэффициентом -а, проходящая через точку М (4;2)
Уравнение имеет единственный корень, если графики функций имеют одну общую точку (т.е. прямая касается или пересекает полуокружность в единственной точке).
Рассмотрим рисунок: 1. Прямая МС является касательной к полуокружности, следовательно, МС и полуокружность пересекаются в единственной точке. Так как МС параллельна оси ОХ ( У точки М (4,2) и С(-1,2)), то угловой коэффициент равен нулю. Таким образом, найдено первое значение а=0, при котором уравнение имеет один единственный корень.
2. Проведем прямую через точки М(4;2) и А(-3;0) ( так как координаты известны). Прямая МА пересекает график полуокружности в двух точках, но такая ситуация не удовлетворяет условию задачи. Поэтому надо найти значения углового коэффициента, при которых вышеназванное условие не выполняется. Чтобы найти значения –а подставим координаты точек М и А в функцию.
Получаем, -а=0 и а=.
При условии прямые имеют с графиком две общие точки, а это не удовлетворяет условию задачи.
3. Проведем прямую МВ через точки М(4;2) и В(1;0). Чтобы найти значения –а подставим координаты точек М и А в функцию.
Получаем –а= и –а=. При условии прямые имеют с графиком одну общие точки и это удовлетворяет условию задачи.Ответ: а=0,
Способ III (решение относительно параметра). При решении этим способом переменные x и a принимаются равноправными и выбирается та переменная, относительно которой аналитическое решение признается более простым. После проведенных упрощений возвращаются к исходному смыслу переменных x и a и заканчивают решение.
Ниже представлено решение параметрического задания данным способом:
3.При всех значениях параметра а решить уравнение: |х + 3| – a|x – 1| = 4.
Найдем значения х, при которых выражения, стоящие под знаком модуля обращаются в ноль. Получили х= -3 и х=1. Разобьем числовую прямую на 3 части полученными точками и решим 3 системы: 1) , если . Найденный будет решением, если .
2) , если . Найденный удовлетворяет нужному неравенству, следовательно, является решением при . Если же , то решением является любой .
В данной работе рассмотрены способы и приёмы решения задач с параметром. По нашему мнению наиболее эффективным является графический метод решения задач с параметром.
Корянов А.Г., Прокофьев А.А. Уравнения и неравенства с параметрами.
 =
=  ;
; ;
; ;
; ;
; ;
;
 ;
;





