Равнодействующая плоской системы сил

Равнодействующая плоской системы сил. Теорема Вариньона

Плоская система приводит к силе. Теорема вариньона позволяет любой плоской системе сил F2 воздействовать на твердые тела…И Fn>. Эта система применяется к произвольно выбранному центру C: GGL=2^K>и основным векторам, имеющим моменты, равные n M

C=^MC (FK) относительно этого центра. Затем представьте себе, самый главный момент, с — * =я _ _ Стержень представлен в виде модуля главного вектора системы, то есть пары сил, равных Frn=F=F'(представляющих их через F и F’).

Для этого нужно изменить плечи этой пары так, чтобы момент был равен MS, воспользовавшись Людмила Фирмаль

тем, что пара может быть передана любым способом с точки зрения ее действия, например, F’t помещается в центр C и он помещается в направлении, противоположном действию вектора RGL (4.3). Вторая сила F, составляющая соединенную пару, должна быть обозначена таким образом, чтобы знак момента относительно центра С и знак главного момента совпадали(рис. 4.3 они положительны). Тогда плечи этой пары будут равны: h=Mc / Frn=Mc / F. (4.5) Таким образом,плоская

система этой силы эквивалентна силе FrJi и паре(F, F’), но так как силы GGL и F ‘ уравновешены, то данная система может проходить через центр убывающей CJ. Таким образом, если основной вектор данной плоской силовой системы не равен нулю, то эта система, в результате, направлена в равном с основным вектором направлении и в равном направлении.: ^RAVN=^GL=2Fk,(4-6) А=1 Докажем теорему в момент получения результата, принадлежащего французскому

механику Варину-ОНУ. .Три.* Айрис рис. 4.3. 4.4 Момент любой плоской системы, полученный в результате действия силы на любой центр (точку), являющийся теоремой, равен алгебраической сумме моментов всех сил этой системы на один и тот же центр. Доказательство основано на предыдущей теореме: результирующий момент равен, приложенный в точке C к центру редукции C: M SS^равно)=/?Этикетка (см. Фигура. 4.3), между тем, из Формула (4.5)ясно, что МС является главной точкой системы сил относительно

центра с, учитывая формулу (4.4), имеем ^c (f p a8H)=i^c(f*) — (4.7) / g=1 Теорема вариньона широко используется при решении различных задач статики. В частности, он используется при определении результатов параллельных сил. Сила называется параллельной, если ее линии действия параллельны друг другу. Найти результат действия двух параллельных сил Fi и F2, действующих на твердое тело(рис. 4.4). Исходя из Формулы (1.6), модуль главного вектора планарной системы принимает вид F[=]/F2rJ1X+P

L y. x=2k=i п/?GL y=FKy. Используя тот факт, что оси могут быть- L=1 Однако, чтобы расположить плоскость произвольно, мы направляем ось

x так, чтобы она была перпендикулярна силовым линиям Fi и F2/, а ось y Людмила Фирмаль

параллельна им. Далее, учитывая, что основным вектором является остаток 36равнодействующей, параллельной и направленной в одном направлении, 2^KX=0, к=I Y]F go-fpaBH — ________________k = л =2^K u1+^2. Затем запишем сумму сил для любой точки, лежащей на прямой BiB2 или ее продолжении, по теореме Вариньона найдем положение линии действия равным^FpaBH. Возьмем точку как центр момента, который мы имеем: L4B1 (Pravn)==m B1 (L)+M B1(F2), с тех пор MBl(Fl)=0, (F1+F2) B[C=F2BiB2 или F1B1C=^2^2^ * (4.8)

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

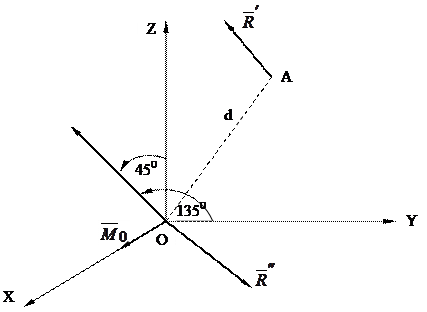
Теорема Вариньона о моменте равнодействующей пространственной системы

Эта теорема связана с моментом равнодействующей пространственной сходящейся системы сил относительно произвольной точки. Ее сформулировал и смог доказать великий французский ученый Пьер Вариньон (1654-1722).

Теорема гласит следующим образом:

Момент равнодействующей пространственной системы сходящихся сил относительно произвольной точки равен векторной сумме моментов всех слагаемых сил относительно этой же точки.

Действительно, если совокупность всех 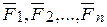сил, действующих на абсолютно твердое тело сходится в некоторой точке О, то ее равнодействующая находится как геометрическая сумма этих сил, т.е.:

= =

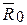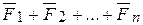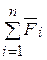
и приложена в той же точке О (рис.4.3.).

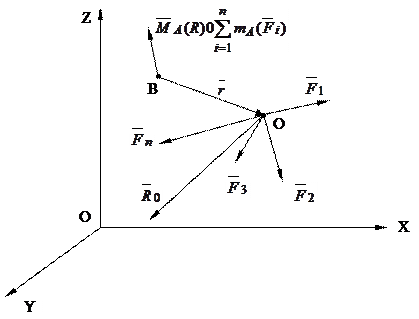Возьмем произвольную точку А и обозначим через 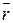вектор-радиус точки О относительно точки А. Тогда по определению момента равнодействующей находим:

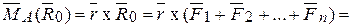
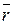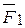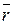=( х 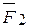)+( 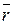х )+…+( х ) =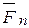

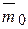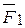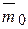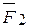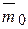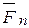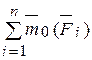= ( )+ ( )+…+ ( )= . (4.21)

Подчеркнем, что теорема Вариньона верна только для сходящейся системы сил и для совокупности сил с параллельными друг другу линиями действия.

Если все силы 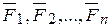лежат на некоторой плоскости и составляют плоскую систему сходящихся сил, то вместо геометрической суммы моментов берется алгебраическая сумма моментов этих сил, т.е.

M( 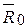)= 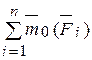(4.22)

Следует заметить, что формулы (4.21) и (4.22) применяются во многих задачах инженерных дисциплин.

Вопросы для самопроверки

1. Приведите силу, параллельно самой себе, к заданному центру.

2. Как можно сформулировать теорему Пуансо?

3. Что такое главный вектор?

4. Что такое главный момент?

5. Чему равна величина главного вектора?

6. Как находится величина главного момента?

7. Как находится направление главного вектора?

8. Определите направление главного момента системы сил.

9. Какой угол между собой составляет главный вектор и главный моменты системы сил?

10. Как находятся проекции главного вектора на оси координат x, y, z?

11. Определите проекции главного момента на оси координат x, y, z.

12. Какие возможные частные случаи вы знаете при приведении системы сил к заданному центру?

13. Как в векторной форме выглядят условия равновесия произвольной пространственной системы сил?

14. Как записываются они в координатной форме?

15. Какие частные случаи условия равновесия вы знаете?

16. Как можно сформулировать теорему Вариньона?

ЗАДАЧИ:

I. К вершинам куба со стороной а приложены силы F₁ = F₂ = 5 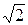. Приведите эти силы к простейшему виду (рис.4.4).

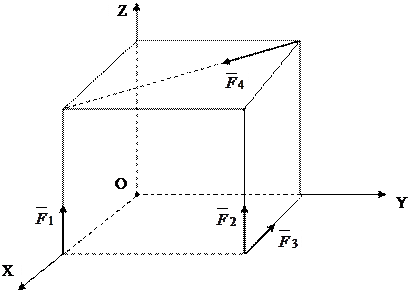
Решение: Оси декартовых координат x,y,z направим как на рис.4.3. Тогда проекции главного вектора на эти оси, согласно (4.4) будут:

R_x= 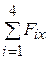= -F₃ + F₄cos 45 0 = 0

R_y= 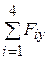= -F₄cos45 0 = -10 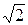H.

R_z= 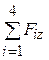= F₁ + F₂ = 10 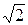H.

R= 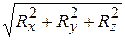= 20 H.

Так как R_x = 0, то 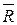лежит на плоскости YOZ. Через направляющие косинусы (4.6) находится направление главного вектора:

cos( 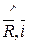)= =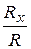0, 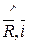=90 0 ,

cos( 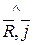)= =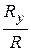- 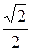, 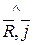=135 0 ,

cos( 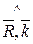)= = 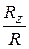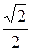, 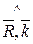=45 0 .

Аналогичным образом формулу (4.10), применив к этой задаче, находим главный моменты системы сил.

M_x= 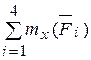= F₂a + F₄ acos 45 0 = 15 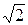a Н×м

M_y= 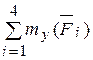= -F₁ a – F₂a + F₄ acos 45 0 = 0,

M_z= 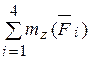= F₃a – F₄ acos 45 0 = 0.

Тогда согласно (4.11) находим:

M= 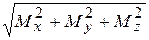=15 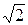a Н × м.

Так как M_y = 0, M_z = 0, то главный момент приложенных сил к кубу будет напралвен по оси Х.

Следовательно при приведении указанных сил к центру О система заданных сил сводится к главному вектору R=20 Н, направления которого определяются углами 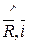= 90 0 , 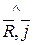=135 0 , 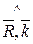=45 0 и главному моменту M = 15 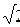a нм, направленному по оси Х (рис.4.5), т.е. 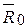^ . В этом случае система сил приводится к равнодействующей 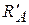, приложенной в точке А, где

OA = d = = .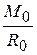

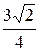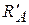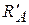Но = R и || R.

II. Определить опорные силы реакции для конструкции и силу , которая держит конструкции в равновесии, показанной на рис.4.6. При этом даны: Q = 3000 H; G = 2000 H; a = 0,6 м; b = 0,2 м; с = 0,4 м; r = 0,05 м; a = 30 0 ; b = 60 0 .

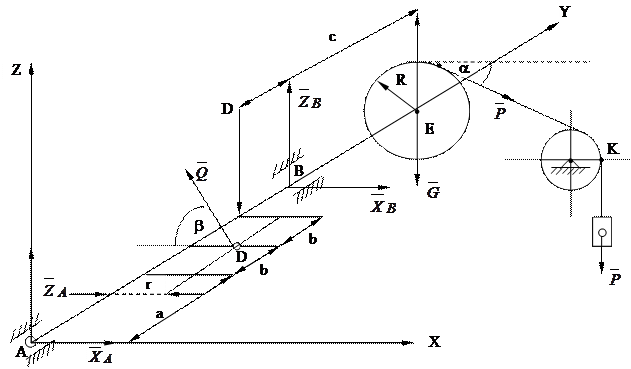
Решение. На рисунке приведены все активные и пассивные силы. Причем через 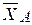, 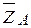? 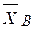, 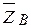соответственно обозначен силы реакции в цилиндрических подшипниках А и В. Тогда согласно уравнений равновесия (4.18)

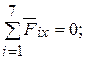X_A – Qcos 60 0 + X_B + Pcos 30 0 = 0,

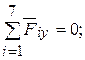0 = 0,

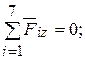Z_A + Qcos 30 0 + Z_B – Pcos 60 0 – G = 0,

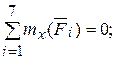(a + b) Qcos 30 0 + (a + 3b) Z_B – (a + 3b + c) Pcos 60 0 – (a + 3b + c) G = 0,

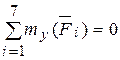; -rQ cos 30 0 + R × P = 0,

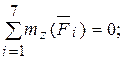(a + b) Qcos 60 0 – (a + 3b) X_B + (a + 3b + c) × Pcos 30 0 = 0

Решив совместно эти уравнения, находим:

P= 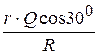= 649,5 H.

X_B = 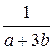[(a + b) Qcos 60 0 + (a + 3b + c) × Pcos 30 0 ] = 1750 H.

X_A = Qcos 60 0 – X_B – Pcos 30 0 = -812 H.

Z_B= 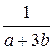[(a + 3b + c) (Pcos 60 0 + G) – (a + b) Qcos 30 0 ] = 1368 H.

Z_A = -Qcos 30 0 – Z_B + Pcos 60 0 + G 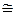355 H.

Таким образом определены все неизвестные X_A, Z_A, X_B, Z_B и Р, удерживающие указанную конструкцию в равновесии.

Теорема Вариньона (геометрия)

Теоре́ма Вариньо́на — геометрический факт, доказанный Пьером Вариньоном:

Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника.

Середины сторон произвольного четырёхугольника — вершины параллелограмма

Параллелограмм, образованный серединами сторон, иногда называется вариньоновским или вариньоновым.

Центр параллелограмма Вариньона лежит на середине отрезка, соединяющего середины сторон исходного четырёхугольника (в этой же точке пересекаются отрезки, соединяющие середины противоположных сторон — диагонали вариньоновского параллелограмма).

Площадь параллелограмма Вариньона равна половине площади исходного четырёхугольника.

Следствие из теоремы: для прямоугольника и равнобедренной трапеции параллелограммом Вариньона является ромб, а для ромба — прямоугольник.

Проведём диагональ AC. Отрезки EF и GH будут средними линиями треугольников и . По теореме о средней линии, отрезки будут параллельны диагонали, а, значит, и друг другу. Повторив аналогичные рассуждения для диагонали BD, получаем, что противоположные стороны четырёхугольника EFGH параллельны, и, по определению, это — параллелограмм.

Доказательство, что площадь параллелограмма равна половине площади исходного четырехугольника: Пусть диагональ проходит внутри четырёхугольника. Тогда площадь треугольника равна , где — высота треугольника , проведённая из вершины . Аналогично, площадь треугольника равна . Тогда площадь всего четырёхугольника равна . Но — это сумма расстояний до прямой от точек и , то есть в точности высота параллелограмма . А поскольку сторона параллелограмма вдвое меньше , то и площадь параллелограмма равна половине площади , Q. E. D.

Теорема Вариньона – определение, формулировка, доказательство

Цель: исследовать приемы решений планиметрических задач с использованием теоремы Вариньона и следствий из нее.

1.Изучить теорему Вариньона.

2.Сравнить решение планиметрических задач ,применяя теорему Вариньона и традиционный способ решения.

3.Сравнить затраченные временные ресурсы на решение задач с помощью теоремы Вариньона и обычным способом.

4.Практически применить в решении олимпиадных задач и задач ОГЭ и ЕГЭ теоремы Вариньона.

Гипотеза: решать планиметрические задачи с помощью теоремы Вариньона намного эффективнее по сравнению с традиционным способом.

Актуальность: новейшие технологии в математический дисциплинах требуют применения прогрессивных и эффективных способов решения задач.

Объект исследования: параллелограмм Вариньона, бимедианы четырехугольника, теорема Вариньона и ее свойства

Предмет исследования: планиметрические задачи

Методы исследования:

1.Анализ, систематизация и обобщение данных из различных источников информации.

2.Самостоятельное решение задач.

В математике самыми трудными считаются геометрические задачи. Почти каждая геометрическая задача нестандартна. Надо подумать, какие нужно сделать дополнительные построения, какими воспользоваться теоремами, при этом очень непросто из их огромного количества выбрать ту, которая наилучшим образом поможет в решении.

2.Теорема Вариньона и её доказательство.

Пьер Вариньон— французский математик и механик. Обучался в иезуитском колледже и университете в Кане, где стал магистром в 1682 году. Основной вклад Вариньон совершил в статику и механику. В 1687 году в своей работе «Проект новой механики…» Вариньон дал точную формулировку закона параллелограмма сил, развил понятие момента сил и вывел теорему, получившую имя Вариньона.

Теорема Вариньона

Четырехугольник, образованный путем последовательного соединения середин сторон выпуклого четырехугольника, является параллелограммом, и его площадь равна половине площади данного четырехугольника.

ABCD – выпуклый четырехугольник

AK=KB; BL=LC; CM=MD; AN=ND

1) KLMN – параллелограмм;

2) S KLMN = S ABCD:2

Доказательство:

1. Рассмотрим одну из сторон четырехугольника KLMN, например KL. KL – средняя линия треугольника ABC (по определению),следовательно, KL ∥ AC. Аналогично, так как MN – средняя линия треугольника ADC,то MN ∥ AC. Так как KL ∥ AC и MN ∥ AC следовательно, KL ∥ NM и KL=MN=AC:2. Таким образом, KLMN – параллелограмм. Этот параллелограмм называется параллелограммом Вариньона данного четырехугольника.

2. Средняя линия треугольника отсекает от него треугольник, площадь которого в четыре раза меньше площади исходного треугольника,

3. т . е . S KBL = S ABC:4, S MDN=S ADS:4. Следовательно , S 1+S 3=S ABCD:4. Аналогично , S 2+S 4= S ABCD:4. Следовательно , S 1+S 3 + S 2+S 4 = S ABCD :4 + S ABCD:4 = S ABCD:2.

Т . е ., S KLMN = S ABCD:2. Что и требовалось доказать.

3. Свойства параллелограмма Вариньона :

1. Каждая пара противоположных сторон параллелограмма Вариньона параллельна диагонали в исходном четырехугольнике.

2. Сторона параллелограмма Вариньона вдвое короче диагонали в исходном четырехугольнике, к которому он параллелен.

3. Площадь параллелограмма Вариньона равна половине площади исходного четырехугольника. Это верно для выпуклых, вогнутых и скрещенных четырехугольников при условии, что площадь последнего определяется как разность площадей двух треугольников, из которых он состоит.

4. Периметр параллелограмма Вариньона равен сумме диагоналей исходного четырехугольника.

5. Диагонали параллелограмма Вариньона – это бимедианы исходного четырехугольника.

Определение: Бимедианы четырехугольника – это отрезки, соединяющие середины противоположных сторон (диагонали параллелограмма Вариньона)

4. Следствия из теоремы Вариньона.

Следствие 1: Параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны 2) бимедианы перпендикулярны.

Дано: ABCD – четырехугольник; KLMN – параллелограмм Вариньона; AC=BD

Доказать: KLMN – ромб

Доказательство: Так как AC=BD (диагонали исходного четырехугольника равны по условию), то стороны параллелограмма Вариньона будут равны KL=LM=MN=NK (используя свойство средних линий треугольников, образованных при пересечении диагоналей исходного четырехугольника). Параллелограмм c равными сторонами является ромбом.

Следствие 2: Параллелограмм Вариньона является прямоугольником тогда и только тогда, когда в исходном четырехугольнике: 1) диагонали перпендикулярны; 2) бимедианы равны

Дано: четырехугольник ABCD; KLMN – параллелограмм Вариньона; диагонали AC и BD – перпендикулярны

Доказать: KLMN – прямоугольник

Доказательство: Так как диагонали AC и BD – перпендикулярны, то стороны параллелограмма Вариньона будут перпендикулярны. Следовательно, параллелограмм Вариньона является прямоугольником.

Следствие 3: Параллелограмм Вариньона является квадратом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны и перпендикулярны; 2) бимедианы равны и перпендикулярны

Дано: четырехугольник ABCD; KLMN – параллелограмм Вариньона; диагонали AC и BD – перпендикулярны; AC=BD

Доказать: KLMN – квадрат

Доказательство : Так как диагонали исходного четырехугольника AC и BD равны и перпендикулярны, то стороны параллелограмма Вариньона будут равны и перпендикулярны. Следовательно, параллелограмм Вариньона является квадратом.

5. Основная часть работы. Применение теоремы Вариньона при решении задач.

Эффективность и удобство применения теоремы Вариньона рассмотрю на задачах , которые я составила сама и подобрала из сборников ОГЭ прошлых лет.

Докажите, что если диагонали четырехугольника равны, то его площадь равна произведению средних линий .

Дано: ABCD – четырехугольник; AC = BD

Доказать: S ABCD = KM*LN

Доказательство: Так как диагонали AC = BD, параллелограмм Вариньона является ромбом, площадь ромба равна половине произведения его диагоналей. Что и требовалось доказать.

Найдите площадь четырехугольника ABCD ,если его диагонали равны 12 см и 14 см , а его бимедиана равняется 9 см

Решение: 1)построим внутри ABCD параллелограмм Вариньона – MKNP

По теореме Вариньона SMKNP= 0,5SABCD

Т.к. бимедиана является диагональю параллелорамма MKNP =) она разделяет параллелограмм на 2 треугольника- PMK и PNK =)

2)MK = 0,5 BD т.к. BD является средней линией треугольника DAB = 7см

PM = 0,5 AC т.к. является средней линией треугольника ADC = 6см

3) По теореме Герона S=√p(p-a)(p-b)(p-c),где p=a+b+c/2- полупериметр треугольника =11см

SMKNP = √11(11-7)(11-6)(11-9)=√11*4*5*2=√440=2√110*2 =4√110 =)

Ответ :SABCD =8√110см

Докажите , что площадь параллелограмма ,образованного прямыми , проходящими через вершины выпуклого четырехугольника и параллельными его диагоналям , в два раза больше площади исходного четырехугольника

Так как AMOL,MONB,CKON,DKOL-параллелограммы , то

Отсюда получаем , что SABCD=2SKLMN,что и требовалось доказать.

В четырехугольнике ABCD обозначены точки E и F – середины диагоналей AC и BD соответственно. Докажите , что SELFN T1T2 ,

А T1T2=0,5AC- противоречие

Если же E=T1,то T1С=0,5AC=T1T2 , чего также быть не может.

3) Значит, точка Е лежит внутри KLMN .

Аналогично показываем , что точка F лежит внутри параллелограмма KLMN.

Тогда SELFN , SABCD = SABC+SACD=S+S=2S

Одна из средних линий четырехугольника ABCD равна а . Его диагонали равны 3/2а и 5/2а. Найдите площадь четырехугольника ABCD.

Решение : 1)Пусть в четырехугольнике ABCD LN =a, AC=3/2a,BD=5/2a.

Тогда , KL=1/2AC=3/4a и KN=1/2BD=5/4a

2) По формуле Герона площадь треугольника KLN = √3/2a*a/2*3a/4*a/4=3a²/8

В четырехугольнике отрезки , соединяющие середины противоположных сторон , равны. Докажите , что диагонали исходного четырехугольника перпендикулярны.

Доказательство: для доказательства будем использовать теорему Вариньона

▲DAC =) EF||HG||AC. Аналогично со сторонами EH и FG

2) Т.к. EG=FH, то из этого следует , что четырехугольник EFGH является параллелограммом Вариньона и прямоугольником (следствие2) =) EF⊥EH, FG⊥GH

▲BAC =) EF||AC и ▲AEH

Поэтому EF⊥EH и AC⊥BD ч.т.д.

Докажите , что сумма длин двух отрезков , соединяющих середины противоположных сторон произвольного четырехугольника , меньше суммы длин его диагоналей

1) Рассмотрим произвольный четырехугольник ABCD , где точки K,L,M,N – середины сторон AB,BC,CD,AD

2) NM является средней линией для▲ADC ,а LK средняя линия для▲ABC =)NM||CA||LK . Аналогично с ▲CDB и ▲ADB =) ML||DB||NK

3) NM=LK=1/2CA и ML=NK=1/2DB(по свойству средней линии ▲) =)

4) т.к. сторона должна быть меньше суммы двух других=) KM Geretschlager , R . Kalinowski Jozef , Svrcek Jaroslav A Central European Olympiad , The Mathematical Duel [ электронный ресурс] / R . Geretschlager , J . Kalinowski , J . Svrcek .-2018.- Vol . 7. – Режим доступа : ht tps://books.google. com . –Загл. с экрана.

14. Bits of Math [ Электронныйресурс ]. – community blogs ,2015-.- Режим доступа : https://artofproblemsolving.com, свободный.- Загл.с экрана.

15. Russia 2004 problem [ Электронныйресурс ]. – community blogs ,2011-.- Режим доступа : https :// artofproblemsolving . com , свободный.- Загл.с экрана.

Применение теоремы Вариньона к решению задач

2. 2. Применение теоремы Вариньона к решению задач.

Рассмотрим применение теоремы Вариньона к решению планиметрических задач повышенной трудности. Дело в том, что планиметрические задачи на олимпиадах встречаются значительно чаще.

Мы будем называть параллелограмм KLMN параллелограммом Вариньона, а отрезки КМ и LN, соединяющие середины противоположных сторон четырёхугольника АВСD – средними линиями этого четырёхугольника.

Задача 1. В выпуклом пятиугольнике ABCDE середины сторон AB и CD, BC и DE соединены отрезками. K, L – середины этих отрезков. Доказать, что отрезок KL параллелен пятой стороне AE и составляет ¼ от неё.

Решение: отрежем четырёхугольник ABCD и пусть Р-середина AD, тогда по теореме Вариньона A1B1C1P – параллелограмм, А1С1 – его диагональ и К – середина А1С1, значит, К – середина и второй

диагонали параллелограмма В1Р. Значит, KL – средняя линия треугольника PB1D1, поэтому KL||PD1 и KL=1/2 PD1, но PD1 – средняя линия треугольника ADE, значит, PD1||AE и PD1=1/2AE, поэтому KL||AE и KL=1/4 AE.

Задача 2. Верно ли, что можно составить треугольник из любой средней линии треугольника и отрезков, вдвое меньших его диагоналей?

Решение: верно, так как параллелограмм Вариньона существует для любого выпуклого четырёхугольника. Например, условию задачи удовлетворяют треугольники KLM и LMN на рис. 10. рис. 10

Задача 3. Средние линии четырёхугольника ABCD равны a и b, а угол между ними 60˚. Найдите диагонали четырёхугольника.

Решение: пусть KM=a, LN=b, (рис. 10). Тогда NM=, а LT=.

Из треугольника LTM по теореме косинусов . Но LM= BD, поэтому , откуда BD=. Аналогично из треугольника TNM найдём MN, потом вычислим AC: AC=.

Ответ: ;

Задача 4. Докажите, что сумма квадратов диагоналей четырёхугольника в два раза больше суммы квадратов его средних линий.

Доказательство: в параллелограмме Вариньона, как и в любом другом параллелограмме, сумма квадратов рис. 11 диагоналей равна сумме квадратов всех его сторон, т. е. Учитывая, что KL=1/2 AC и LM= 1/2 BD (рис. 11), получим: KM2+LN2=1/2(AC2+BD2), AC2+BD2=2(KM2+LN2).

Задача 5. Докажите, что площадь параллелограмма Вариньона равна половине площади четырёхугольника ABCD.

Доказательство: (рис. 12).

Учитывая, что , KL=1/2 AC и KN=1/2 BD, получим: рис. 12

Задача 6. Докажите, что все четырёхугольники, имеющие общие середины

Доказательство: действительно, для всех таких четырёхугольников определён один и тот же параллелограмм Вариньона. Его площадь равна половине площади каждого из исходных четырёхугольников (задача 5), тем самым их равновеликость доказана.

Задача 7. Докажите, что если диагонали четырёхугольника равны, то его площадь равна произведению средних линий.

Доказательство: в случае равенства диагоналей AC и BD параллелограмм Вариньона KLMN является ромбом (рис. 13), а рис. 13

площадь ромба равна половине произведения диагоналей:

, тогда .

Задача 8. Диагонали четырёхугольника ABCD равны d1 и d2, а средние линии равны между собой. Найдите площадь четырёхугольника.

Решение: из условия задачи следует, что в параллелограмме Вариньона диагонали KM и LN равны (рис. 12). Значит, KLMN – прямоугольник и SKLMN=1/2 d1d2, а с другой стороны, SKLMN=1/2 SABCD, следовательно, SABCD=1/2d1d2.

Ответ: SABCD=1/2d1d2.

Задача 9. Докажите, что площадь четырёхугольника равна произведению средней линии на одну из диагоналей и на синус угла между ними.

Доказательство: согласно рис. 14 необходимо доказать, рис. 14

что . Треугольник KLN представляет собой половину параллелограмма Вариньона. (). Так как KL=1/2AC, то , значит, , а с другой стороны, (см. задачу 8), тогда .

Задача 10. Докажите, что сумма квадратов сторон четырёхугольника равна сумме квадратов его диагоналей, сложенной с учетверённым квадратом отрезка, соединяющего середину его диагоналей.

Доказательство: согласно рис. 11 надо доказать, что. Для медианы ET треугольника ELN имеем: , где , , откуда . Аналогично, выразив медиану FT треугольника KFM и учитывая, что и , получим: .

Кроме того, (задача 7).

Итак, получаем: , откуда:

Задача 11. Постройте трапецию по диагоналям, одному из углов и отрезку, соединяющему середины оснований.

Решение: пусть в трапеции ABCD, которую необходимо построить, известны длины диагоналей AC и BD, отрезка LN и величина угла А (рис. 15).

Поскольку и , нетрудно построить по трём рис. 15

сторонам треугольник KLN. Далее построим его до параллелограмма Вариньона. Затем на отрезке KN построим сегмент, вмещающий угол А, и проведём через точку N параллельно KM прямую, она пересечёт сегмент в точке А. Дальнейшее построение очевидно.

В ходе работы мы прорешали более двадцати пяти задач, формулировки и решения наиболее интересных из них дополнительно приведены в приложении. Мы убедились в том, что теорема Вариньона помогает красиво, оригинально решать задачи, открывать и доказывать новые свойства четырёхугольников.

“Исследование применения параллелограмма Вариньона при решении сложных задач”

Актуальность данной темы заключается в том, что в последние годы в России, стало проводиться много различных математических олимпиад. Различных форм: очные, заочные, дистанционные и т.д.. Я являюсь активной участницей традиционных школьной и районной олимпиад , краевой многопредметной олимпиады «Интеллект», Всероссийского « Молодежного чемпионата» и « Талантливой молодежи».

Моё стремление углублять математические знания по математике является главной причиной работы над проектом и выбором темы «Исследование значимости параллелограмма Вариньона при решении сложных задач».

Данные проводимого мною исследования являются дополнением и углублением изученного материала в курсе геометрии, а применение опыта полученного при решении планиметрических задач с использованием параллелограмма Вариньона и следствий из нее помогают решать сложные задачи.

Цель работы: исследовать доказательство теоремы Вариньона и показать, что теорема надежный помощник в решении геометрических задач.

Просмотр содержимого документа
«”Исследование применения параллелограмма Вариньона при решении сложных задач” »

1.Провести теоретико – методический анализ научной литературы по проблематике исследования.

2.Изучить теорему Вариньона ,ее следствия и применение для разных видов четырехугольников ( выпуклых, вогнутых, пространственных).

3. Исследовать применение теории при решении не стандартных задач.

Объектом исследования является – система научных открытий французского математика Пьера Вариньона.

Гипотеза: параллелограмм Вариньона – надежный помощник в решении задач.

Предметом исследования являлись энциклопедии, словари, научная литература, Интернет.

Основными методами исследования были поиск, наблюдение, описание.

1.1Исследование исторических событий создания параллелограмма Вариньона.

Создателем знаменитого параллелограмма Вариньона является французский механик и математик, член Парижской академии наук, профессор Пьер Вариньон( 1654 -22.12.1722г, Париж).

Труды профессора коллежа Мазарии ( с 1688г), профессора коллеж де Франс ( с 1704г), посвящены теоретической механике, анализу бесконечно малых и геометрии.

Он был одним из первых ученых, ознакомивших Францию с анализом бесконечно малых. Вариньон руководил « Журналом ученых».

В геометрии Пьер Вариньон изучал различные специальные линии, написал учебник по элементарной геометрии ( издан в 1731).

Главные заслуги его были представлены в Парижскую Академию наук в работе « Проект новой механики…», Вариньон дал точную формулировку закона параллелограмма сил. Развил понятие момента сил и вывел очень важную теорему, позволяющую решать сложные геометрические задачи более простыми методами, так называемая теорема Вариньона. Он первым обратил внимание на, казалось бы, довольно очевидный факт: середины сторон произвольного четырехугольника являются вершинами параллелограмма. В дальнейшем полученный параллелограмм назвали параллелограммом Вариньона.

И я постараюсь всех убедить, что параллелограмм Вариньона – надежный помощник при решении трудных, в том числе и олимпиадных задач.

Глава 2.Основные теоретические сведения.

2.1 Исследование теоремы и следствия из теоремы Пьера Вариньона.

2.2 Исследование применения теоремы для выпуклых и невыпуклых четырехугольников.

2.3 Исследование применения параллелограмма Вариньона для самопересекающейся замкнутой ломаной

Для аналитических рассуждений и решений сложных задач, с использование разных видов четырехугольников мною были изучены следующие теоретические сведения открытые Пьером Вариньоном.

Бимедианы четырехугольника – это отрезки, соединяющие середины противоположных сторон.

Рис.1 (см. в приложении )

1. Рассмотрим одну из сторон четырехугольника KLMN, например KL. Так как KL является средней линией треугольника ABC, то KL || AC. По тем причинам MN|| AC. Следовательно, KL||NM и KL=MN=AC/2. таким образом, – параллелограмм. Этот параллелограмм называется параллелограммом Вариньона данного четырехугольника.

2 . Средняя линия треугольника отсекает от него треугольник, площадь которого в четыре раза меньше площади исходного треугольника. Поэтому сама сумма площадей первого и третьего треугольников равна четверти площади всего четырехугольника. То же и относительно суммы площадей второго и четвертого треугольников. Поэтому площадь параллелограмма KLMN составляет половину площади четырехугольника ABCD

В целях совершенствования доступности рассуждений при решении олимпиадных задач я предлагаю использовать следующее:

3. Следствия из теоремы Вариньона.

Следствие 1. Параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике диагонали равны и бимедианы перпендикулярны.

Следствие 2.Бимедианы четырехугольника и отрезок, соединяющий середины диагоналей, пересекаются в одной точке и делятся этой точкой пополам.

Следствие 3. ( теорема Эйлера) Для четырехугольника сумма квадратов всех сторон равна сумме квадратов диагоналей плюс учетверенный квадрат отрезка, соединяющего середины диагоналей.

Следствие 4 ( теорема о бабочках). Суммы площадей накрест лежащих четырехугольников, образованных пересечением бимедиан выпуклого четурехугольника равны.

Результатом этого этапа исследования является то, что теорема Вариньона и её следствия применяются для различных видов четырехугольника: выпуклых , самопересекающихся четырехугольных замкнутых ломаных, тетраэдра, пространственных четырехугольников и т.д.

Поэтому изученный материал позволит решить мне получить необходимую информацию для решения , ее структуру; составить план решения; сделать необходимые расчеты; проанализировать . Все это способствует эффективному решению.

2.4.Применение теоремы Вариньона при решении сложных ( олимпиадных) задач.

Постройте ромб с вершинами на сторонах прямоугольника ABCD.

Поскольку диагонали прямоугольника равны, то параллелограмм Вариньона для прямоугольника ABCD и будет искомым ромбом KLMN.

Рис (см. в презентации )

Докажите, что площадь параллелограмма Вариньона KLMN равна половине площади четырехугольника ABCD.

Доказательство.

S ABCD=1/2AC*BD*sin(угла 1).

S KLMN=KL*KN*sin(угла 2)

Учитывая, что угол первый равен углу второму и KL=1/2AC, KN=1/2BD, получим необходимое.

Рис. (см. в презентации)

Задача 3. Докажите, что сумма квадратов диагоналей четырёхугольника в два раза больше суммы квадратов его средних линий.

В параллелограмме Вариньона, как и в любом другом параллелограмме, сумма квадратов диагоналей равна

сумме квадратов всех его сторон, т.е.

Учитывая, что KL=1/2 AC и LM= 1/2 BD

KM 2 +LN 2 =1/2(AC 2 +BD 2 ),

AC 2 +BD 2 =2(KM 2 +LN 2 ).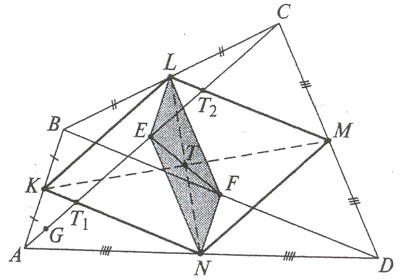

Уравнение биссектрисы в треугольнике — формула, свойства и решение задач

Треугольник является одной из самых простых фигур, которая часто встречается школьникам в задачах по геометрии. В свою очередь, биссектриса представляет собой важный элемент, характеризующий тот или иной угол. Решение геометрических проблем с участием этих объектов требует наличия определенных знаний. Чтобы уметь составлять по координатам вершин уравнение биссектрисы треугольника, необходимо понимать выражения для прямых линий.

Прямая на плоскости

Задачи по геометрии могут относиться к одному из двух принципиально отличающихся случаев. Это следующие:

На плоскости, где достаточно двух координат для описания любых геометрических объектов.

В трехмерном пространстве, где любая точка имеет три координаты.

Когда рассматривают треугольники и их элементы, то в ряде ситуаций речь идет именно о двумерном пространстве. В нем всякая прямая линия может быть выражена в виде нескольких математических форм или уравнений. Чаще всего используются следующие типы:

Общий. Он также называется универсальным. Прямая представляет собой следующую математическую запись: A*x + B*y + C = 0. Здесь A, B, C — числовые коэффициенты, x и y — переменные, являющиеся координатами. Сразу нужно отметить, что эта форма представления прямой используется для составления уравнения биссектрисы угла. Для удобства геометрического изображения общую форму записи часто представляют в виде y = f (x). Нужно понимать, что указанной форме в пространстве соответствует не прямая, а плоскость.

Канонический или уравнение в отрезках. Имеет оно такой вид: y/p + x/q = 1. Здесь p, q — это координаты, в которых прямая пересекает оси y и x, соответственно, поэтому удобно ее изображать в координатной системе.

Векторный. Это один из важных типов представления прямой как на плоскости, так и в пространстве. По сути, он является исходным представлением, из которого можно получить все остальные. Математически он записывается так: (x, y) = (x0, y0) + α*(v1, v2). Где (x0, y0) — координаты произвольной точки, которая лежит на прямой, (v1, v2) — направляющий вектор, он параллелен заданной прямой, α — произвольное число, параметр.

Параметрический. Этот тип представляет собой систему уравнений, которую удобно использовать во время преобразования одного вида прямой в другой. Представляет он собой следующую математическую запись: x = x0 + α*v1; y = y0 + α*v2. Несложно понять, что, выражая параметр α, можно получить уравнения общего вида и в отрезках. Объединяя же систему уравнений в одно выражение, получается векторная форма записи прямой.

Делящая пополам угол линия

Каждый школьник, который знаком с азами геометрии, знает, что прямая, делящая на две равные части произвольный угол, называется биссектрисой. Этот элемент присутствует для любой фигуры, которая в своем составе содержит какой-либо угол.

Другое определение биссектрисы гласит, что она представляет собой геометрическое расположение точек, которые равноудалены от соответствующих сторон углового объекта. Например, если имеется угол dac, то любая из точек биссектрисы находится на одинаковом расстоянии как от отрезка da, так и от отрезка ac.

Способы построения

В классах общеобразовательных школ рассматривают два основных способа построения биссектрисы. Это следующие:

С помощью транспортира. Для этого следует измерить заданный угол в градусах, разделить его пополам. Полученное значение отметить в виде точки. Затем соединить вершину угла и поставленную точку внутри него. Получится искомый элемент.

С использованием циркуля и линейки. Эти инструменты еще проще применять для построения биссектрисы, чем транспортир. Сначала необходимо установить в вершину угла ножку циркуля и отметить дугами пересечение окружности со сторонами. Затем, в точки пересечения поставить ножку циркуля и провести две окружности. Соединив две точки их пересечения одной прямой, можно получить биссектрису.

Имеется еще один метод, который позволяет просто начертить изучаемый линейный элемент. Для его использования нужна линейка со шкалой. С помощью нее следует от вершины угла отмерить два одинаковых отрезка любой длины. Затем соединить концы этих отрезкой, получится равнобедренный треугольник.

В нем любая биссектриса также является высотой и медианой. Поэтому, разделив его ровно пополам линейкой, и соединив полученную точку с вершиной, можно получить требуемую линию.

Основные свойства

Чтобы найти по координатам вершин длину биссектрисы треугольника, следует знать некоторые свойства этого геометрического объекта. Главным из них является существование двух линий, которые делят пополам исходный угол. Нужно понимать, что угол бывает не только внутренний, но и внешний. По сути, оба типа образуются при пересечении двух прямых. Нетрудно доказать, что биссектрисы каждого из них пересекаются всегда под углом 90 °.

Еще одним важным свойством является тот факт, что пересекаются в одной точке биссектрисы треугольника. Она представляет собой центр вписанной в фигуру окружности. Чтобы это доказать, следует вспомнить, что каждая точка биссектрисы равноудалена от соответствующих сторон угла.

Пусть имеется треугольник ABC. У него две биссектрисы пересекаются в точке O. Пусть это будут линии для углов A и B. Расстояние от O до AC должно быть равно таковому от O до AB. С другой стороны, расстояния от O до AB и до BC также одинаковые. Поэтому дистанции от O до BC и до AB также равны, а значит, точка O лежит на биссектрисе угла C и центром вписанной окружности является.

В треугольнике рассматриваемый геометрический элемент используется часто для решения задач благодаря применению так называемой теоремы биссектрис. Чтобы ее сформулировать максимально простым языком, следует представить, что имеется треугольник произвольного типа ABC. В нем проведена биссектриса AD, где точка D лежит на прямой BC. Тогда справедливо следующее выражение:

Это равенство не является очевидным, однако, оно было известно еще древнегреческим мыслителям. Эту теорему в несколько иной форме можно встретить в знаменитом труде по геометрии Евклида, который называется «Элементы». Доказательство равенства несложно провести с использованием небольших дополнительных построений и применением признаков подобия треугольников.

Наконец, отрезок биссектрисы, который заключен между вершиной и противоположной стороной треугольника, имеет определенную длину. Вычислить ее можно с использованием следующего равенства:

Это равенство прописано для угла A треугольника ABC, в котором противоположная A сторона имеет длину a. Стороны AB и AC имеют длины c и b, соответственно. Буквой p обозначен полупериметр фигуры.

Важно понимать, если нарисовать прямоугольный параллелепипед (или иную фигуру) в пространстве, и построить биссектрису для его граней, она будет представлять собой не прямую, а плоскость.

Уравнение биссектрисы треугольника

Когда известно, как математически записывать выражения для прямых, и что такое биссектриса, и какими свойствами она обладает, можно переходить к непосредственному нахождению ее уравнения.

В общем случае задача решается в результате применения следующей последовательности действий (существуют онлайн-ресурсы, позволяющие решить данную проблему):

Сначала требуется определить уравнения двух сторон угла по их координатам. Это легко сделать в векторной форме, а затем, преобразовать ее в выражение общего типа.

Далее, необходимо найти уравнение биссектрис первого координатного угла, прировняв расстояния от ее точек до соответствующей стороны. Рабочая формула имеет вид: |A1*x + B1*y + C|/(A1 2 + B1 2 )^0,5 = |A2*x + B2*y + C|/(A2 2 + B2 2 )^0,5. Следует обратить внимание на наличие двух различных решений этого равенства, поскольку в числителе стоит модульное выражение. Два полученных уравнения говорят о наличии взаимно перпендикулярных биссектрис для углов треугольника внутреннего и внешнего.

Для внутреннего угла искомое уравнение можно найти, если определить точку пересечения соответствующей прямой с противоположной исходному углу стороной треугольника. Та точка, сумма расстояний от которой до концов отрезка будет равна длине стороны, принадлежит искомой биссектрисе.

Пример решения задачи

Пусть, треугольник задан координатами A (1, -1), B (0, -2), C (3,0). Следует уравнение биссектрисы найти для угла B и ее длину вычислить.

Сначала нужно написать уравнения прямых для сторон AB и CB, получается:

AB: (x, y) = (1, -1) + α*(-1, -1) ==> y — x + 2 = 0;
CB: (x, y) = (3, 0) + α*(-3, -2) ==> 3*y — 2*x + 6 = 0.

Составить уравнения биссектрис можно так:

| y — x + 2 |/(2)^0,5 = | 3*y — 2*x + 6 |/(13)^0,5.

Решение этого уравнения приводит к следующим двум выражениям для взаимно перпендикулярных биссектрис:

y*(6−3*3 0,5 ) + x*(3*3 0,5 −4)+12−6*3 0,5 = 0;
y*(3*3 0,5 +6) -x*(4+3*3 0,5 )+12+6*3 0,5 = 0.

Чтобы определить, какая из двух прямых является искомой для треугольника заданного, следует точку пересечения каждой из них со стороной AC найти. Уравнение для AC имеет вид:

Подставляя его в каждое из выражений для биссектрис, можно получить две точки пересечения:

D1 = (-0,2515;-1,6258);
D2 = (1,556;-0,722).

При этом длина основания AC составляет 2,236 единицы через единичный вектор. Расстояние от точек D1 и D2 до A, C равно:

D1A = 1,4; D1C = 3,635;
D2A = 0,621; D2C = 1,614.

Видно, что точка пересечения второй прямой D2 лежит между A и C, поэтому соответствующее ей уравнение биссектрисы является ответом на задачу. Ее длину можно вычислить по формуле для модуля вектора BD2:

BD2 = 2,014 единицы.

Таким образом, для определения в треугольнике биссектрисы уравнения по координатам следует уметь находить векторную форму выражений для прямой по координатам двух точек. Также нужно знать свойства делящей пополам угол линии.