Уравнения с параметром - классификация и формулы, решение задач

IV. Каковы основные способы (методы) решения задач с параметром?

III. Какие основные типы задач с параметрами?

II. Что означает «решить задачу с параметром»?

Это зависит от вопроса в задаче.

Если, например, требуется решить уравнение, неравенство, их систему или совокупность, то это означает предъявить обоснованный ответ либо для любого значения параметра, либо для значения параметра, принадлежащего заранее оговоренному множеству.

Если же требуется найти значения параметра, при которых множество решений уравнения, неравенства и т. д. удовлетворяет объявленному условию, то, очевидно, решение задачи и состоит в поиске указанных значений параметра.

Тип 1. Уравнения, неравенства, их системы и совокупности, которые необходимо решить либо для любого значения параметра (параметров), либо для значений параметра, принадлежащих заранее оговоренному множеству.

Тип 2. Уравнения, неравенства, их системы и совокупности, для которых требуется определить количество решений в зависимости от значения параметра (параметров).

Тип 3. Уравнения, неравенства, их системы и совокупности, для которых требуется найти все те значения параметра, при которых указанные уравнения, неравенства, их системы и совокупности имеют заданное число решений (в частности, не имеют или имеют бесконечное множество решений).

Тип 4. Уравнения, неравенства, их системы и совокупности, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.

Способ I – аналитический.Это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Иногда говорят, что это способ силового, в хорошем смысле «наглого» решения.

Комментарий. По мнению авторов, аналитический способ решения задач с параметром есть самый трудный способ, требующий высокой грамотности и наибольших усилий по овладению им.

Способ II – графический. В зависимости от задачи (с переменной x и параметром a) рассматриваются графики или в координатной плоскости (x; y), или в координатной плоскости (x; a).

Комментарий. Исключительная наглядность и красота графического способа решения задач с параметром настолько увлекает изучающих тему «Задачи с параметром», что они начинают игнорировать другие способы решения, забывая общеизвестный факт: для любого класса задач их авторы могут сформулировать такую, которая блестяще решается данным способом и с колоссальными трудностями остальными способами. Поэтому на начальной стадии изучения опасно начинать с графических приемов решения задач с параметром.

Способ III – решение относительно параметра. При решении этим способом переменные x и a принимаются равноправными и выбирается та переменная, относительно которой аналитическое решение признается более простым. После естественных упрощений возвращаемся к исходному смыслу переменных x и a и заканчиваем решение.

Перейдем теперь к демонстрации указанных способов решения задач с параметром.

Задача 1. Для всех действительных значений параметра a решите уравнение

x 3 –(2–a)x 2 –ax–a(a–2)=0.

1) Исходное кубическое по x уравнение является квадратным относительно a. Поэтому, считая переменную x параметром, перепишем это уравнение в виде стандартного квадратного уравнения относительно a, опуская промежуточные шаги по раскрытию скобок и перегруппировке: a 2 –(x 2 –x+2)a – x 3 + 2x 2 = 0.

2) Поскольку x 2 –x+2=x 2 +(2–x) и –x 3 +2x 2 =x 2 (2–x), то по обратной теореме Виета

3) Поэтому исходное уравнение равносильно совокупности уравнений a=x 2 и a=2–x.

Первое уравнение преобразуется к виду x 2 =a, откуда

(1): при a 0 два решения

(3):

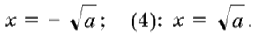
Второе уравнение совокупности имеет единственное решение (5): x=2–a для любого значения параметра a.

4) Изображаем ось параметра a и отмечаем на ней граничные значения параметра, которые фигурируют в ответах к каждому уравнению совокупности. Все найденные решения уравнений для тех значений параметра a, при которых хотя бы одно решение существует, выписываем в таблице слева (последовательно сверху вниз). Сплошной линией, параллельной оси параметра, указываем те промежутки значений параметра, при которых полученное решение существует. Заметим, что концы промежутков изображаются «светлыми» точками в случае, когда соответствующее решение не существует, а «темными» точками — в противном случае.

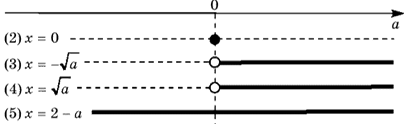
Данная развертка позволяет легко найти все решения исходного уравнения для любого действительного значения параметра: x=2–a при a 0.

5) Формирование ответа. Например, при a = 1 равенства 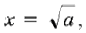и x = 2 – a определяют одно и то же значение переменной x=1, а при a=4 равенства 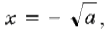и x=2–a аналогично определяют одно значение x=–2.

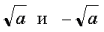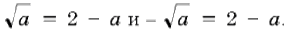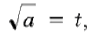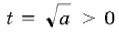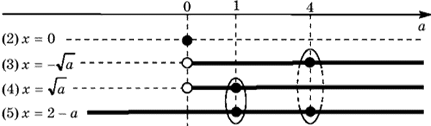
Полученные равенства (2)–(5) могут при некоторых значениях параметра a определять одно и то же значение переменной x. Найдем указанные значения параметра. Поскольку значения – различны для всех a>0, осталось выяснить, при каких значениях a выполняются равенства Пусть тогда первое уравнение приводится к виду t 2 +t–2=0, откуда t=1 и t=–2 (не подходит, так как при a > 0), т. е.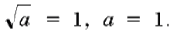. Аналогично решая второе уравнение, находим a=4.

Полученный результат в таблице 2 проиллюстрирован следующим образом: линии равенства (4) и (5) «сливаются» при a=1, линии (3) и (5) «сливаются» при a=4.

Используя таблицу 2, легко сформулировать окончательный ответ задачи.

Ответ: x=2–a при a 2 )(a+x–2)=0.

1) Исходное уравнение равносильно совокупности a–x 2 =0 или a+x–2=0.

2) Поэтому построение искомого множества точек — графика уравнения — сводится к построению графиков a=x 2 и a=2–x (рис. 1).

Уравнения с параметром – классификация и формулы, решение задач

Выделим класс задач, где за счет параметра на переменную накладываются какие- либо искусственные ограничения. Для таких задач характерны следующие формулировки: при каком значении параметра уравнение имеет одно решение, два, бесконечно много, ни одного; решением уравнения является какое-то подмножество множества действительных чисел и другие.

Прежде всего сюда относятся уравнения второй степени. Поэтому, прежде всего, обратим внимание на распространенную ошибку: считать такое уравнение квадратным. На самом деле это уравнение степени не выше второй. Пользуясь этим соображением, естественно начать решение, рассмотрев случай, когда коэффициент перед x2 равен нулю. Итак, если параметр равен нулю, то, очевидно, данное уравнение имеет единственное решение. если же a?0, то имеем дело с квадратным уравнением.

2.1 Уравнения с ограничениями для решения

Пример 1. Решить уравнение .

Решение. Данное уравнение имеет один параметр а. если a=0, то пишем линейное уравнение -4x+3=0, которое имеет один корень . При a?0 уравнение является квадратным, и его корни выражаются через параметр а формулами . Эти формулы имеют числовые значения, если: . Решая это неравенство, находим:

Ответ. При ; при , ; при корней нет.

Пример 2. Решить уравнение .

Решение. рассмотрим два случая: a=2 и a?2. В первом случае исходное уравнение принимает вид -4x+1=0. Это линейное уравнение с единственным корнем . Во втором случае получим квадратное уравнение с дискриминантом .

Найдем промежутки знакопостоянства дискриминанта.

При a=1 или a=6 дискриминант квадратного уравнения равен нулю, и оно имеет один корень , то есть при a=1 получаем корень .

При дискриминант положительный, и квадратное уравнение имеет два корня:

При дискриминант оказывается отрицательным. Следовательно, квадратное уравнение не имеет корней.

Пример 3. Решить уравнение .

Решение. . Наличие квадратного уравнения приведет к поиску корней дискриминанта. Вместе с тем условие должно привлечь внимание.

Если D>0, то есть , то уравнение имеет два корня . Если то корней нет.

Ответ. Если то , если , если , если то корней нет.

Пример 4. Решить уравнение .

Решение. Если a=-6, то решаем линейное уравнение -8x-6=0. .

Если a?-6, то решаем квадратное уравнение.

Ответ. Если , если , если , то корней нет, если , то .

Пример 5. Найти все значения параметра b, при каждом из которых уравнение имеет два различных корня.

Решение. рассматриваемое квадратное уравнение имеет два различных корня, если дискриминант его положительный. Запишем это условие: . Из последнего неравенства получим , откуда b>1.

Пример 6. Найти все значения параметра p, при каждом из которых уравнение имеет два различных корня.

Решение. Выпишем условие положительности дискриминанта данного квадратного трехчлена.

. При p=0 единственное решение.

Пример 7. Найти все значения параметра p, при каждом из которых уравнение имеет ровно одно решение.

Решение. Пусть p=0. Тогда исходное уравнение принимает вид x+2=0 и имеет единственное решение x=-2.

Пусть теперь p?0. В этом случае исходное уравнение имеет одно решение, если его дискриминант равен нулю. Получаем D=1-8p=0, откуда .

Пример 8. Найти все значения параметра p, при каждом из которых уравнение имеет одно решение.

Решение. Исходное уравнение имеет одно решение при D?0, при этом, если D=0, то уравнение имеет ровно одно решение, а при D>0 – два решения (а если есть два решения, то есть и одно). Решая неравенство .

Пример 9. При каких a уравнение имеет единственное решение ?

Решение. Понятно, что нужно начинать со случая a=2. Но при a=2 исходное уравнение вообще не имеет решений. Если a?2, то данное уравнение квадратное, и казалось бы, искомые значения параметра – это корни дискриминанта. Однако дискриминант обращается в нуль при a=2 или a=5. Поскольку мы установили, что a=2 не подходит, то a=5.

Пример 10. При каких a уравнение имеет более одного корня?

Решение. При a=0 уравнение имеет единственный корень, что не удовлетворяет условию. При a?0 исходное уравнение, будучи квадратным, имеет два корня, если его дискриминант – положителен. Отсюда получаем -4

Ответ. -4

Пример 11. При каких a уравнение имеет более одного корня?

Решение. Стандартный шаг начать со случаев a=0 и a=-3. При a=0 уравнение имеет единственное решение. Любопытно, что при a=-3 решением уравнения служит любое действительное число. При a?-3 и a?0, разделив обе части данного уравнения на a+3, получим квадратное уравнение , дискриминант которого 4(1+3a) положителен при . Опыт предыдущих промежутков показывает, что из промежутка (; надо исключить точку a=0, а в ответ не забыть включить a=-3.

2.2 Задачи на использование теоремы Виета

Пример 1. При каких значениях параметра а уравнение имеет корни, сумма которых равна нулю?

Решение. Это уравнение квадратное, его дискриминант .

Сумма корней уравнения равна – и по условию задачи она равна нулю, то есть , что возможно при . Теперь необходимо осуществить контроль неотрицательности дискриминанта при этих значениях а. при а=-2 дискриминант D=0+4*2=8 положителен, тогда как при а=1 дискриминант D=0-4=-4 оказывается отрицательным.

Пример 2. При каких значениях параметра а уравнение имеет хотя бы один положительный корень?

Решение. Данное уравнение квадратное, значит имеет корни при неотрицательном дискриминанте.

То есть при . Значение большего (или единственного, в случае нулевого дискриминанта) корня должно быть положительным: , что равносильно (при D?0) следующей совокупности условий:

То есть а 2 и а 0.

y=x|x+2a| y=x|x| y=x|x+2a|

y=a-1 y=a-1

Ясно, что при любом значении a 0 графики выглядят так, как показано на третьем рисунке. Значит, исходное уравнение имеет единственное решение при a-1>0 (то есть, при a>1); или при -a2>a-1 (и при a>0). В последнем случае решим квадратное неравенство: -a2>a-1; a2+1-1 0

a>0 a=0 a 2

y= y=t 2 -3a y=

t₁ t₂ t t₁ t t

Если теперь увеличить значение a, то часть параболы (I) сдвинется влево, а часть параболы (II)- вниз (рис.4). Уравнение по-прежнему имеет положительное решение, но оно, очевидно, больше единицы. Если же сделать значение a немного меньше нуля, то часть параболы (I) сдвинется вправо, а часть параболы (II) сдвинется вверх, и точки их пересечения начнут сближаться, причем 0 0.

Ноль в степени ноль

Ноль — наверное самое загадочное число и самое контринтуитивное. Ведь его аналога в реальной жизни просто нет. Ноль это отсутствие чего-то. Но почему ноль в степени ноль равняется единице? И главный вопрос, так ли это на самом деле? Можете проверить на своем калькуляторе до того, как прочтете…

Ноль «в степени» ноль

Как такое может быть? А вот как: 1 0 =1, 2 0 =1…. х 0 =1. Любое число при взведении в нулевую степени равняется единице. Чем сам ноль хуже? Но не все так просто.

Что означает возвести в степень? Например «два в квадрате». Что мы делаем, мы двойку умножаем на саму себя 2 раза (2*2=4), «два в кубе», двойку умножаем саму на себя 3 раза (2*2*2=8). А что если степень, это «ноль»? Нужно взять число и умножить само на себя…. ноль раз? Это странно.

Вот как выглядит график функции y=x x

Видно, что при уменьшении значения Х значение У сначала снижается, а потом начинает расти и превращается… в единицу при условии очень маленьких (почти нулевых) значениях Х. Было бы логично предположить, что когда значение уменьшится до ноля, там тоже будет единица.

Еще раз, вернемся к простым цифрам:

Что означает эта запись? Чтобы получить девять, нужно тройку умножить два раза. Правда же?

Сколько раз нужно умножить тройку саму на себя, чтобы получить единицу? А если разделить 1 на 3? Простого ответа нет? Логично, что чем больше значение степени, тем больше результат, и чем меньше это значение, тем и результат меньше.

Но на графике выше показано, что кривая «упирается» в предел, в единицу. Точнее, значение функции становится равным 1, когда ноль еще даже не достигнут. И если уменьшать Х еще больше, все равно, дальше единицы не сдвинутся.

Контекст

Как получается, что при умножении ноля самого на себя получается что-то большее самого ноля?

Если мы в реальной жизни (а не в математике) съели все яблоки и их у нас 0, то сколько бы мы не умножали отсутствующие яблоки на такие же «нулевые» фрукты, как может у нас возникнуть целое яблоко? Если вам кажется такой вопрос простым, так и есть. С одной точки зрения это странное выражение будет равняться единице, а вот с другой оно будет «не определено». То есть никакой единицы а результате умножения ноля на ноль и быть не может, да?

Математика говорит, что:

3 2 ×3 2 это тоже самое, что и 3 2+2 = 3 4 = 3 × 3 × 3 × 3= 81

4 5 ÷4 3 это тоже самое, что и 4 5–3 = 4 2 = 4 × 4 = 16

Тогда, если степени одинаковы:

3 2 ÷3 2 это тоже самое, что и 3 2-2 = 3 0 = Ой?!

Но ведь мы можем и не вычитать степени, а просто сделать две операции отдельно:

3 2 ÷3 2 это тоже самое, что и 3 2-2 = 3 0 , но 3 2 =9, тогда 3 2 ÷3 2 = 3 2-2 или 3 2 ÷3 2 =9÷9=1

А что будет если одно число поделить на самого себя? Единица!

Матанализ

С точки зрения математического анализа, все одновременно и сложно, и совсем просто. Ноль в степени ноль = неопределенность. Что, согласитесь, более логично. Ведь если у нас нет ничего и мы ничего умножим само на себя, не может же возникнуть что-то из этой пустоты?

Теория множеств

Давайте посмотрим с точки зрения теории множеств. Допустим у нас есть два множества.

Первое множество, это количество символов пароля, которым закрыт доступ к вашей страничке в соцсети, или, еще лучше, PIN код банковской карты допустим — 4 символа.

Второе множество, это количество значений, корыте может принимать каждый символ. Предположим, что это только цифры, значит цифр — 10.

Вопрос, сколько вариантов комбинаций существует? Сколько раз нужно ввести случайную комбинацию, чтобы гадать пароль? Каждый символ

10 4 =10 000 тысяч вариантов.

Можно сказать, что множество цифр (10) отображается на множестве возможных символов (4). Но есть и «пустые» множества. Например, вы не поставили пароль вовсе, у вас ноль символов, так сколько попыток понадобится, чтобы получить доступ к счету? Ровно одна.

То есть при 10 0 =1, но тоже самое случится, если пароля нет и значений тоже нет 0 0 =1. Простыми словами, ноль в степени ноль, означает, что пароль не установлен и каждое значение тоже 0. Тогда может существовать только одна такая «комбинация».

А на самом деле?

Практического применения это математическое выражение, как нетрудно догадаться, не имеет вовсе. Ни одном инженеру, ни одному экономисту не придет в голову умножать ноль на ноль ноль раз. Это просто не применимая конструкция. Так что вопрос остается в области математики, и может быть философии.

Это наверное единственный случай, когда оставаясь математиком можно для свободно для себя решать чему равно «0 в степени 0».

Возведение в степень: правила, примеры

Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.

Понятие возведения в степень

Начнем с формулирования базовых определений.

Возведение в степень – это вычисление значения степени некоторого числа.

То есть слова “вычисление значение степени” и “возведение в степень” означают одно и то же. Так, если в задаче стоит “Возведите число 0 , 5 в пятую степень”, это следует понимать как “вычислите значение степени ( 0 , 5 ) 5 .

Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.

Как возвести число в натуральную степень

Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a . Это можно записать так:

Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.

Условие: возведите – 2 в степень 4 .

Решение

Используя определение выше, запишем: ( − 2 ) 4 = ( − 2 ) · ( − 2 ) · ( − 2 ) · ( − 2 ) . Далее нам нужно просто выполнить указанные действия и получить 16 .

Возьмем пример посложнее.

Вычислите значение 3 2 7 2

Решение

Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.

Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49

Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.

Выполните возведение в квадрат числа π .

Решение

Для начала округлим его до сотых. Тогда π 2 ≈ ( 3 , 14 ) 2 = 9 , 8596 . Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ ( 3 , 14159 ) 2 = 9 , 8695877281 .

Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени ( ln 6 ) 3 или преобразовать, если это возможно: 5 7 = 125 5 .

Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:

Это понятно из записи .

От основания степени это не зависит.

Так, ( − 9 ) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 .

Как возвести число в целую степень

Для удобства разберем отдельно три случая: если показатель степени – целое положительное число, если это ноль и если это целое отрицательное число.

В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.

Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 .

5 0 = 1 , ( – 2 , 56 ) 0 = 1 2 3 0 = 1

0 0 – не определен.

У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а – любое число, а z – целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.

Возведите 2 в степень – 3 .

Решение

Используя определение выше, запишем: 2 – 3 = 1 2 3

Подсчитаем знаменатель этой дроби и получим 8 : 2 3 = 2 · 2 · 2 = 8 .

Тогда ответ таков: 2 – 3 = 1 2 3 = 1 8

Возведите 1 , 43 в степень – 2 .

Решение

Переформулируем: 1 , 43 – 2 = 1 ( 1 , 43 ) 2

Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом: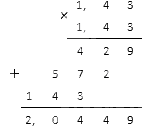

В итоге у нас вышло ( 1 , 43 ) – 2 = 1 ( 1 , 43 ) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).

Ответ: ( 1 , 43 ) – 2 = 10000 20449

Отдельный случай – возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a – 1 = 1 a 1 = 1 a .

Пример: 3 − 1 = 1 / 3

9 13 – 1 = 13 9 6 4 – 1 = 1 6 4 .

Как возвести число в дробную степень

Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n .

Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени.

У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а , потом возводим результат в степень с целым показателем m .

Проиллюстрируем на примере.

Вычислите 8 – 2 3 .

Решение

Способ 1. Согласно основному определению, мы можем представить это в виде: 8 – 2 3 = 8 – 2 3

Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 – 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4

Способ 2. Преобразуем основное равенство: 8 – 2 3 = 8 – 2 3 = 8 3 – 2

После этого извлечем корень 8 3 – 2 = 2 3 3 – 2 = 2 – 2 и результат возведем в квадрат: 2 – 2 = 1 2 2 = 1 4

Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.

Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.

Возведите 44 , 89 в степень 2 , 5 .

Решение

Преобразуем значение показателя в обыкновенную дробь: 44 , 89 2 , 5 = 44 , 89 5 2 .

А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107

Ответ: 13 501 , 25107 .

Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями – довольно сложная работа. Для нее обычно требуется вычислительная техника.

Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную – значения не имеет: 0 – 4 3 .

Как возвести число в иррациональную степень

Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.

Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:

Вычислите приближенное значение 2 в степени 1,174367.

Решение

Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 . . . ≈ 2 1 , 1743 ≈ 2 , 256833 .

Better Explained: Как понять ноль в нулевой степени?

В школе нас учат, что степень — это многократное умножение. Это прекрасно, но становится совсем непонятным, когда мы встречаем 3 1,5 или 0 0 .

Как мы можем повторить ноль нулевое количество раз и получить единицу? Всё дело в том, что наш подход к степени числа как к многократному умножению неверен. Нам нужно сменить парадигму. Давайте посмотрим, как мы привыкли воспринимать арифметические действия, и что они на самом деле из себя представляют.

Сложение

Как мы привыкли думать: это повторяющийся счёт

Как на самом деле: перемещение

Умножение

Как мы привыкли думать: это многократное сложение

Как на самом деле: масштабирование

Степень

Как мы привыкли думать: многократное умножение

Как на самом деле: рост с течением времени

Смотрим на арифметику как на преобразование

Отойдём на шаг назад. Как мы изучаем арифметику? Нас учат, что числа — это некое количество единиц; сложение — это прибавление одного количества единиц к другому количеству единиц (3+4 = 7), а умножение — это многократное сложение (2*3 = 2+2+2 = 6).

Многократное сложение прекрасно работает с круглыми числами, но что вы скажете про сложение чисел вроде -1 или 2²?

Очевидно, что эта модель восприятия неполноценна. Числа — это не просто единицы чего-то; гораздо лучше представлять их как некие точки с определённым положением на линии. Положение может быть отрицательным (-1), либо между другими числами (2²), либо в другом измерении (i).

Таким образом арифметика предстаёт перед нами как способ преобразовывать число. Сложение становится перемещением (+3 — это перемещение на 3 единицы вправо); умножение становится масштабированием (*3 — это увеличить число в три раза).

А что же такое тогда степень числа?

Познакомьтесь с Экпандотроном™

Это Экспандотрон 3000. Он выглядит как достаточно потрёпанная микроволновка, но вместо подогрева пищи она занимается ростом чисел. Просто положите число внутрь и проделайте несколько простых операций.

Начните с 1
Установите желаемый показатель «Роста» за одну секунду (2х, 3х, 10,3х и т.д.)
Установите желаемый показатель «Времени» в секундах
Нажмите кнопку START

Вуаля! После звукового сигнала достаём наше новенькое готовое число. Например, мы хотим изменить 1 на 9. Что нам нужно сделать?

Поместите 1 в Экспандотрон
Установите «Рост» на 3х, а «Время» на 2 секунды
Нажмите кнопку START

Что мы видим? Мы видим, как число начинает преобразовываться: 1; 1,1; 1,2. По окончании первой секунды оно уже выглядит как 3 и продолжает меняться: 3,1; 3,5; 4,0; 6,0; 7,5. И по окончании второй секунды оно превратилось в 9.

В математическом представлении Экспандотрон (или показательная функция) делает для нас следующее:

Например, 3 2 = 9/1. Основанием является то количество раз, в которое нам нужно вырастить число (х3), а степенью — количество времени (2). Формула типа 2 n означает «Используйте свой Экспандотрон на мощности х2 в течение n секунд».

Работу Экспандотрона мы всегда начинаем с 1, чтобы посмотреть, как он меняет одну единицу. Если мы хотим посмотреть, что случится с 3 в Экспандотроне, мы просто масштабируем конечный результат. Например:

Начните с 1 и умножьте на двойку в третьей степени: 1*2 3 = 1 * 2 * 2 * 2 = 8

Начните с 3 и умножьте на двойку в третьей степени: 3*2 3 = 3 * 2 * 2 * 2 = 24

Каждый раз, когда вы видите простую степень, вы начинаете с 1.

Идём к пониманию масштабирующего множителя

При умножении мы можем просто указать конечный масштабирующий множитель. Хотите число в 8 раз больше? Умножаем на 8. Готово.

Степени более капризны в обращении. Вот как они работают:

Вы: Хочу вырастить вот это число.

Экспандотрон: Ок, давай его сюда.

Вы: И насколько большим оно станет?

Экспандотрон: Пффф, без понятия. Давай посмотрим.

Вы: Посмотрим? Я думал, ты зна.

Экспандотрон: Тихо! Оно растёт! Растёт!

Экспандотрон: Готово! Это шедевр!

Экспандотрон не прямолинеен. Вы смотрите на него, но не знаете, что он сделает. Что значит 3 10 ? Степень числа вместо простого масштабирования заставляет нас почувствовать всеми органами процесс роста.

Это может звучать раздражающе неопределённо, но знаете, что? Большинство явлений природы заканчиваются неизвестно чем!

Как думаете, бактерия действительно планирует делиться каждые 14 часов? Нет, она просто питается забытым вами в холодильнике хлебом и растёт так быстро, как только может. Чтобы предсказать поведение этой бактерии, мы можем лишь использовать значения темпа её роста и длительности роста — и только потом мы получим конечное значение.

Иными словами, степень числа — это такой способ сказать «Начинаем с таких условий, изменяем их и смотрим, к чему мы придём». Этим и занимается наш Экспандотрон.

Идём к пониманию дробных степеней

Может ли Экспандотрон помочь нам осознать степени ещё глубже? Ну, к примеру, что означает 2 1,5 ?

Очень легко запутаться, если мы думаем о двойке в полуторной степени привычным способом — как о многократном умножении. Но в Экспандотроне всё просто: 1,5 — это всего лишь проведённое в нём время.

2 1 — это одна секунда в машине (двукратный рост)
2 2 — это две секунды в машине (четырёхкратный рост)

2 1,5 означает 1,5 секунды в машине, значит, этот рост окажется где-то между двукратным и четырёхкратным.

Умножение степеней

Что если мы захотим прогнать два цикла роста один за другим? Ну, например, мы используем машину в течение 2 секунд, а потом ещё 3 секунды на той же мощности:

Представьте самую обычную микроволновку. Разве это не будет самый обычный цикл длительностью в 5 секунд? Будет. Здесь происходит то же самое — раз уже мощность (основание) остаётся одинаковой, мы просто складываем время:

Квадратные корни

Продолжим. Предположим, мы выбрали мощность а и устанавливаем рост в течение 3 секунд:

Неплохо. Как будет выглядеть рост в течение половины этого времени? Логично, что 1,5 секунды.

А если мы проделаем то же самое два раза?

частичный рост * частичный рост = полный рост

Смотрим на это уравнение и видим, что «частичный рост» — это квадратный корень из значения полного роста. А если мы разделим время на три части?

частичный рост * частичный рост * частичный рост = полный рост

А вот и кубический корень! Это даёт нам интуитивное понимание того, почему деление степеней даёт нам корни: мы разбиваем время на равные доли.

Отрицательные степени

А как быть с отрицательными степенями? Отрицательные степени для нас будут значить обратный отсчёт во времени. Если движение вперёд во времени приводит нас к росту, движение назад, скорее всего, выльется в уменьшение числа.

Это значит следующее: «Секунду назад у нас была половина от текущего количества (1/2 1 ). Любой график экспоненциального роста строится именно так.

Выберите точку на шкале времени, например, 3,5 секунды (2 3,5 = 11,3). Через секунду мы удвоим наше количество (2 4,5 = 22,5). А секунду назад у нас была всего лишь половина от текущего количества (2 2,5 = 5,65).

Приходим к нулевой степени

Теперь самое интересное: что означает 3 0 ? А всё очень просто. Мы устанавливаем нашу микроволновку на мощность х3 и используем её в течение. 0 секунд. Это значит, что мы её просто не запускаем!

Значит, масштабирующий множитель равен единице, значит, никаких изменений с нашим числом не происходит. Новое число будет равняться исходному числу, то есть (вы же помните, что исходное число у нас единица?) единице. Масштабирования не происходит.

Приходим к нулевому основанию

А что мы делаем с 0 x ? Что ж, наша мощность в этом случае будет х0, а значит, после секунды времени Экспандотрон превращает число в ноль. Раз мы уже аннулировали число, совершенно неважно, сколько времени оно пробудет в машине — оно так и останется нулём.

Приходим к нулевому основанию в нулевой степени

Вот он, великий и ужасный 0 0 . И снова нас спасает Экспандотрон.

0 в степени 0 означает рост х0 в течение 0 секунд. Хоть мы и планировали аннулировать число, мы так и не запустили машину. Новое число равно исходному числу (то есть в наш Экспандотрон мы положили единицу), масштабирующий множитель тоже равен единице.

Конечно, Экспандотрона на самом деле не существует (а жаль!). Конечно, числа на самом деле не выстраиваются в линейку — они всего лишь один из множества способов взглянуть на мир.

Что даёт нам Экспандотрон? Он помогает нам не запинаться о кажущиеся препятствия вроде 2 1,5 или 0 0 . Как только мы начинаем понимать основные принципы роста, постепенно мы начнём дружить и с формулой Эйлера.

По материалам очаровательной статьи на Better Explained.

Свойства степеней и действия с ними

Зачем нужны степени? Где они тебе пригодятся? Почему тебе нужно тратить время на их изучение?

Как обычно – чтобы облегчить себе жизнь. Знание свойств степеней позволит тебе упрощать вычисления и считать быстрее, что пригодится и в жизни и на ОГЭ или ЕГЭ!

Чтобы узнать все о степенях и научиться пользоваться свойствами степеней, читай эту статью.

P.S Если ты хорошо знаешь степени и тебе надо только повторить, переходи сразу к продвинутому уровню.

НАЧАЛЬНЫЙ УРОВЕНЬ

Степени. Коротко о главном

Определение степени:

Свойства степеней:

Произведение степеней с одинаковым основанием:	( <^>cdot <^>=<^>)
Произведение степеней с одинаковыми показателями:	( <^>cdot <^>=<^>)
Деление степеней с одинаковым основанием:	( frac<<^>><<^>>=<^>)
Деление степеней с одинаковыми показателями:	( frac<<^>><<^>>=<right)>^>)
Возведение степени в степень:	( <> right)>^>=<^>)
Дробная степень:	( <^>>=sqrt[m]<<^>>)

Особенности степеней:

Отрицательное число, возведенное в четную степень, – число положительное;
Отрицательное число, возведенное в нечетную степень, – число отрицательное;
Положительное число в любой степени – число положительное;
Ноль в любой степени равен ( 0);
Любое число в нулевой степени равно ( 1);
Степень с целым показателем – это степень, показатель которой натуральное число (т.е. целое и положительное);
Степень с рациональным показателем – это степень, показатель которой отрицательные и дробные числа;
Степень с иррациональным показателем – это степень, показатель которой бесконечная десятичная дробь или корень.

Возведение в степень – это такая же математическая операция, как сложение, вычитание, умножение или деление.

Сейчас объясню все человеческим языком на очень простых примерах. Будь внимателен. Примеры элементарные, но объясняющий важные вещи. Начнем со сложения.

Сложение

Объяснять тут нечего. Ты и так все знаешь: нас восемь человек. У каждого по две бутылки колы. Сколько всего колы? Правильно – 16 бутылок. Теперь умножение.

Умножение

Тот же самый пример с колой можно записать по-другому: (displaystyle 2cdot 8=16).

Математики – люди хитрые и ленивые. Они сначала замечают какие-то закономерности, а потом придумывают способ как быстрее их «считать».

В нашем случае они заметили, что у каждого из восьми человек одинаковое количество бутылок колы и придумали прием, который называется умножением.

Согласись, (displaystyle 2cdot 8=16) считается легче и быстрее, чем (displaystyle 2+2+2+2+2+2+2+2=16).

И еще одна важная деталь. Ошибок при таком счете делается гораздо меньше. Математики из Стэнфорда, кстати, считают, что человек, знающий приемы счета, делает это в два раза легче и быстрее и совершает в два раза меньше ошибок. Работы меньше, а результат лучше.

Итак, чтобы считать быстрее, легче и без ошибок, нужно всего лишь запомнить таблицу умножения. Ты, конечно, можешь делать все медленнее, труднее и с ошибками, но лучше ее запомнить! Вот таблица умножения. Выучи ее наизусть.

И другая таблица, красивее:

А какие еще хитрые приемы счета придумали ленивые математики? Правильно – возведение числа в степень.

Возведение числа в степень

Если тебе нужно умножить число само на себя пять раз, то математики говорят, что тебе нужно возвести это число в пятую степень.

Например, (displaystyle 2cdot 2cdot 2cdot 2cdot 2=<<2>^<5>>). Математики помнят, что два в пятой степени – это (displaystyle 32).

И решают такие задачки в уме – быстрее, легче и без ошибок.

Для этого нужно всего лишь запомнить то, что выделено цветом в таблице степеней чисел. Поверь, это сильно облегчит тебе жизнь.

Кстати, почему вторую степень называют квадратом числа, а третью – кубом? Что это значит? Очень хороший вопрос. Сейчас будут тебе и квадраты, и кубы.

Примеры из жизни

Начнем с квадрата или со второй степени числа.

Представь себе квадратный бассейн размером ( displaystyle 3) метра на ( displaystyle 3) метра. Бассейн стоит у тебя на даче. Жара и очень хочется купаться.

Но… бассейн без дна! Нужно застелить дно бассейна плиткой. Сколько тебе надо плитки? Для того чтобы это определить, тебе нужно узнать площадь дна бассейна.

Ты можешь просто посчитать, тыкая пальцем, что дно бассейна состоит из ( displaystyle 9) кубиков метр на метр. Если у тебя плитка метр на метр, тебе нужно будет ( displaystyle 9) кусков. Это легко…

Но где ты видел такую плитку? Плитка скорее будет ( displaystyle 10) см на ( displaystyle 10) см. И тогда «пальцем считать» замучаешься. Тогда придется умножать.

Итак, по одной стороне дна бассейна у нас поместится ( displaystyle 30) плиток (( displaystyle frac<300 см><10 см>=30) штук) и по другой тоже ( displaystyle 30) плиток.

Умножив ( displaystyle 30) на ( displaystyle 30) , ты получишь ( displaystyle 900) плиток (( displaystyle 30cdot 30=900) ).

Ты заметил, что для определения площади дна бассейна мы умножили одно и то же число само на себя? Что это значит? Раз умножается одно и то же число, мы можем воспользоваться приемом «возведение в степень».

Конечно, когда у тебя всего два числа, все равно перемножить их или возвести в степень. Но если у тебя их много, то возводить в степень значительно проще и ошибок при расчетах получается тоже меньше.

Итак, тридцать во второй степени будет ( displaystyle 900) (( displaystyle <<30>^<2>>=900) ). Или же можно сказать, что тридцать в квадрате будет ( displaystyle 900) .

Иными словами, вторую степень числа всегда можно представить в виде квадрата. И наоборот, если ты видишь квадрат – это ВСЕГДА вторая степень какого-то числа.

Квадрат – это изображение второй степени числа.

Вот тебе задание, посчитать, сумму белых и черных квадратов на шахматной доске с помощью квадрата числа… По одной стороне ( displaystyle клеток и по другой тоже ( displaystyle .

Чтобы посчитать их количество, нужно восемь умножить на восемь или… если заметить, что шахматная доска – это квадрат со стороной ( displaystyle , то можно возвести восемь в квадрат. Получится ( displaystyle 64) клетки (( displaystyle 8cdot 8=<<8>^<2>>=64)). Так?

Теперь куб или третья степень числа. Тот же самый бассейн. Но теперь тебе нужно узнать, сколько воды придется залить в этот бассейн. Тебе нужно посчитать объем. (Объемы и жидкости, кстати, измеряются в кубических метрах. Неожиданно, правда?)

Нарисуй бассейн: дно размером ( displaystyle 3) на ( displaystyle 3) метра и глубиной ( displaystyle 3) метра и попробуй посчитать, сколько всего кубов размером метр на метр войдет в твой бассейн.

Прямо показывай пальцем и считай! Раз, два, три, четыре…двадцать два, двадцать три… Сколько получилось? Не сбился? Трудно пальцем считать?

Так-то! Бери пример с математиков. Они ленивы, поэтому заметили, что чтобы посчитать объем бассейна, надо перемножить друг на друга его длину, ширину и высоту.

В нашем случае объем бассейна будет равен ( displaystyle 3cdot 3cdot 3=27) кубов… Легче правда?

А теперь представь, насколько математики ленивы и хитры, если они и это упростили. Свели все к одному действию. Они заметили, что длина, ширина и высота равна и что одно и то же число перемножается само на себя…

А что это значит? Это значит, что можно воспользоваться степенью. Итак, то, что ты ( displaystyle 27) раз считал пальцем, они делают в одно действие: три в кубе равно ( displaystyle 27) . Записывается это так: ( displaystyle <<3>^<3>>=27) .

Остается только запомнить таблицу степеней. Если ты, конечно, такой же ленивый и хитрый как математики. Если любишь много работать и делать ошибки – можешь продолжать считать пальцем.

Ну и чтобы окончательно убедить тебя, что степени придумали лодыри и хитрюги для решения своих жизненных проблем, а не для того чтобы создать тебе проблемы, вот тебе еще пара примеров из жизни.

У тебя есть ( displaystyle 2) миллиона рублей. В начале каждого года ты зарабатываешь на каждом миллионе еще один миллион. То есть каждый твой миллион в начале каждого года удваивается. Сколько денег у тебя будет через ( displaystyle 5) лет?

Если ты сейчас сидишь и «считаешь пальцем», значит ты очень трудолюбивый человек и.. глупый. Но скорее всего ты дашь ответ через пару секунд, потому что ты – умный! Итак, в первый год – два умножить на два… во второй год – то, что получилось, еще на два, в третий год… Стоп!

Ты заметил, что число ( displaystyle 2) перемножается само на себя ( displaystyle 6) раз. Значит, два в шестой степени – ( displaystyle 64) миллиона! А теперь представь, что у вас соревнование и эти ( displaystyle 64) миллиона получит тот, кто быстрее посчитает…

Стоит запомнить степени чисел, как считаешь?

У тебя есть ( displaystyle 1) миллион. В начале каждого года ты зарабатываешь на каждом миллионе еще два. Здорово правда? Каждый миллион утраивается. Сколько денег у тебя будет через ( displaystyle 4) года?

Давай считать. Первый год – ( displaystyle 1) умножить на ( displaystyle 3) , потом результат еще на ( displaystyle 3) …

Уже скучно, потому что ты уже все понял: три умножается само на себя ( displaystyle 4) раза.

Значит ( displaystyle 3) в четвертой степени равно ( displaystyle 81) миллион. Надо просто помнить, что три в четвертой степени это ( displaystyle 81) или ( displaystyle <<3>^<4>>=81) .

Теперь ты знаешь, что с помощью возведения числа в степень ты здорово облегчишь себе жизнь. Давай дальше посмотрим на то, что можно делать со степенями и что тебе нужно знать о них.

Что такое степень числа

Обращаем ваше внимание, что в данном разделе разбирается понятие степени только с натуральным показателем и нулём.

Понятие и свойства степеней с рациональными показателями (с отрицательным и дробным) будут рассмотрены в уроках для 8 класса.

Итак, разберёмся, что такое степень числа. Для записи произведения числа самого на себя несколько раз применяют сокращённое обозначение.

Вместо произведения шести одинаковых множителей 4 · 4 · 4 · 4 · 4 · 4 пишут 4 6 и произносят «четыре в шестой степени».

4 · 4 · 4 · 4 · 4 · 4 = 4 6

Выражение 4 6 называют степенью числа, где:

4 — основание степени;
6 — показатель степени.

В общем виде степень с основанием « a » и показателем « n » записывается с помощью выражения:

Степенью числа « a » с натуральным показателем « n », бóльшим 1 , называется произведение « n » одинаковых множителей, каждый из которых равен числу « a ».

Запись « a n » читается так: « а в степени n » или « n -ая степень числа a ».

Исключение составляют записи:

a 2 — её можно произносить как « а в квадрате»;
a 3 — её можно произносить как « а в кубе».

Конечно, выражения выше можно читать и по определению степени:

a 2 — « а во второй степени»;
a 3 — « а в третьей степени».

Особые случаи возникают, если показатель степени равен единице или нулю (n = 1; n = 0) .

Степенью числа « а » с показателем n = 1 является само это число:
a 1 = a

Любое число в нулевой степени равно единице.
a 0 = 1

Ноль в любой натуральной степени равен нулю.
0 n = 0

Единица в любой степени равна 1.
1 n = 1

Выражение 0 0 (ноль в нулевой степени) считают лишённым смысла.

(−32) 0 = 1
0 253 = 0
1 4 = 1

При решении примеров нужно помнить, что возведением в степень называется нахождение числового или буквенного значения после его возведения в степень.

Пример. Возвести в степень.

5 3 = 5 · 5 · 5 = 125
2,5 2 = 2,5 · 2,5 = 6,25
(

3
4

) 4 =

3
4

·

3
4

·

3
4

·

3
4

=

3 · 3 · 3 · 3
4 · 4 · 4 · 4

=

81
256

Возведение в степень отрицательного числа

Основание степени (число, которое возводят в степень) может быть любым числом — положительным, отрицательным или нулём.

При возведении в степень положительного числа получается положительное число.

При возведении нуля в натуральную степень получается ноль.

При возведении в степень отрицательного числа в результате может получиться как положительное число, так и отрицательное число. Это зависит от того чётным или нечётным числом был показатель степени.

Рассмотрим примеры возведения в степень отрицательных чисел.

Из рассмотренных примеров видно, что если отрицательное число возводится в нечётную степень, то получается отрицательное число. Так как произведение нечётного количество отрицательных сомножителей отрицательно.

Если же отрицательное число возводится в чётную степень, то получается положительное число. Так как произведение чётного количество отрицательных сомножителей положительно.

Отрицательное число, возведённое в чётную степень, есть число положительное .

Отрицательное число, возведённое в нечётную степень, — число отрицательное .

Квадрат любого числа есть положительное число или нуль, то есть:

a 2 ≥ 0 при любом a .

2 · (−3) 2 = 2 · (−3) · (−3) = 2 · 9 = 18
−5 · (−2) 3 = −5 · (−8) = 40

Обратите внимание!

При решении примеров на возведение в степень часто делают ошибки, забывая, что записи (−5) 4 и −5 4 это разные выражения. Результаты возведения в степень данных выражений будут разные.

Вычислить (−5) 4 означает найти значение четвёртой степени отрицательного числа.

В то время как найти « −5 4 » означает, что пример нужно решать в 2 действия:

Возвести в четвёртую степень положительное число 5 .
5 4 = 5 · 5 · 5 · 5 = 625
Поставить перед полученным результатом знак «минус» (то есть выполнить действие вычитание).
−5 4 = −625

Пример. Вычислить: −6 2 − (−1) 4

6 2 = 6 · 6 = 36
−6 2 = −36
(−1) 4 = (−1) · (−1) · (−1) · (−1) = 1
−(−1) 4 = −1
−36 − 1 = −37

Порядок действий в примерах со степенями

Вычисление значения называется действием возведения в степень. Это действие третьей ступени.

В выражениях со степенями, не содержащими скобки, сначала выполняют вовзведение в степень, затем умножение и деление , а в конце сложение и вычитание .

Если в выражении есть скобки, то сначала в указанном выше порядке выполняют действия в скобках, а потом оставшиеся действия в том же порядке слева направо.