Внутренние односторонние углы — теория, правило и свойства
Чтобы дать верное определение внутренним односторонним углам, нужно отличать их от вертикальных, смежных, соответственных и накрест лежащих. Их объединяет то, что они могут быть образованы двумя параллельными прямыми и пересекающей их линией. Утверждение о том, что сумма внутренних односторонних углов составляет 180 градусов, позволяет доказать теорему о параллельности прямых.

Углы по определению
Прямая, которая пересекает другие линии, идущие параллельно друг другу, образует не только внутренние, но и внешние углы. Один из них дополняет другой до 180 градусов. Это свойство можно доказать как для смежных, так и односторонних внутренних, каждый из которых имеет соответственный внешний.
Углы, расположенные на одной стороне от секущей, пересекающей 2 линии, идущие параллельно, называются накрест лежащими. Они отличаются от односторонних, образуя с ними смежные. В сумме они составляют 180 градусов.
Отрезок между линиями, проведенными параллельно между собой, можно обозначить AB. Если представить, что AB=0, то параллельные будут совпадать, а соответственные углы и односторонние станут смежными. Их сумма должна быть 180 градусов.
Доказательство теоремы
Прямые являются параллельными, если сумма односторонних внутренних углов равна 180. Нужно доказать теорему по исходным данным. Секущая АВ является линией пересечения параллельных а и b.
Для доказательства теоремы можно допустить, что линии не являются параллельными, значит они пересекают друг друга в определенной точке С. Секущая АВ образует с а и b треугольник АВС, поскольку точка С лежит в одной из двух плоскостей относительно АВ. На линии а расположена сторона треугольника АС, а на b — ВС.

Если в противоположной полуплоскости отложить точку С1, то она образует с АВ другой треугольник АВС1. При этом по построению углы ВАС и АВС1 равны. Сумма САВ и СВА составляет 180, что указано в условии задачи. Следовательно, сторона АС1 принадлежит а, аналогично, ВС1 — линии b.
Точка пересечения С линий а и b принадлежит этим прямым. Вместе с тем точка С1 не может лежать на каждой из них, поскольку она находится в полуплоскости, где линии по построению не пересекаются.
Если в сумме односторонние углы составляют 180, то треугольника АВС1 не существует, значит а || b.
Следствие из свойства прямых
На прямую а может быть опущен единственный перпендикуляр из любой точки А, которая не принадлежит данной линии. Доказательство утверждения состоит из следующих шагов:

Итак, отрезок АВ является единственным перпендикуляром, проходящим через точку А.
Построение параллелограмма
Если односторонние углы не прямые, то один из них является острым, а другой — тупым, то есть меньшим или большим по величине. Если через каждый из них провести биссектрисы, то они должны пересечь противоположные стороны в определенных точках. Для этого достаточно отложить отрезки на параллельных линиях, равные AB, используя циркуль.

Секущая и отрезки, принадлежащие проведенным биссектрисам, образуют 2 треугольника вместе с параллельными. Напротив большего угла будет находиться биссектриса, отсекающая наибольший отрезок. Это подтверждает теорема о соотношении между углами и сторонами разностороннего треугольника.
Соединив точки пересечения биссектрис с параллельными прямыми, можно построить четырехугольник ABCD. Чтобы доказать, что полученная фигура является параллелограммом, достаточно учесть следующее:
Отложив от A и B равноудаленные точки C и D, можно получить линию CD, которая параллельна AB. Тогда CD — отрезок, перпендикулярный параллельным прямым BC и AD. Поскольку все отрезки полученной фигуры ABCD пересекаются перпендикулярно, то она является прямоугольником по построению.
Доказательство теоремы позволяет определять, какой является величина второго из двух внутренних односторонних углов при параллельных прямых и секущей. Решение задач по геометрии позволяет найти их градусную меру и в зависимости от разности между ними.
Геометрия. Урок 2. Углы
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Углы
Понятие угла
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Стороны угла – лучи, которые образуют угол.
Вершина угла – точка, из которой выходят лучи.

Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.
Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠ A O B или ∠ B O A , но ни в коем случае не ∠ O A B , ∠ O B A , ∠ A B O , ∠ B A O .
Величину угла измеряют в градусах. ∠ A O B = 24 ° .
Виды углов:
Биссектриса угла
Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.
Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.
O D – биссектриса угла ∠ A O B . Она делит этот угол на два равных угла.
∠ A O D = ∠ B O D = ∠ A O B 2
Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон O A и O B угла ∠ A O B .
Углы, образованные при пересечении двух прямых
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.
Свойство: сумма смежных углов равна 180 ° .
( 1 ) и ( 3 )
( 2 ) и ( 4 )
называются вертикальными .
По свойству вертикальных углов:
∠ C O D = ∠ A O B
∠ B O D = ∠ A O C
( 1 ) и ( 2 )
( 2 ) и ( 3 )
( 3 ) и ( 4 )
( 4 ) и ( 1 )
называются смежными .
По свойству смежных углов:
∠ C O D + ∠ D O B = 180 ° ∠ D O B + ∠ B O A = 180 ° ∠ B O A + ∠ A O C = 180 ° ∠ A O C + ∠ C O D = 180 °
Углы, образованные при пересечении двух прямых секущей
Прямая, пересекающая две заданные прямые, называется секущей этих прямых.
Существует пять видов углов, которые образуются при пересечении двух прямых секущей.
( 1 ) и ( 5 )
( 2 ) и ( 6 )
( 3 ) и ( 7 )
( 4 ) и ( 8 )
называются соответственными .
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).
( 3 ) и ( 5 )
( 4 ) и ( 6 )
называются внутренними односторонними .
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).
( 1 ) и ( 7 )
( 2 ) и ( 8 )
называются внешними односторонними .
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).
( 3 ) и ( 6 )
( 4 ) и ( 5 )
называются внутренними накрест лежащими .
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).
( 1 ) и ( 8 )
( 2 ) и ( 7 )
называются внешними накрест лежащими .
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).
Если прямые, которые пересекает секущая, параллельны , то углы имеют следующие свойства:
- Соответственные углы равны.
- Внутренние накрест лежащие углы равны.
- Внешние накрест лежащие углы равны.
- Сумма внутренних односторонних углов равна 180 ° .
- Сумма внешних односторонних углов равна 180 ° .
Сумма углов многоугольника
Сумма углов произвольного n -угольника вычисляется по формуле:
S n = 180 ° ⋅ ( n − 2 )
где n – это количество углов в n -угольнике.
Пользуясь этой формулой, можно вычислить сумму углов для произвольного n -угольника.
Сумма углов треугольника: S 3 = 180 ° ⋅ ( 3 − 2 ) = 180 °
Сумма углов четырехугольника: S 4 = 180 ° ⋅ ( 4 − 2 ) = 360 °
Сумма углов пятиугольника: S 5 = 180 ° ⋅ ( 5 − 2 ) = 540 °
Так можно продолжать до бесконечности.
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.
На рисунках изображены примеры правильных многоугольников:



Чтобы найти величину угла правильного n -угольника , необходимо сумму углов этого многоугольника разделить на количество углов.
α n = 180 ° ⋅ ( n − 2 ) n
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с углами
Признаки параллельности прямых
При пересечении двух прямых третьей прямой образуются углы, названия которых приведены в следующей таблице.
Углы, образующиеся при пересечении двух прямых третьей прямой
| Рисунок | Определение углов |
 |
Внутренние накрест лежащие углы |
 |
|
 |
Внешние накрест лежащие углы |
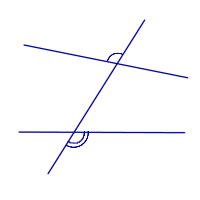 |
|
 |
Соответственные углы |
 |
|
 |
|
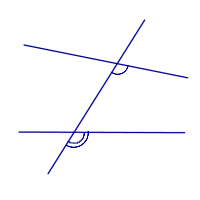 |
|
 |
Внутренние односторонние углы |
 |
|
 |
Внешние односторонние углы |
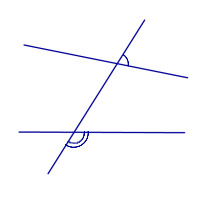 |
| Внутренние накрест лежащие углы |
 |
 |
| Внешние накрест лежащие углы |
 |
 |
| Соответственные углы |
 |
 |
 |
 |
| Внутренние односторонние углы |
 |
 |
| Внешние односторонние углы |
 |
 |
Перечисленные в таблице углы используются в формулировках признаков параллельности двух прямых.
Определение . Две прямые на плоскости называются параллельными, если они не имеют общих точек.
Замечание . Два отрезка называются параллельными , если они лежат на параллельных прямых.
Признаки параллельности двух прямых
| Рисунок | Признак параллельности |
 |
Прямые параллельны тогда и только тогда, когда внутренние накрест лежащие углы равны |
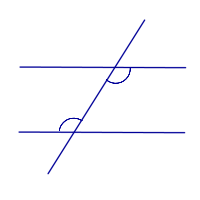 |
|
 |
Прямые параллельны тогда и только тогда, когда внешние накрест лежащие углы равны |
 |
|
 |
Прямые параллельны тогда и только тогда, когда соответственные углы равны |
 |
|
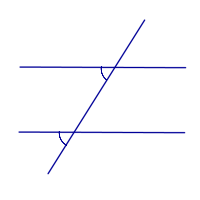 |
|
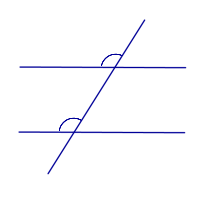 |
|
 |
Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180° |
 |
|
 |
Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180° |
 |
Прямые параллельны тогда и только тогда,
когда внутренние накрест лежащие углы равны

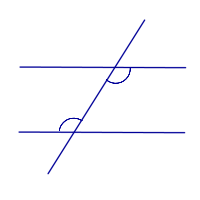
Прямые параллельны тогда и только тогда,
когда внешние накрест лежащие углы равны


Прямые параллельны тогда и только тогда,
когда соответственные углы равны


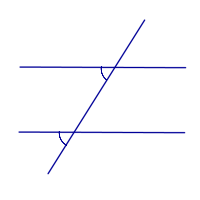
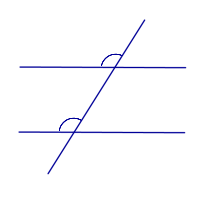
Прямые параллельны тогда и только тогда, когда сумма внутренних односторонних углов равна 180°


Прямые параллельны тогда и только тогда, когда сумма внешних односторонних углов равна 180°


| Рисунок | Признак параллельности |
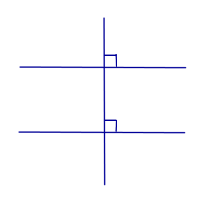 |
Две прямые, перпендикулярные к третьей прямой, параллельны |
Две прямые, перпендикулярные к третьей прямой, параллельны

Переход свойства параллельности прямых
| Рисунок | Признак параллельности |
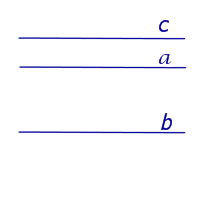 |
Если прямая a параллельна прямой b , а прямая b параллельна прямой c , то прямая a параллельна прямой c |
Если прямая a параллельна прямой b ,
а прямая b параллельна прямой c ,
то прямая a параллельна прямой c

Задача . Доказать, что биссектрисы внутренних односторонних углов, полученных при пересечении двух параллельных прямых третьей прямой, перпендикулярны.
Решение . Решение этой задачи почти дословно совпадает с решением задачи из раздела нашего справочника «Углы на плоскости» и предоставляется читателю в качестве несложного самостоятельного упражнения.
Геометрическая фигура угол: определение угла, измерение углов, обозначения и примеры
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
Дана прямая a на плоскости. На ней обозначим некоторую точку O . Прямая разделена точкой на две части, каждая из которых имеет название луч, а точка O – начало луча.
Иначе говоря, луч или полупрямая – это часть прямой, состоящая из точек заданной прямой, расположенных на одной стороне относительно начальной точки, то есть точки O .

Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
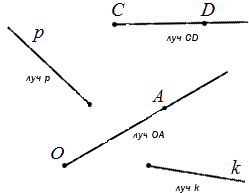
Перейдем к понятию определения угла.
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
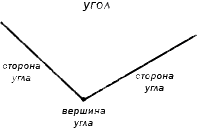
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.

Точка на прямой – это и есть вершина угла. Чаще всего имеет место ее обозначение точкой O .
Угол в математике обозначается знаком « ∠ ». Когда стороны угла обозначают малыми латинскими, то для правильного определения угла записываются подряд буквы соответственно сторонам. Если две стороны имеют обозначение k и h , то угол обозначается как ∠ k h или ∠ h k .
Когда идет обозначение большими буквами, то соответственно стороны угла имеют названия O A и O B . В таком случае угол имеет название из трех букв латинского алфавита, записанные подряд, в центре с вершиной – ∠ A O B и ∠ B O A . Существует обозначение в виде цифр, когда углы не имеют названий или буквенных обозначений. Ниже приведен рисунок, где разными способами обозначаются углы.
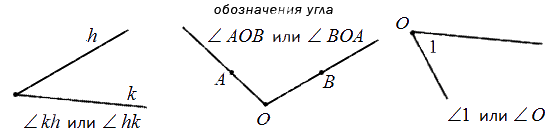
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
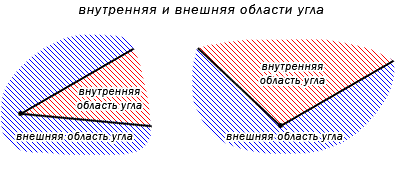
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
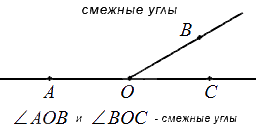
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
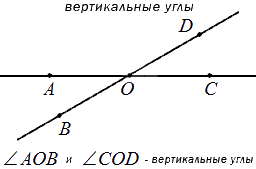
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
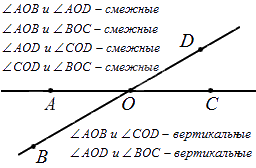
Сравнение углов
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
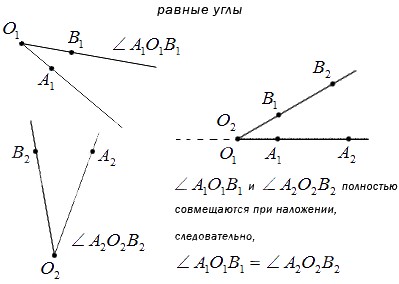
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
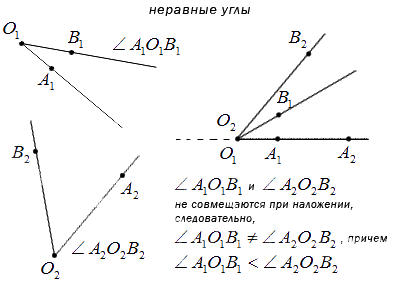
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Стандартное обозначение градуса идет при помощи « ° », тогда один градус – 1 ° . Следовательно, развернутый угол состоит из 180 таких углов, состоящих из одного градуса. Все имеющиеся углы плотно уложены друг к другу и стороны предыдущего совмещены с последующим.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
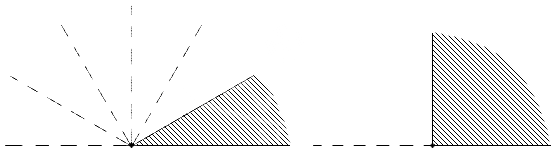
Для точности определения измерения углов используются минуты и секунды. Их применяют, когда величина угла не является целым обозначением градуса. Такие части градуса позволяют выполнять более точные расчеты .
Минутой называют одну шестидесятую часть градуса.
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « ‘ », а секунды « ” ». Имеет место обозначение:
1 ° = 60 ‘ = 3600 ” , 1 ‘ = ( 1 60 ) ° , 1 ‘ = 60 ” , 1 ” = ( 1 60 ) ‘ = ( 1 3600 ) ° ,
а обозначение угла 17 градусов 3 минут и 59 секунд имеет вид 17 ° 3 ‘ 59 ” .
Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Приведем пример обозначения градусной меры угла равного 17 ° 3 ‘ 59 ” . Запись имеет еще один вид 17 + 3 60 + 59 3600 = 17 239 3600 .
Для точного измерения углов используют такой измерительный прибор, как транспортир. При обозначении угла ∠ A O B и его градусной мере в 110 градусов применяют более удобную запись ∠ A O B = 110 ° , которая читается «Угол А О В равен 110 градусам».
В геометрии используется мера угла из интервала ( 0 , 180 ] , а в тригонометрии произвольная градусная мера имеет название углов поворота. Значение углов всегда выражается действительным числом. Прямой угол – это угол, имеющий 90 градусов. Острый угол – угол, который меньше 90 градусов, а тупой – больше.
Острый угол измеряется в интервале ( 0 , 90 ) , а тупой – ( 90 , 180 ) . Ниже наглядно изображены три вида углов.
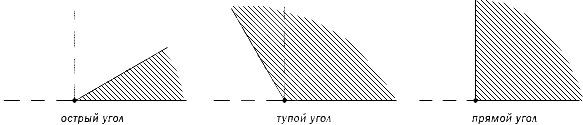
Любая градусная мера любого угла имеет одинаковое значение. Больший угол соответственно имеет большую градусную меру, чем меньший. Градусная мера одного угла – это сумма всех имеющихся градусных мер внутренних углов. Ниже приведен рисунок, где показан угол АОВ, состоящий из углов АОС, СОD и DОВ. Подробно это выглядит так: ∠ A O B = ∠ A O C + ∠ D O B = 45 ° + 30 ° + 60 ° = 135 ° .
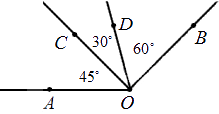
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Отсюда следует, что любые вертикальные углы равны. Если рассмотреть это на примере, мы получим, что угол А О В и С О D – вертикальные (на чертеже), тогда пары углов А О В и В О С , С О D и В О С считают смежными. В таком случает равенство ∠ A O B + ∠ B O C = 180 ° вместе с ∠ C O D + ∠ B O C = 180 ° считаются однозначно верными. Отсюда имеем, что ∠ A O B = ∠ C O D . Ниже приводится пример изображения и обозначения вертикальных улов.
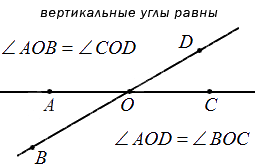
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
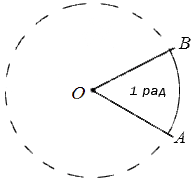
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
На рисунке радиан изображается в виде окружности, где имеется центр, обозначенный точкой , с двумя точками на окружности, соединенными и преобразованными в радиусы О А и О В . По определению данный треугольник A O B является равносторонним, значит длина дуги A B равна длинам радиусов О В и О А .
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
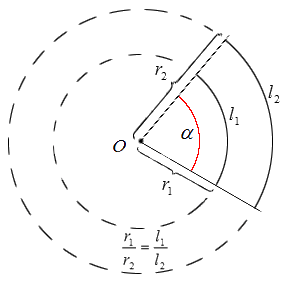
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
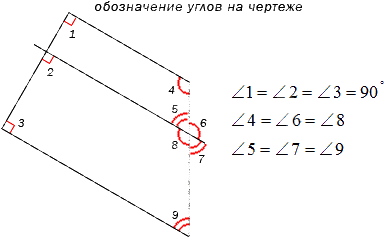
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
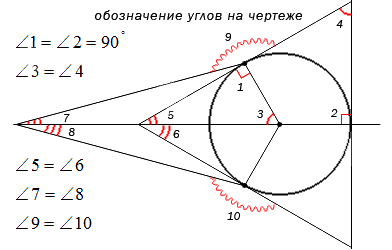
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Что такое угол? Виды углов

О чем эта статья:
2 класс, 5 класс
Определение угла
Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.
Если нам дана прямая a на плоскости, и на ней есть некоторая точку O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.
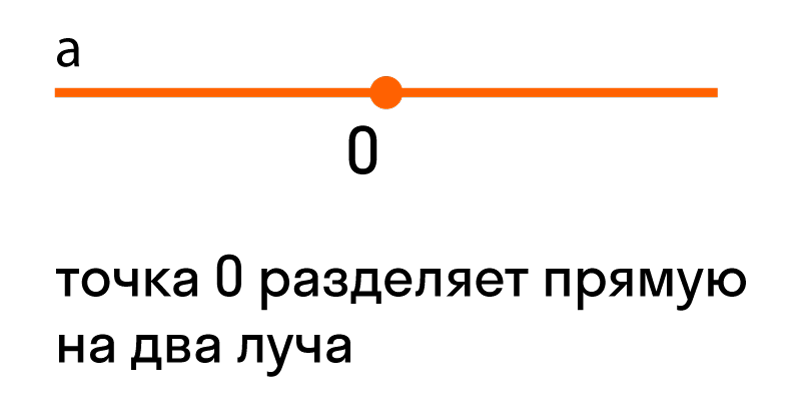
Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:
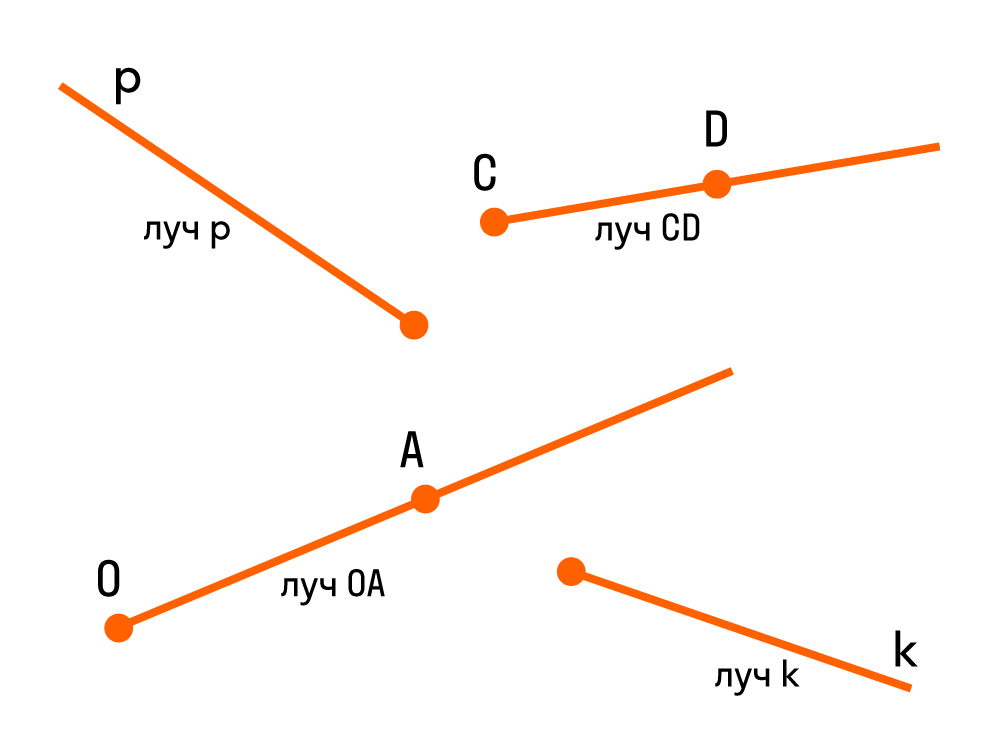
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.
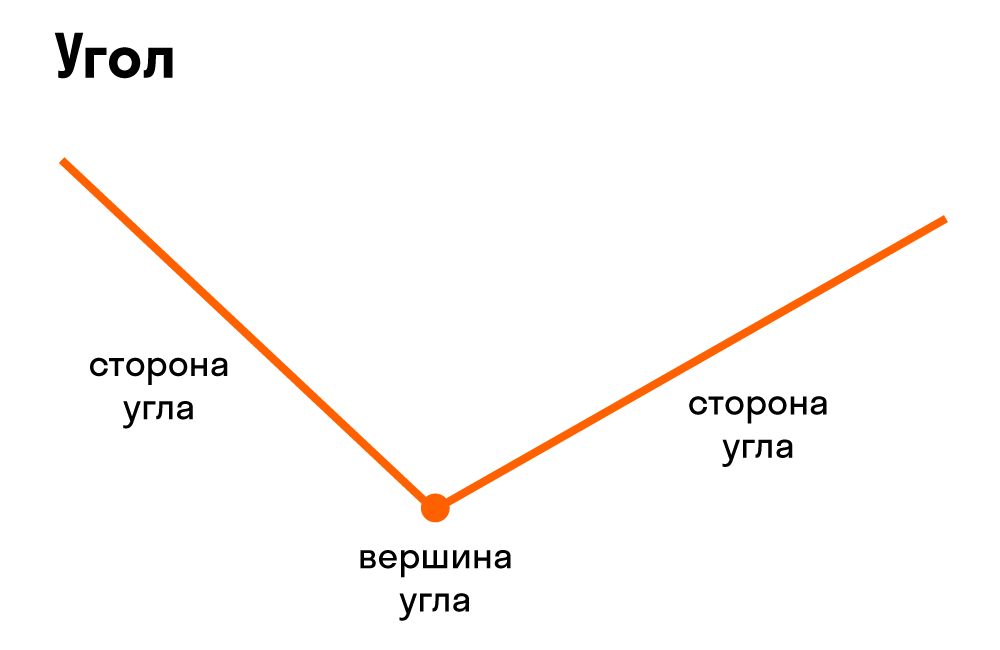
В математике существует специальный символ для обозначения угла, вот он: ∠.
Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.
Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA.
Иногда можно встретить обозначение в виде цифр — так тоже можно.
Для наглядности — все способы обозначения углов:
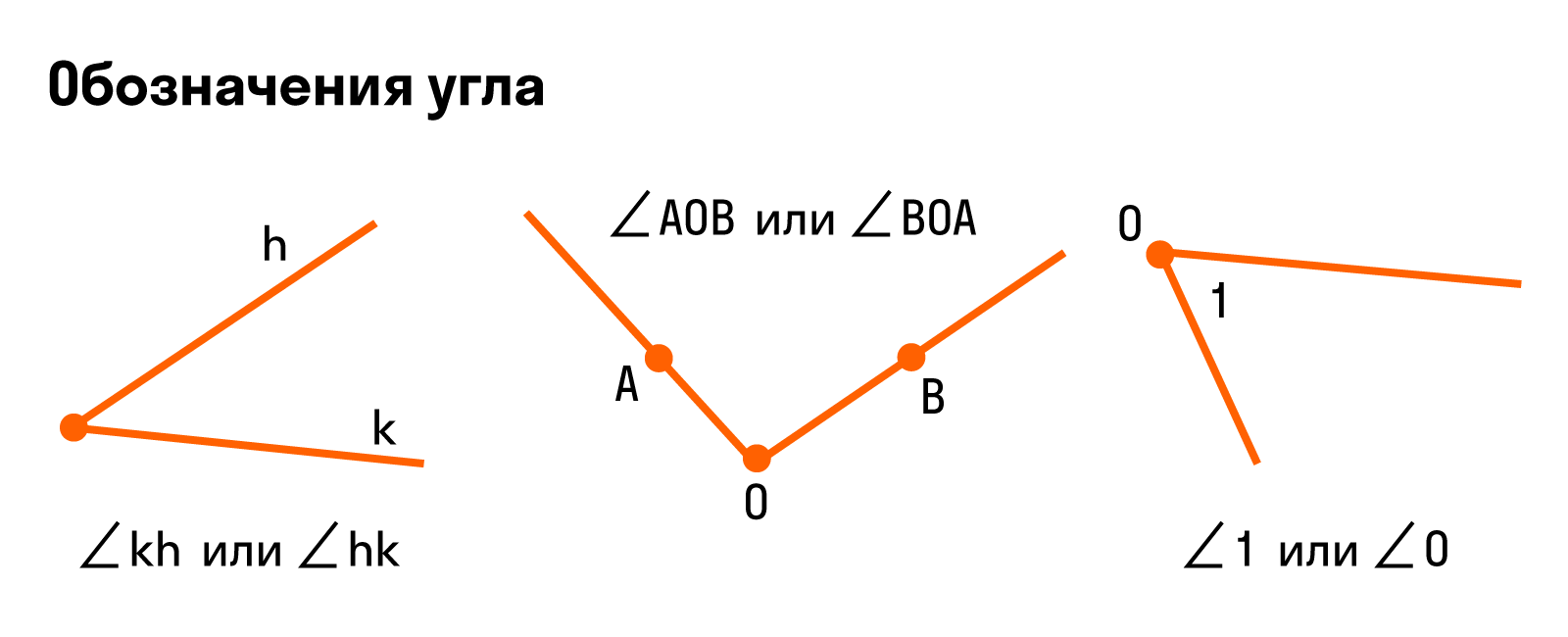
Что такое вершина и стороны угла:
- Стороны угла — лучи, из которых состоит угол.
- Вершина угла — общее начало сторон угла.
Биссектриса — это луч, который исходит из вершины угла и делит его на два равных угла.
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:
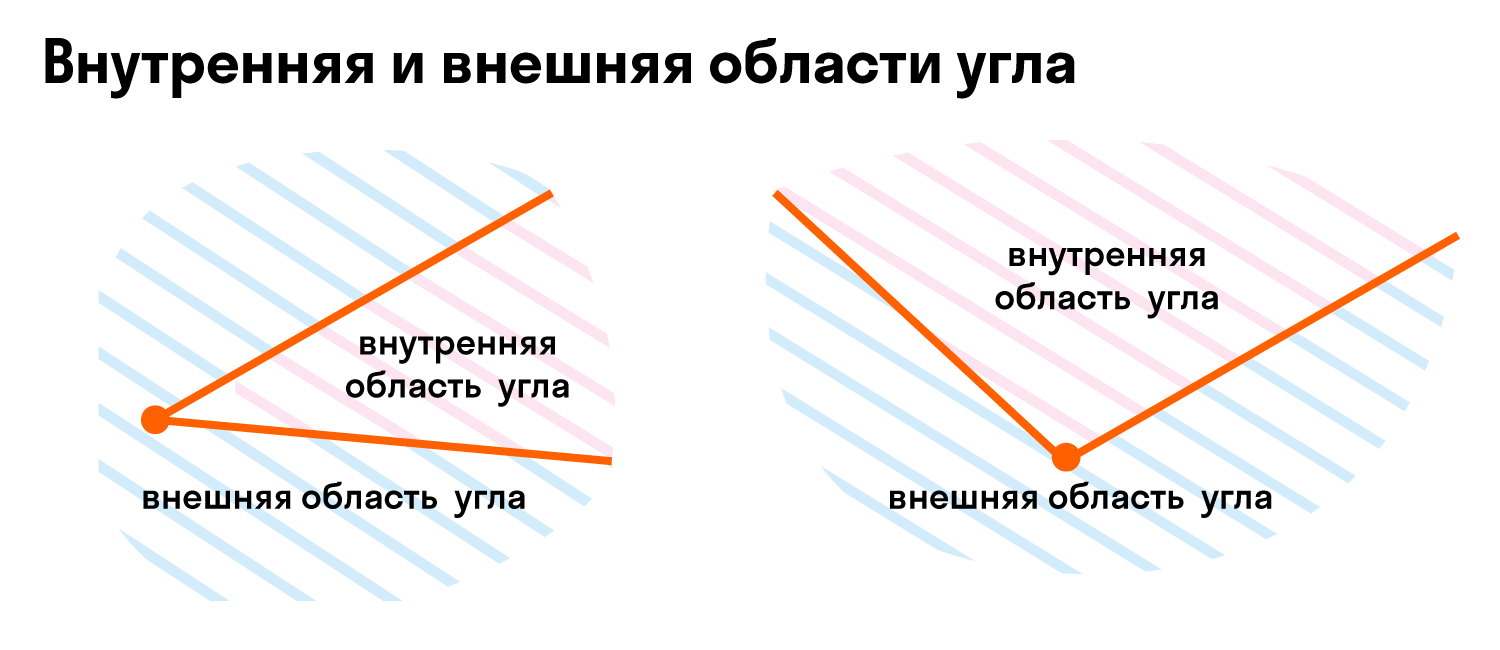
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Единица измерения углов — градусы. Символ для обозначения градуса угла: °.
Определение смежных и вертикальных углов
Смежные углы — это пара углов, у которых одна сторона общая, а две другие стороны лежат на одной прямой. Таким образом два смежных угла составляют развернутый угол. Общая сторона двух смежных углов называется наклонной к прямой, на которой лежат другие стороны, при условии, что смежные углы не равны.
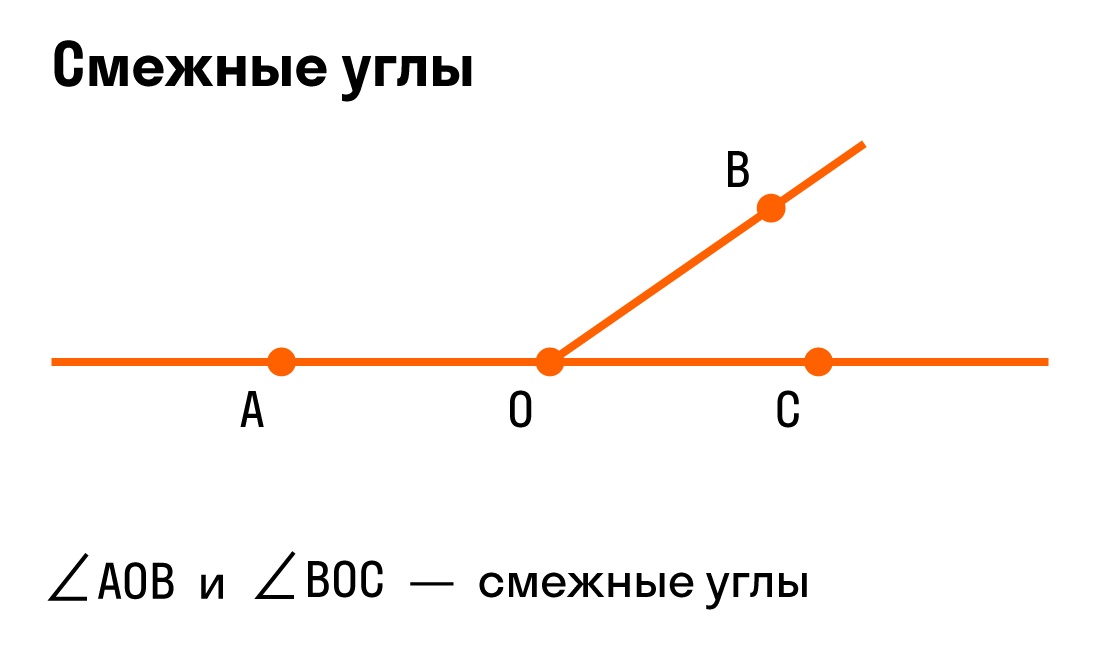
Вертикальные углы — это пара углов, у которых есть общая вершина, при этом стороны одного угла составляют продолжение сторон другого угла.
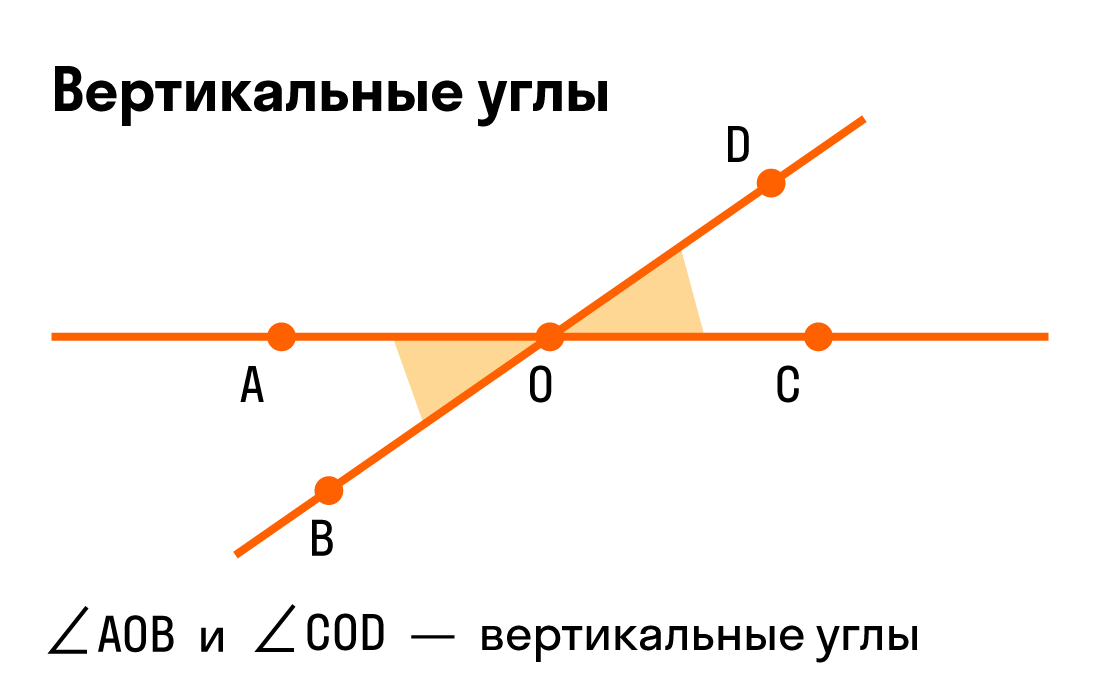
При пересечении прямых получается четыре пары смежных и две пары вертикальных углов. Вот как это выглядит:
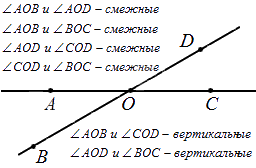
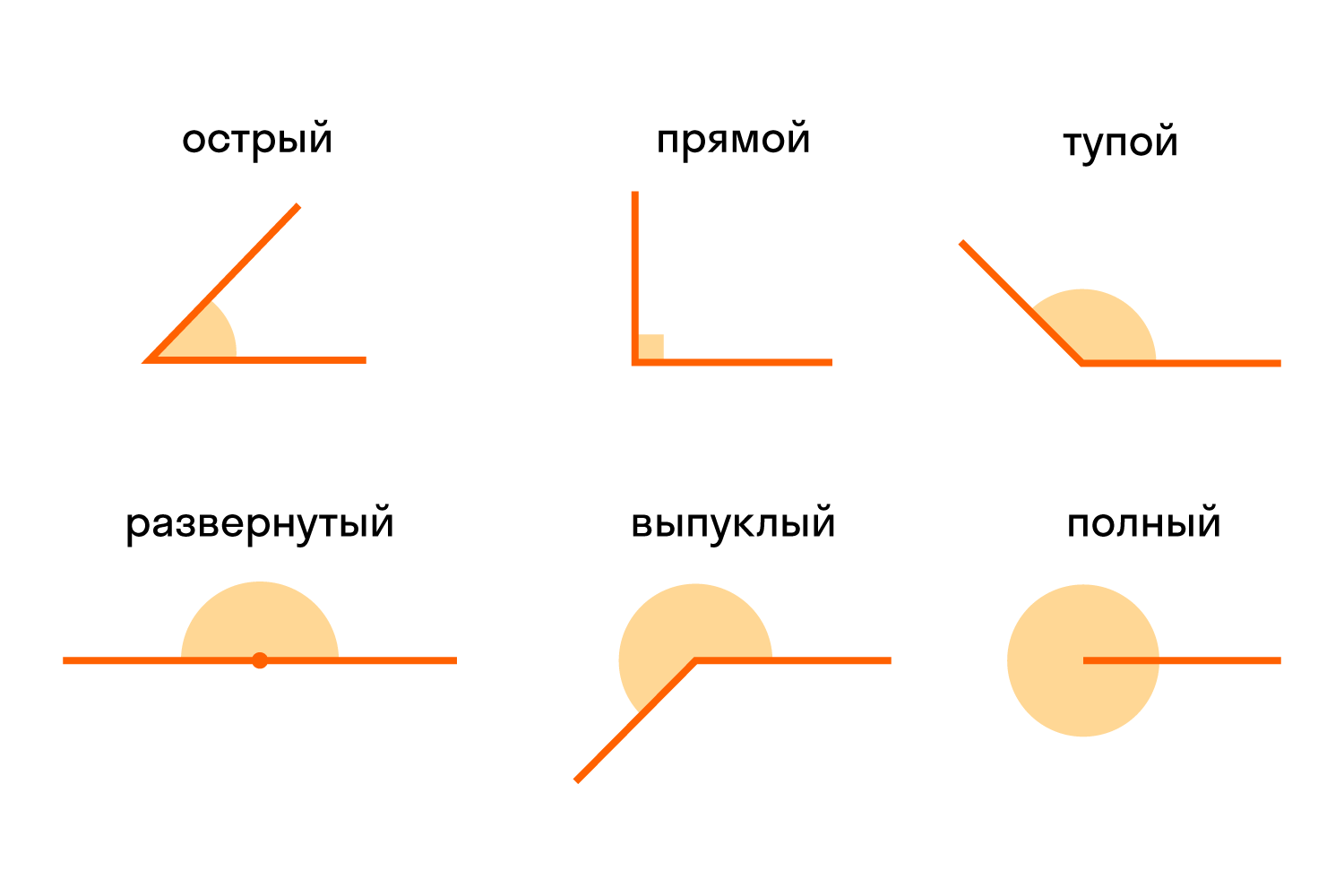
Виды углов
Есть разные типы углов и у каждого своё название:
- острый
- прямой
- тупой
- развернутый
- выпуклый
- полный
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.
Острый угол — это угол, который меньше прямого угла, то есть
Сравнение углов
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:
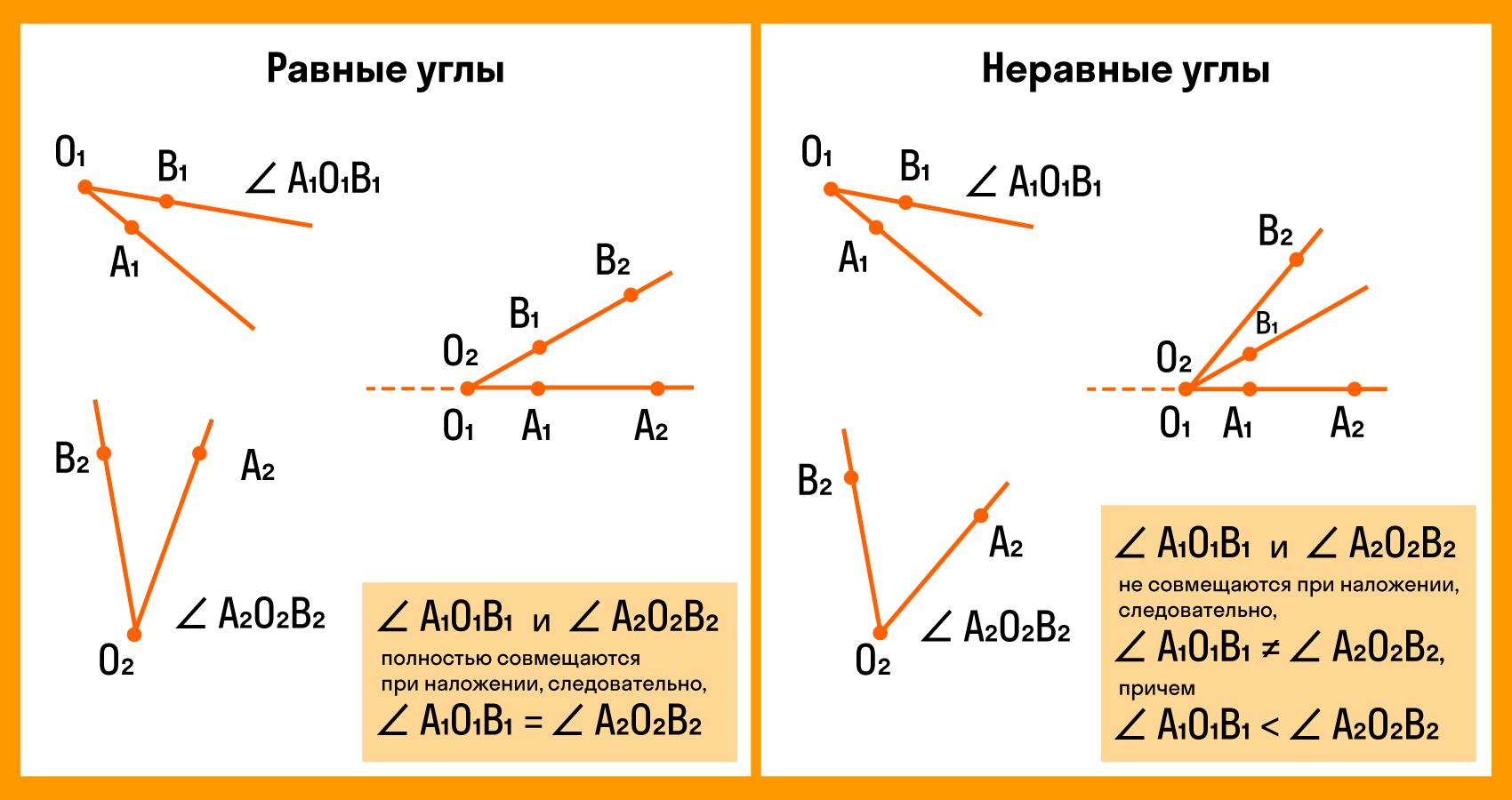
При этом развернутые углы всегда являются равными.
Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:
- Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.
- Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.
Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.
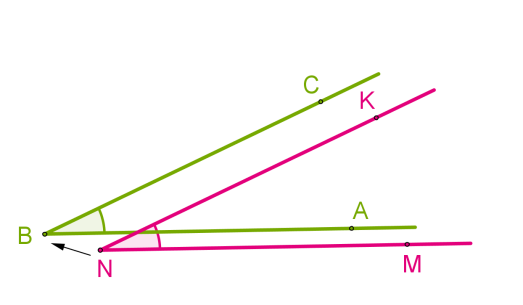
Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶
Как правильно измерять углы
Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Обозначается — 0.
Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.
Минута — 1/60 часть градуса. Обозначается — ´.
Секунда — 1/60 часть минуты. Обозначается — ´´.
Градус состоит из 3600 секунд, то есть: 1° = 60′ = 3600′.
Как происходит измерение угла: сначала измеряются стороны угла, а после его внутренняя область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.
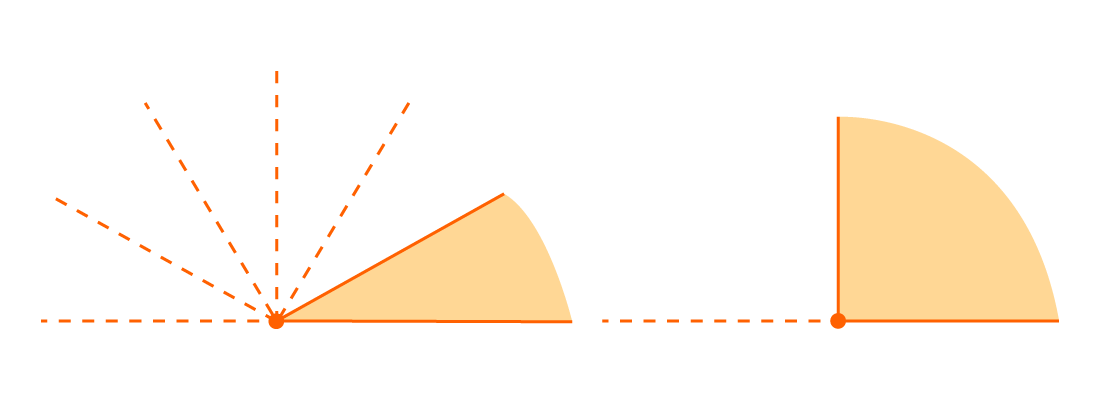
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠ A O B = ∠ A O C + ∠ D O B = 45° + 30° + 60° = 135 °.
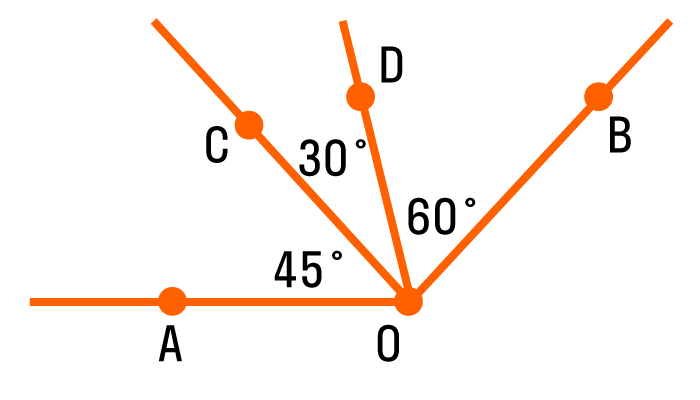
Угол называется прямым, если он равен 90°, а острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол имеет 180°.
Равные углы имеют равную градусную меру.
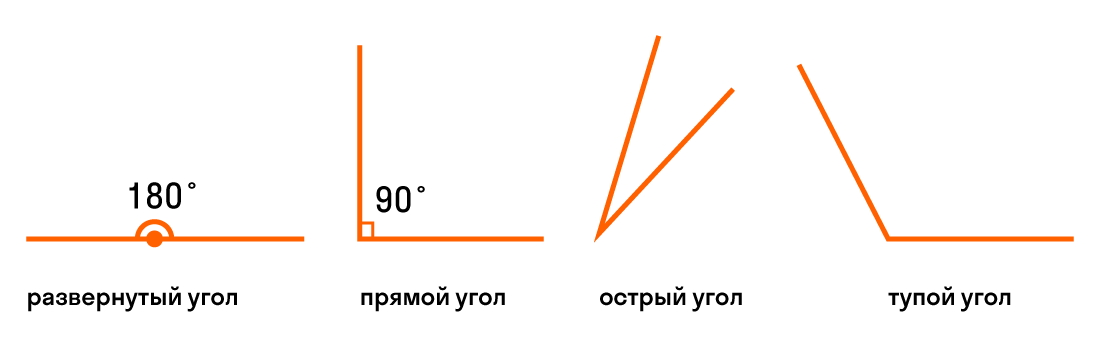
Обозначение углов на чертеже
Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать дуги, углы и прочие фигурки, придумали даже отдельное направление — геометрический чертеж.
Задачи с углами могут быть разными и не всегда есть возможность правильно изобразить и отметить угол. Вот, что важно запомнить при обозначении лучей и углов:
- Равные углы обозначают одинаковым количеством дуг.
- Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.
- Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.
На чертеже отмечены острые, равные и неравные углы.
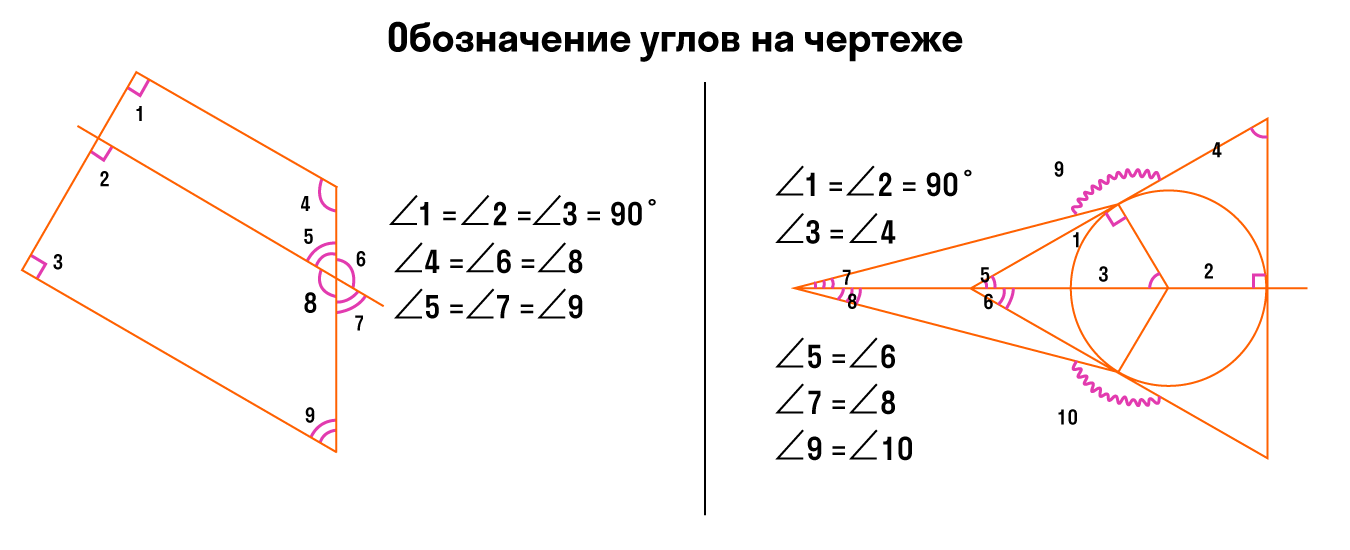
Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом необязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.
Внутренние односторонние углы – определение, свойство, правило
Наглядная геометрия 7 класс. Опорный конспект № 3 Параллельные прямые.

В геометрии нельзя «на глазок» определить, параллельны прямые или нет. Это может быть либо дано, либо доказано. Вы уже знаете, что на плоскости справедлива теорема: «Две прямые, перпендикулярные третьей, параллельны между собой».
Есть еще три признака параллельности прямых, которые можно объединить в одну теорему, она так и называется: «Признаки параллельности прямых». Данные признаки связаны с углами, которые образуются при пересечении двух прямых третьей прямой. Это так называемые накрест лежащие углы, соответственные углы и односторонние углы.
Оказывается, что если накрест лежащие углы равны, или соответственные углы равны, или сумма односторонних углов равна 180°, то прямые будут параллельны.
Справедливы и обратные утверждения. Если даны две заведомо параллельные прямые, которые пересечены третьей, то накрест лежащие углы равны, соответственные углы равны и сумма односторонних углов равна 180°.
Ранее мы доказали, что через точку вне прямой можно провести единственную прямую, перпендикулярную данной. Можно также доказать, что через точку, не лежащую на прямой, можно провести прямую, параллельную данной. А вот доказать, что такая прямая — единственная, нельзя! Утверждение «Через точку, не лежащую на прямой, можно провести ЕДИНСТВЕННУЮ прямую, параллельную данной» называется аксиомой параллельных прямых. У Евклида эта аксиома называлась пятым постулатом.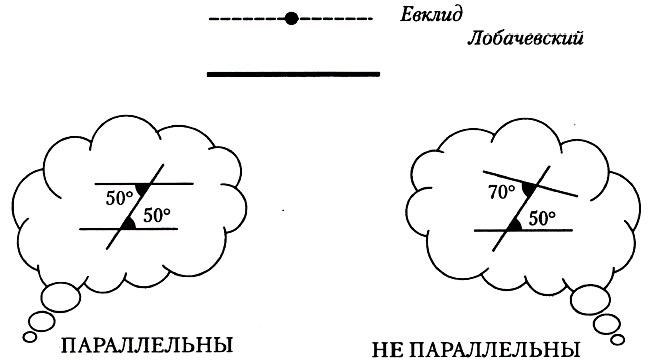
На протяжении двух тысячелетий это утверждение вызывало захватывающие и драматичные споры между такими знаменитыми учеными, как Лобачевский, Гаусс и другие. Споры состояли в том, можно или нельзя доказать этот пятый постулат Евклида на основании уже известных теорем. В конце концов работы в этом направлении привели к полному пересмотру научных представлений о геометрии Вселенной.

При пересечении двух прямых третьей, которая называется секущей, образуется 4 пары накрест лежащих углов, 4 пары соответственных и 4 пары односторонних.
3 и 5; 4 и 6 — внутренние накрест лежащие углы;
1 и 7; 2 и 8 — внешние накрест лежащие углы;
1 и 5; 2 и 6; 4 и 8; 3 и 7 — соответственные углы;
3 и 6; 4 и 5 — внутренние односторонние углы;
2 и 7; 1 и 8 — внешние односторонние углы.
Признаки параллельности прямых. Если накрест лежащие углы равны, ши соответственные углы равны, ши сумма односторонних углов равна 180°, то прямые параллельны. В первую очередь нужно доказать, что если накрест лежащие углы равны, то прямые параллельны. Доказательство опирается на уже доказанное нами свойство: две прямые, перпендикулярные третьей, параллельны между собой. Из середины отрезка секущей опускают перпендикуляр на одну из параллельных прямых. Затем перпендикуляр продляют до пересечения со второй прямой. Из равенства полученных треугольников следует, что прямая, проходящая через перпендикуляр, будет перпендикулярна и второй прямой. Дальнейшее просто.
Через точку, не лежащую на данной прямой, МОЖНО провести прямую, параллельную данной. Опустив перпендикуляр из точки на прямую, а затем, восставив перпендикуляр к проведенной прямой, получим две прямые, перпендикулярные третьей, которые будут параллельны. А вот доказать, что такая прямая единственная, нельзя. Поэтому справедлива АКСИОМА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ: «Через точку, не лежащую на данной прямой, проходит ЕДИНСТВЕННАЯ прямая, параллельная данной».
Теорема о двух прямых, параллельных третьей. Две прямые, параллельные третьей, параллельны между собой. Если бы они пересекались, то через одну точку проходили бы две прямые, параллельные третьей.
Теорема о пересечении параллельных прямых. Если на плоскости прямая пересекает одну из двух параллельных прямых, то она пересекает и другую. Если бы эта прямая не пересекала вторую прямую, то она была бы ей параллельна. Но тогда через одну точку проходили бы две прямые, параллельные третьей. А это невозможно.
Свойства углов при параллельных прямых и секущей. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны, соответственные углы равны и сумма односторонних углов равна 180°. В первую очередь нужно доказать, что если прямые параллельны, то накрест лежащие углы равны. Пусть прямые параллельны, а накрест лежащие углы 1 и 2 не равны. Отложим угол, равный углу 2, как показано на рисунке. Получим еще одну прямую, параллельную нижней прямой (если накрест лежащие углы равны, то прямые параллельны). Но через точку нельзя провести две прямые, параллельные третьей. Значит, наше предположение неверно, и накрест лежащие углы равны. Остальное несложно.
Из указанных свойств параллельных прямых вытекает важное следствие: перпендикуляр к одной из параллельных прямых будет перпендикуляром и к другой. Доказательство следует из равенства соответственных углов.
Теорема об углах с соответственно параллельными сторонами. Углы с соответственно параллельными сторонами равны, если они одновременно острые ши одновременно тупые, и в сумме составляют 180°, если один из них острый, а другой — тупой. Продлив стороны данных углов, получим две пары равных соответственных углов, откуда ∠1 = ∠2. Продлив сторону угла 1 за его вершину, получим доказательство второй части теоремы.
Теорема об углах с соответственно перпендикулярными сторонами. Углы с соответственно перпендикулярными сторонами равны, если они одновременно острые или одновременно тупые, и в сумме составляют 180°, если один из них острый, а другой — тупой. Проведя перпендикулярные лучи из вершины угла 1, получим, что углы 2 и 3 равны и углы 3 и 1 дополняют один и тот же угол 4 до 90°. Значит, ∠1 = ∠3, ∠1 = ∠2. Продлив сторону угла 2 за его вершину, получим доказательство второй части теоремы.
Это опорный конспект № 3 по геометрии в 7 классе «Параллельные прямые (опорный конспект)». Выберите дальнейшие действия:
Геометрия. 7 класс
Конспект урока
Свойства параллельных прямых
Перечень рассматриваемых вопросов:
- Углы, образованные при пересечении двух прямых секущей.
- Доказательство свойств параллельных прямых и их применение при решении задач.
- Формулирование теоремы об углах с соответственно параллельными сторонами.
Две прямые на плоскости называются параллельными, если они не пересекаются.
Утверждение, обратное данной теореме– это утверждение, в котором условие является заключением теоремы, а заключение – условием теоремы.
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Ранее мы узнали и научились применять признаки параллельности прямых.
Рассмотрим утверждения, обратные к теоремам, выражающим признаки параллельности двух прямых.
В любой теореме есть две части: условие (это то, что дано)и заключение (это то, что требуется доказать).
Утверждением, обратным данному, называется утверждение, в котором условием является заключение, а заключением – условие.
Итак, вспомним один из признаков параллельности прямых. Если при пересечении двух прямых секущей накрест лежащие углы, образованные этими прямыми и секущей, равны (это условие), то прямые параллельны (заключение).

Сформулируем и докажем обратное утверждение.
Если две параллельные прямые пересечены секущей, то накрест лежащие углы,образованные этими прямыми и секущей,равны.
∠1 и ∠2 – накрест лежащие.
Доказательство:( метод от противного):

Отложим ∠PMN =∠2 (накрест лежащие) → МР║b→ через точку М проходит 2 параллельные прямые прямой b (МР║b– доказательство;a║b– условие).→∠1=∠2.
Это противоречит теореме о единственности прямой параллельной данной и проходящей через точку.
Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.

С пересекает а, значит, и пересекает параллельную ей прямую b(по следствию из аксиомы параллельных прямых).→ с – секущая к прямым а и b→∠1 = ∠2 = 90° (по только что доказанному свойству параллельных прямых).→ с ┴ b.
Что и требовалось доказать.
Вспомним ещё один признак параллельности двух прямых. Если при пересечении двух прямых секущей соответственные углы равны(это условие), то прямые параллельны(заключение).

Сформулируем и докажем обратное утверждение
Если две параллельные прямые пересечены секущей, то соответственные углы, образованные этими прямыми и секущей, равны.

Дано:
Доказать:
По условию a║b→∠1 = ∠3 (накрест лежащие углы). → ∠2 = ∠3 (вертикальные углы).
Значит, ∠1 = ∠2, что и требовалось доказать.
Вспомним ещё один признак параллельности двух прямых. Если при пересечении двух прямых секущей сумма односторонних углов, образованных этими прямыми и секущей, равна 180° (условие), то прямые параллельны (заключение).

Сформулируем и докажем обратное утверждение.
Если две параллельные прямые пересечены секущей, то сумма односторонних углов, образованных этими прямыми и секущей, равна 180°.

Дано:a║b,
Доказать:
Доказательство:
По условию a║b→∠1=∠2 ‑соответственные углы, (в силу предыдущей теоремы).
∠2+∠4=180° (по свойству смежных углов).
→ ∠1+∠4= 180°,что и требовалось доказать.
Материал для углубленного изучения темы.
Задача на доказательство.
Прямая m пересекает параллельные прямые а и b в точках А и В. Прямая р, проходящая через середину отрезка АВ, точку О, пересекает прямые а и b в точках С и D.
Докажем, что ОС=ОD.
По условию дано: а ║b, рՈа= А, рՈb = В, mՈа = D, mՈb = C.
Доказать: ОС = ОD.
Доказательство: рассмотрим, образовавшиеся при построении, треугольники AOD и BOC. Они равны по 2 признаку равенства треугольников, т.к. АО=ВО (О– середина отрезка АВ по условию); ∠1=∠2(накрест лежащие углы); ∠3=∠4 (вертикальные углы). →Все элементы равных треугольников соответственно равны → ОС=ОD. Что и требовалось доказать.

Разбор заданий тренировочного модуля.
1. Три прямых а,р,с пересечены прямой k, при этом образуются соответственные углы: ∠1= 30°,∠2 = 40°,∠3= 30°,как показано на рисунке. Какие из прямых параллельны?

На рисунке изображены прямые а, р, с, которые пересечены секущей k. При этом углы 1,2,3 соответственные. По условию: ∠3= ∠1= 30°,∠2 ≠ ∠1,∠2 ≠ ∠3.
Следовательно, прямые а и р параллельные, прямые а и с, р и с не параллельные(по свойствам параллельных прямых).
2. На рисунке прямые а║b, при этомMO и ЕО – биссектрисы углов М и Е соответственно, пересекаются в точке О. Чему равна градусная мера угла МОЕ, если сумма углов в треугольнике равна 180°?

По условию а║b→∠М+∠Е=180° (по теореме о параллельных прямых об односторонних углах). Т.к. MO и ЕО – биссектрисы углов М и Е →∠М = 2∠ОМЕ,
∠М+∠Е =2∠ОМЕ +2∠МЕО =180°.
По условию сумма углов в треугольнике равна 180° → в ∆МОЕ.





