Как перевести десятичную дробь в обыкновенную
Вот, казалось бы, перевод десятичной дроби в обычную — элементарная тема, но многие ученики её не понимают! Поэтому сегодня мы подробно рассмотрим сразу несколько алгоритмов, с помощью которых вы разберётесь с любыми дробями буквально за секунду.
Напомню, что существует как минимум две формы записи одной и той же дроби: обыкновенная и десятичная. Десятичные дроби — это всевозможные конструкции вида 0,75; 1,33; и даже −7,41. А вот примеры обыкновенных дробей, которые выражают те же самые числа:
Сейчас разберёмся: как от десятичной записи перейти к обычной? И самое главное: как сделать это максимально быстро?
Основной алгоритм
На самом деле существует как минимум два алгоритма. И мы сейчас рассмотрим оба. Начнём с первого — самого простого и понятного.
Чтобы перевести десятичную дробь в обыкновенную, необходимо выполнить три шага:
-
Переписать исходную дробь в виде новой дроби: в числителе останется исходная десятичная дробь, а в знаменателе нужно поставить единицу. При этом знак исходного числа также помещается в числитель. Например:
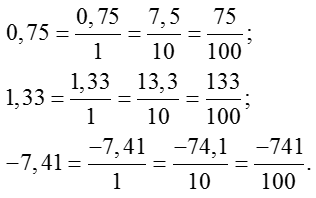 Алгоритм перехода к обычным дробям
Алгоритм перехода к обычным дробямВажное замечание по поводу отрицательных чисел. Если в исходном примере перед десятичной дробью стоит знак «минус», то и на выходе перед обыкновенной дробью тоже должен стоять «минус». Вот ещё несколько примеров:
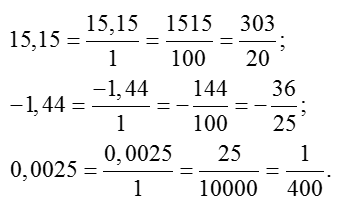 Примеры перехода от десятичной записи дробей к обычной
Примеры перехода от десятичной записи дробей к обычной
Особое внимание хотелось бы обратить на последний пример. Как видим, в дроби 0,0025 присутствует много нулей после запятой. Из-за этого приходится аж целых четыре раза умножать числитель и знаменатель на 10. Можно ли как-то упростить алгоритм в этом случае?
Конечно, можно. И сейчас мы рассмотрим альтернативный алгоритм — он чуть более сложен для восприятия, но после небольшой практики работает намного быстрее стандартного.
Более быстрый способ
В данном алгоритме также 3 шага. Чтобы получить обычную дробь из десятичной, нужно выполнить следующее:
Вот и всё! На первый взгляд, эта схема сложнее предыдущей. Но на самом деле он и проще, и быстрее. Судите сами:
Как видим, в дроби 0,64 после запятой стоит две цифры — 6 и 4. Поэтому $n=2$. Если убрать запятую и нули слева (в данном случае — всего один ноль), то получим число 64. Переходим ко второму шагу: $<<10>^
Ещё один пример:
Здесь всё чуть сложнее. Во-первых, цифр после запятой уже 3 штуки, т.е. $n=3$, поэтому делить придётся на $<<10>^
Наконец, последний пример:
Особенность этой дроби — наличие целой части. Поэтому на выходе у нас получается неправильная дробь 47/25. Можно, конечно, попытаться разделить 47 на 25 с остатком и таким образом вновь выделить целую часть. Но зачем усложнять себе жизнь, если это можно сделать ещё на этапе преобразований? Что ж, разберёмся.
Что делать с целой частью
На самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой.
Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88. Она легко преобразуется:
Затем вспоминаем про «утерянную» единицу и дописываем её спереди:
Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз. Ещё парочка примеров:
В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:)
В заключение хотел бы рассмотреть ещё один приём, который многим помогает.
Преобразования «на слух»
Давайте задумаемся о том, что вообще такое десятичная дробь. Точнее, как мы её читаем. Например, число 0,64 — мы читаем его как «ноль целых, 64 сотых», правильно? Ну, или просто «64 сотых». Ключевое слово здесь — «сотых», т.е. число 100.
А что насчёт 0,004? Это же «ноль целых, 4 тысячных» или просто «четыре тысячных». Так или иначе, ключевое слово — «тысячных», т.е. 1000.
Ну и что в этом такого? А то, что именно эти числа в итоге «всплывают» в знаменателях на втором этапе алгоритма. Т.е. 0,004 — это «четыре тысячных» или «4 разделить на 1000»:
Попробуйте потренироваться сами — это очень просто. Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому
А какое-нибудь 1,125 — это «1 целая, 125 тысячных», поэтому
В последнем примере, конечно, кто-то возразит, мол, не всякому ученику очевидно, что 1000 делится на 125. Но здесь нужно помнить, что 1000 = 10 3 , а 10 = 2 ∙ 5, поэтому
[begin
Таким образом, любая степень десятки раскладывается лишь на множители 2 и 5 — именно эти множители нужно искать и в числителе, чтобы в итоге всё сократилось.
На этом урок окончен. Переходим к более сложной обратной операции — см. «Переход от обыкновенной дроби к десятичной».
Перевод десятичной дроби в обыкновенную и наоборот: правило, примеры
Бывает, что для удобства расчетов нужно перевести обыкновенную дробь в десятичную и наоборот. О том, как это делать, мы поговорим в данной статье. Разберем правила перевода обыкновенных дробей в десятичные и обратно, а также приведем примеры.
Перевод обыкновенных дробей в десятичные
Мы будем рассматривать перевод обыкновенных дробей в десятичные, придерживаясь определенной последовательности. Во первых, рассмотрим, как в десятичные переводятся обыкновенные дроби со знаменателем, кратным 10: 10, 100, 1000 и т.д.Дроби с такими знаменателями, по сути, являются, более громоздкой записью десятичных дробей.
Далее мы рассмотрим, как переводить в десятичные дроби обыкновенные дроби с любым, не только кратным 10, знаменателем. Отметим, что при обращении обыкновенных дробей в десятичные получаются не только конечные десятичные, но и бесконечные периодические десятичные дроби.
Перевод обыкновенных дробей со знаменателями 10, 100, 1000 и т.д. в десятичные дроби
Первым делом, скажем, что некоторые дроби нуждаются в определенной подготовке перед обращением в десятичный вид. В чем она заключается? Перед цифрой, стоящей в числителе, необходимо дописать столько нулей, чтобы количество цифр числителя стало равно числу нулей в знаменателе. Например, для дроби 3100 число 0 необходимо один раз дописать слева от 3 в числителе. Дробь 610, согласно изложенному выше правилу, не нуждается в доработке.
Рассмотрим еще один пример, после чего сформулируем правило, которым особенно удобно пользоваться на первых порах, пока опыта в обращении дробей не так много. Так, дробь 1610000 после дописывания нулей в числителе будет иметь вид 001510000.
Как перевести обыкновенную дробь со знаменателем 10, 100, 1000 и т.д. в десятичную?
Правило перевода обыкновенных правильных дробей в десятичные
- Записываем 0 и ставим после него запятую.
- Записываем число из числителя, которое получилось после дописывания нулей.
Теперь перейдем к примерам.
Пример 1. Перевод обыкновенных дробей в десятичные
Переведем обыкновенную дробь 39 100 в десятичную.
Сначала смотрим на дробь и видим, что никаких подготовительных действий проводить не нужно – количество цифр в числителе совпадает с количеством нулей в знаменателе.
Следуя правилу, записываем 0 , ставим после него десятичную запятую и записываем число из числителя. Получаем десятичную дробь 0 , 39 .
Разберем решение еще одного примера по этой теме.
Пример 2. Перевод обыкновенных дробей в десятичные
Запишем дробь 105 10000000 в виде десятичной дроби.
Количество нулей в знаменателе равно 7 , а в числителе только три цифры. Допишем перед числом в числителе еще 4 нуля:
Теперь записываем 0 , ставим после него десятичную запятую и записываем число из числителя. Получаем десятичную дробь 0 , 0000105 .
Рассмотренные во всех примерах дроби – обыкновенные правильные дроби. Но как перевести неправильную обыкновенную дробь в десятичную? Сразу скажем, что необходимость в подготовке с дописыванием нулей для таких дробей отпадает. Сформулируем правило.
Правило перевода обыкновенных неправильных дробей в десятичные
- Записываем число, которое находится в числителе.
- Десятичной запятой отделяем столько цифр справа, сколько нулей есть в знаменателе исходной обыкновенной дроби.
Ниже приведем пример на использование этого правила.
Пример 3. Перевод обыкновенных дробей в десятичные
Переведем дробь 56888038009 100000 из обыкновенной неправильной в десятичную.
Сначала запишем число из числителя:
Теперь справа отделим десятичной запятой пять цифр (количество нулей в знаменателе – пять). Получим:
Следующий вопрос, который закономерно возникает: как перевести в десятичную дробь смешанное число, если знаменателем его дробной части является число 10, 100, 1000 и т.д. Для обращения в десятичную дробь такого числа можно воспользоваться следующим правилом.
Правило перевода смешанных чисел в десятичные дроби
- Выполняем подготовку дробной части числа, если это необходимо.
- Записываем целую часть исходного числа и ставим после него запятую.
- Записываем число из числителя дробной части вместе с дописанными нулями.
Обратимся к примеру.
Пример 4. Перевод смешанных чисел в десятичные дроби
Переведем смешанное число 23 17 10000 в десятичную дробь.
В дробной части имеем выражение 17 10000 . Выполним его подготовку и допишем слева от числителя еще два нуля. Получим: 0017 10000 .
Теперь записываем целую часть числа и ставим после него запятую: 23 , . .
После запятой записываем число из числителя вместе с нулями. Получаем результат:
23 17 10000 = 23 , 0017
Перевод обыкновенных дробей в конечные и бесконечные периодические дроби
Конечно, можно переводить в десятичные дроби и обыкновенные дроби со знаменателем, не равным 10, 100, 1000 и т.д.
Часто дробь можно легко привести к новому знаменателю, а затем уже воспользоваться правилом, изложенным в первом пункте данной статьи. Например, достаточно умножить числитель и знаменатель дроби 25 на 2, и мы получим дробь 410, которая легко приводится к десятичному виду 0,4.
Однако такой способ перевода обыкновенной дроби в десятичную удается использовать не всегда. Ниже рассмотрим, как поступать, если применить рассмотренный способ невозможно.
Принципиально новый способ обращения обыкновенной дроби в десятичную сводится к делению числителя на знаменатель столбиком. Эта операция очень похожа на деление натуральных чисел столбиком, но имеет свои особенности.
Числитель при делении представляется в виде десятичной дроби – справа от последней цифры числителя ставится запятая и дописываются нули. В получившемся частном десятичная запятая ставится тогда, когда заканчивается деление целой части числителя. Как именно работает этот способ, станет понятно после рассмотрения примеров.
Пример 5. Перевод обыкновенных дробей в десятичные
Переведем обыкновенную дробь 621 4 в десятичный вид.
Представим число 621 из числителя в виде десятичной дроби, добавив после запятой несколько нулей. 621 = 621 , 00
Теперь разделим столбиком 621 , 00 на 4 . Первые три шага деления будут такими же, как при делении натуральных чисел, и мы получим.
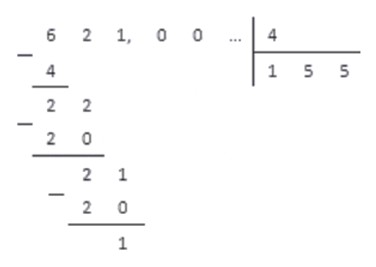
Когда мы добрались до десятичной запятой в делимом, а остаток отличен от нуля, ставим в частном десятичную запятую, и продолжаем делить, не обращая более внимания на запятую в делимом.
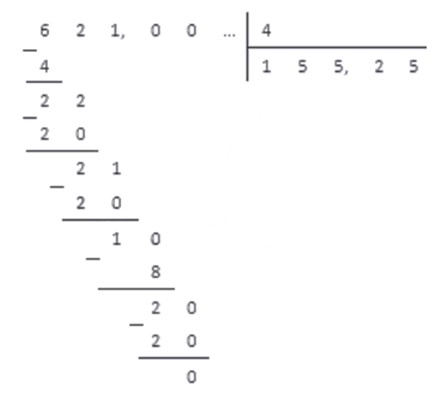
В итоге мы получаем десятичную дробь 155 , 25 , которая и является результатом обращения обыкновенной дроби 621 4
Рассмотрим решение еще одного примера, чтобы закрепить материал.
Пример 6. Перевод обыкновенных дробей в десятичные
Обратим обыкновенную дробь 21 800 .
Для этого в столбик разделим дробь 21 , 000 на 800 . Деление целой части закончится на первом же шаге, поэтому сразу после него ставим в частном десятичную запятую и продолжаем деление, не обращая внимания на запятую в делимом до того момента, пока не получим остаток, равный нулю.
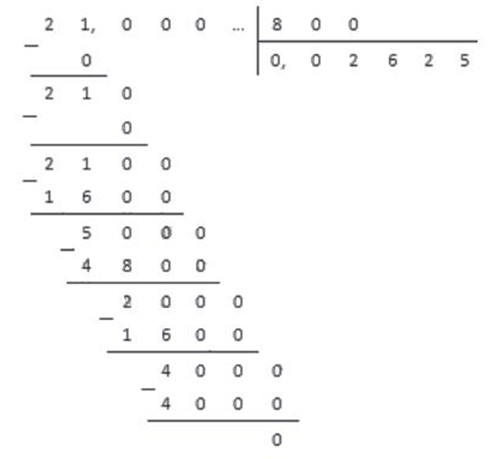
В результате мы получили: 21 800 = 0 , 02625 .
Но как быть, если при делении мы так и не получим в остатке 0. В таких случаях деление можно продолжать бесконечно долго. Однако, начиная с определенного шага, остатки будут периодически повторяться. Соответственно, будут повторяться и цифры в частном. Это значит, что обыкновенная дробь переводится в десятичную бесконечную периодическую дробь. Проиллюстрируем сказанное на примере.
Пример 7. Перевод обыкновенных дробей в десятичные
Обратим обыкновенную дробь 19 44 в десятичную. Для этого выполним деление столбиком.
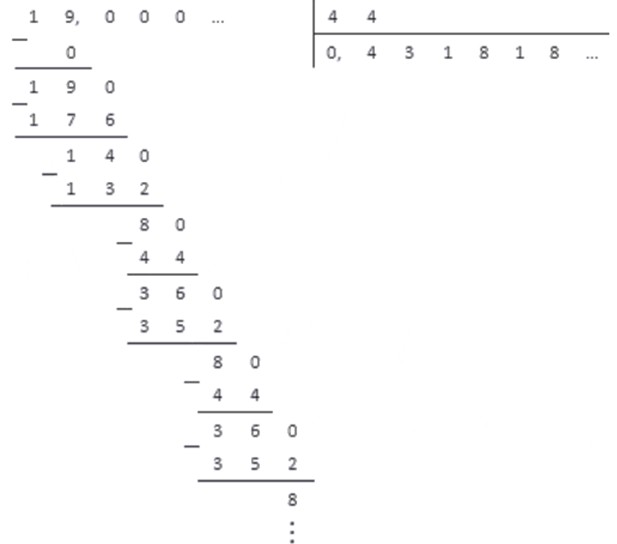
Мы видим, что при делении повторяются остатки 8 и 36 . При этом в частном повторяются цифры 1 и 8 . Это и есть период в десятичной дроби. При записи эти цифры берутся в скобки.
Таким образом, исходная обыкновенная дробь переведена в бесконечную периодическую десятичную дробь.
19 44 = 0 , 43 ( 18 ) .
Пусть перед нами несократимая обыкновенная дробь. К какому виду она приведется? Какие обыкновенные дроби переводятся в конечные десятичные, а какие – в бесконечные периодические?
Во первых, скажем, что если дробь удается привести к одному из знаменателей 10, 100, 1000. то она будет иметь вид конечной десятичной дроби. Чтобы дробь приводилась к одному из таких знаменателей, ее знаменатель должен быть делителем хотя бы одного из чисел 10, 100, 1000 и т.д. Из правил разложения чисел на простые множители следует, что делитель чисел 10, 100, 1000 и т.д. должен, при разложении на простые множители, содержать лишь числа 2 и 5.
- Обыкновенную дробь можно привести к виду конечной десятичной дроби, если ее знаменатель можно разложить на простые множители 2 и 5.
- Если кроме чисел 2 и 5 в разложении знаменателя присутствуют другие простые числа, дробь приводится к виду бесконечной периодической десятичной дроби.
Пример 8. Перевод обыкновенных дробей в десятичные
Какая из данных дробей 47 20 , 7 12 , 21 56 , 31 17 переводится в конечную десятичную дробь, а какая – только в периодическую. Дадим ответ на этот вопрос, не выполняя непосредственно перевода обыкновенной дроби в десятичную.
Дробь 47 20 , как легко заметить, умножением числителя и знаменателя на 5 приводится к новому знаменателю 100 .
47 20 = 235 100 . Отсюда делаем вывод, что данная дробь переводится в конечную десятичную дробь.
Разложение знаменателя дроби 7 12 на множители дает 12 = 2 · 2 · 3 . Так как простой множитель 3 отличен от 2 и от 5 , данная дробь не может быть представлена в виде конечной десятичной дроби, а будет иметь вид бесконечной периодической дроби.
Дробь 21 56 , во-первых, нужно сократить. После сокращения на 7 получим несократимую дробь 3 8 , разложение знаменателя которой на множители дает 8 = 2 · 2 · 2 . Следовательно, это конечная десятичная дробь.
В случае с дробью 31 17 разложение знаменателя на множители представляет собой само простое число 17 . Соответственно, эту дробь можно обратить в бесконечную периодическую десятичную дробь.
Обыкновенную дробь нельзя перевести в бесконечную и непериодическую десятичную дробь
Выше мы говорили только о конечных и бесконечных периодических дробях. Но может ли какая-либо обыкновенная дробь быть обращена в вид бесконечной непериодической дроби?
При переводе бесконечной дроби в десятичную получается либо конечная десятичная дробь, либо бесконечная периодическая десятичная дробь.
Остаток от деления всегда меньше делителя. Другими словами, согласно теореме о делимости, если мы делим какое-то натуральное число на число q, то остаток деления в любом случае не может быть больше, чем q-1. После окончания деления возможна одна из следующих ситуаций:
- Мы получаем в остатке 0, и на этом деление заканчивается.
- Мы получаем остаток, который при последующем делении повторяется, в результате мы имеем бесконечную периодическую дробь.
Иных вариантов при обращении обыкновенной дроби в десятичную не может быть. Скажем также, что длина периода (количество цифр) в бесконечной периодической дроби всегда меньше, чем число цифр в знаменателе соответствующей обыкновенной дроби.
Перевод десятичных дробей в обыкновенные дроби
Теперь пришло время рассмотреть обратный процесс перевода десятичной дроби в обыкновенную. Сформулируем правило перевода, которое включает три этапа. Как перевести десятичную дробь в обыкновенную?
Правило перевода десятичных дробей в обыкновенные дроби
- В числитель записываем число из исходной десятичной дроби, отбросив запятую и все нули слева, если они есть.
- В знаменатель записываем единицу и за ней столько нулей, сколько цифр есть в исходной десятичной дроби после запятой.
- При необходимости сокращаем полученную обыкновенную дробь.
Рассмотрим применение данного правила на примерах.
Пример 8. Перевод десятичных дробей в обыкновенные
Представим число 3 , 025 в виде обыкновенной дроби.
- В числитель записываем саму десятичную дробь, отбросив запятую: 3025 .
- В знаменателе пишем единицу, а после нее три нуля – именно столько цифр содержится в исходной дроби после запятой: 3025 1000 .
- Полученную дробь 3025 1000 можно сократить на 25 , в результате чего мы получим: 3025 1000 = 121 40 .
Переведем дробь 0 , 0017 из десятичных в обыкновенные.
- В числителе запишем дробь 0 , 0017 , отбросив запятую и нули слева. Получится 17 .
- В знаменатель записываем единицу, а после нее пишем четыре нуля: 17 10000 . Данная дробь несократима.
Если в десятичной дроби есть целая часть, то такую дробь можно сразу перевести в смешанное число. Как это сделать?
Сформулируем еще одно правило.
Правило перевода десятичных дробей в смешанные числа.
- Число, стоящее в дроби до запятой, записываем как целая часть смешанного числа.
- В числителе записываем число, стоящее в дроби после запятой, отбросив нули слева, если они есть.
- В знаменателе дробной части дописываем единицу и столько нулей, сколько цифр есть в дробной части после запятой.
Обратимся к примеру
Пример 10. Перевод десятичной дроби в смешанное число
Представим дробь 155 , 06005 в виде смешанного числа.
- Записываем число 155 , как целую часть.
- В числителе записываем цифры после запятой, отбросив нуль.
- В знаменателе записываем единицу и пять нулей
Поучаем смешанное число: 155 6005 100000
Дробную часть можно сократить на 5 . Сокращаем, и получаем финальный результат:
155 , 06005 = 155 1201 20000
Перевод бесконечных периодических десятичных дробей в обыкновенные дроби
Разберем на примерах, как осуществлять перевод периодических десятичных дробей в обыкновенные. Прежде чем начать, уточним: любую периодическую десятичную дробь можно перевести в обыкновенную.
Самый простой случай – период дроби равен нулю. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.
Пример 11. Перевод периодической десятичной дроби в обыкновенную
Обратим периодическую дробь 3 , 75 ( 0 ) .
Отбросив нули справа, получим конечную десятичную дробь 3 , 75 .
Обращая данную дробь в обыкновенную по алгоритму, разобранному в предыдущих пунктах, получаем:
3 , 75 ( 0 ) = 3 , 75 = 375 100 = 15 4 .
Как быть, если период дроби отличен от нуля? Периодическую часть следует рассматривать как сумму членов геометрический прогрессии, которая убывает. Поясним это на примере:
0 , ( 74 ) = 0 , 74 + 0 , 0074 + 0 , 000074 + 0 , 00000074 + . .
Для суммы членов бесконечной убывающей геометрической прогрессии существует формула. Если первый член прогрессии равен b , а знаменатель q таков, что 0 q 1 , то сумма равна b 1 – q .
Рассмотрим несколько примеров с применением данной формулы.
Пример 12. Перевод периодической десятичной дроби в обыкновенную
Пусть у нас есть периодическая дробь 0 , ( 8 ) и нам нужно перевести ее в обыкновенную.
0 , ( 8 ) = 0 , 8 + 0 , 08 + 0 , 008 + . .
Здесь мы имеем бесконечную убывающую геометрическую прогрессию с первым членом 0 , 8 и знаменателем 0 , 1 .
0 , ( 8 ) = 0 , 8 + 0 , 08 + 0 , 008 + . . = 0 , 8 1 – 0 , 1 = 0 , 8 0 , 9 = 8 9
Это и есть искомая обыкновенная дробь.
Для закрепления материала рассмотрим еще один пример.
Пример 13. Перевод периодической десятичной дроби в обыкновенную
Обратим дробь 0 , 43 ( 18 ) .
Сначала записываем дробь в виде бесконечной суммы:
0 , 43 ( 18 ) = 0 , 43 + ( 0 , 0018 + 0 , 000018 + 0 , 00000018 . . )
Рассмотрим слагаемые в скобках. Эту геометрическую прогрессию можно представить в следующем виде:
0 , 0018 + 0 , 000018 + 0 , 00000018 . . = 0 , 0018 1 – 0 , 01 = 0 , 0018 0 , 99 = 18 9900 .
Полученное прибавляем к конечной дроби 0 , 43 = 43 100 и получаем результат:
0 , 43 ( 18 ) = 43 100 + 18 9900
После сложения данных дробей и сокращения получим окончательный ответ:
0 , 43 ( 18 ) = 19 44
В завершение данной статьи скажем, что непериодические бесконечный десятичные дроби нельзя перевести в вид обыкновенных дробей.
Как перевести дробь в десятичную и наоборот

О чем эта статья:
Что такое дробь: понятие
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
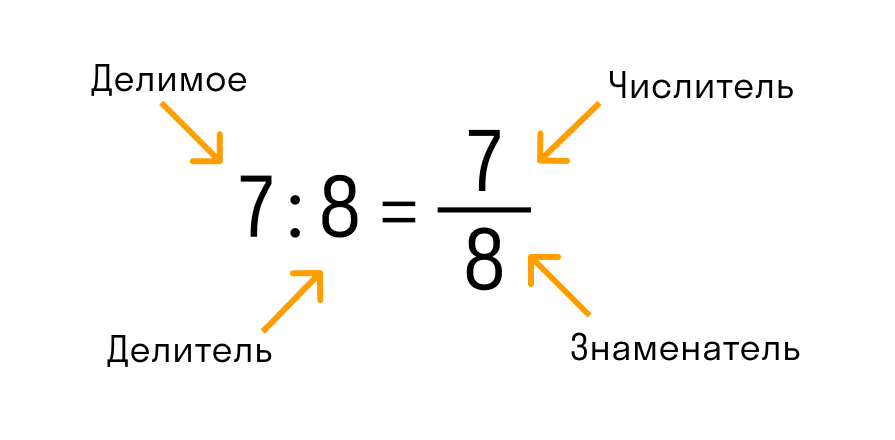
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 5/9 или (1,5 – 0,2)/15.
- Алгебраические — состоят из переменных. Например, (x + y)/(x – y). В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как «пять целых одна четвертая», а записывается — 5 14.
Что такое десятичная дробь
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,8
- 7,42
- 9,932

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».
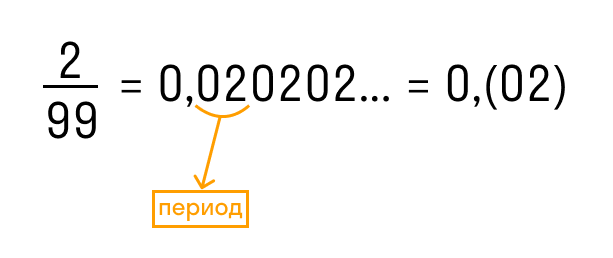
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Как перевести обычную дробь в десятичную
Прежде чем узнать, как от обычной записи перейти к десятичной, вспомним различия двух видов дробей и сформулируем важное правило.
Десятичные дроби — это конструкции вида 0,5; 2,16 и -7,42. А так выглядят эти же числа в форме обыкновенных дробей:

Обыкновенную дробь можно перевести в конечную десятичную дробь только при условии, что её знаменатель можно разложить на простые множители 2 и 5 любое количество раз. Например:
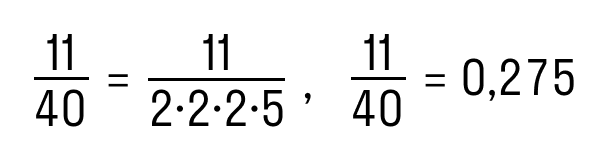
Дробь 11/40 можно преобразовать в конечную десятичную, потому что знаменатель раскладывается на множители 2 и 5.
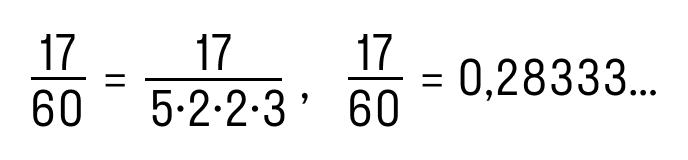
Дробь 17/60 нельзя преобразовать в конечную десятичную дробь, потому что в её знаменателе кроме множителей 2 и 5, есть 3.
А теперь перейдем к самому главному вопросу: рассмотрим несколько алгоритмов перевода обыкновенной дроби в десятичную.
Способ 1. Превращаем знаменатель в 10, 100 или 1000
Чтобы превратить дробь в десятичную, нужно числитель и знаменатель умножить на одно и то же число так, чтобы в знаменателе получилось 10, 100, 1000 и т.д. Но прежде, чем приступать к вычислениям, нужно проверить, можно ли вообще превратить данную дробь в десятичную.
Для примера возьмем дробь 3/20. Ее можно привести в конечную десятичную, потому что её знаменатель раскладывается на множители 2 и 5.
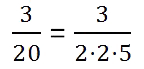
Мы можем получить в нижней части 100: достаточно умножить 20 на 5. Про верхнюю часть тоже не забываем: получаем 15.
Теперь запишем числитель отдельно. Отсчитываем справа столько же знаков, сколько нулей стоит в знаменателе, и ставим запятую. В нашем примере в знаменателе 100 (у него два нуля), значит ставим запятую после отсчета двух знаков и получаем 0,15. Преобразование готово.
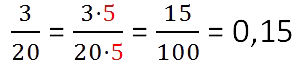
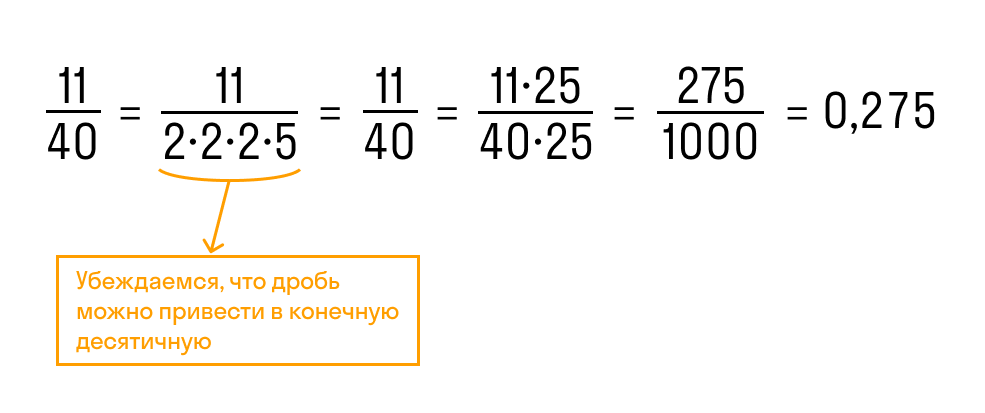
Способ 2. Делим числитель на знаменатель
Чтобы перевести обыкновенную дробь в десятичную, достаточно разделить ее верхнюю часть на нижнюю. Проще всего это сделать, конечно же, на калькуляторе — но на контрольных им пользоваться не разрешают, поэтому учимся по-другому.
Для примера возьмем дробь 78/100. Убедимся, что дробь можно привести в конечную десятичную.
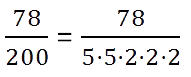
Делим столбиком числитель на знаменатель — преобразование готово:
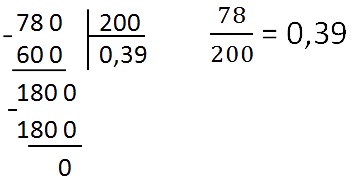
Если при делении уголком стало ясно, что процесс не заканчивается и после запятой выстраиваются повторяющиеся цифры — эту дробь нельзя перевести в конечную десятичную. Ответ можно записать в виде периодической дроби — для этого нужно записать повторяющееся число в скобки, вот так: 1/3 = 0,3333.. = 0,(3).
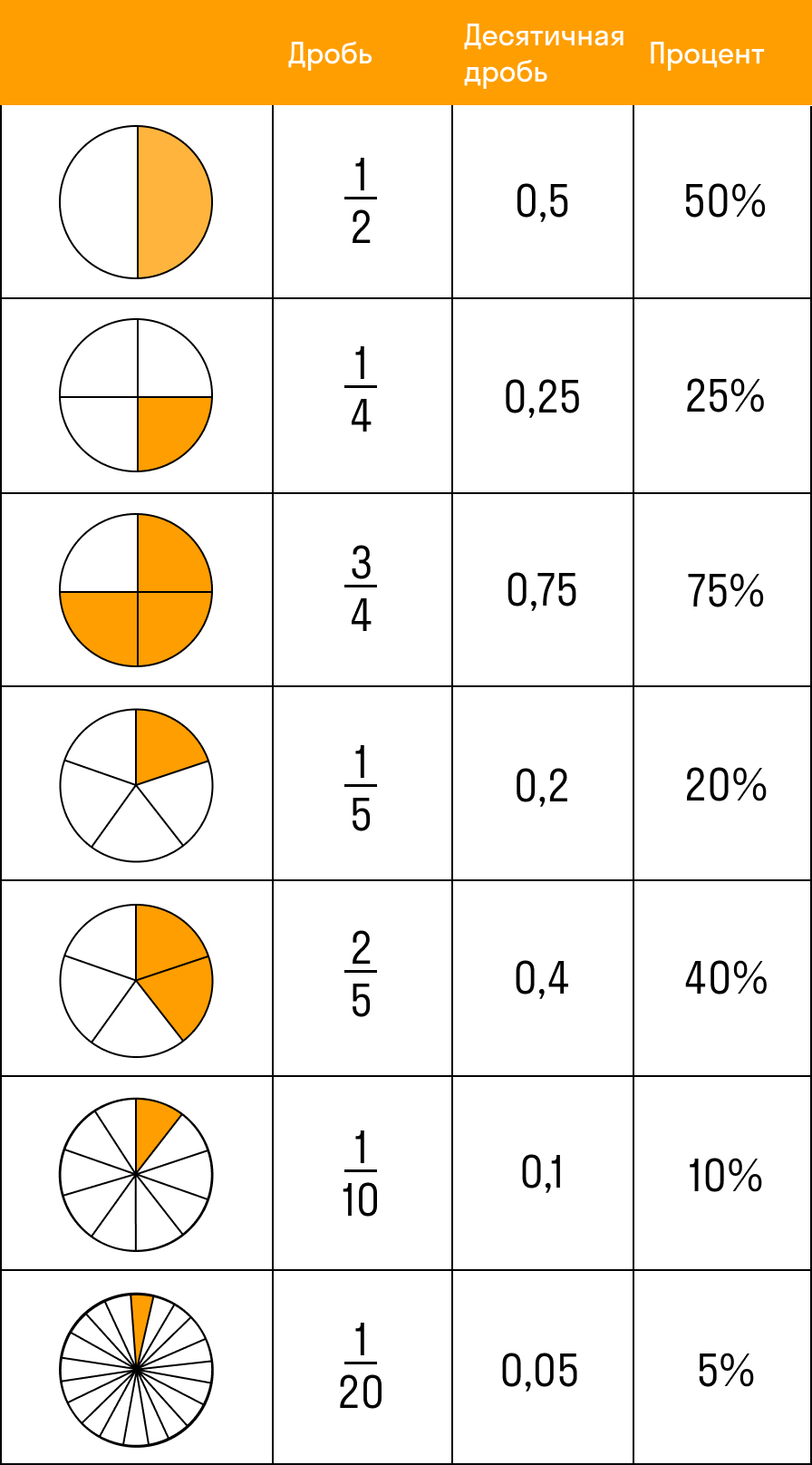
Для удобства мы собрали табличку дробей со знаменателями, которые чаще всего встречаются в заданиях по математике. Скачайте ее на гаджет или распечатайте и храните в учебнике как закладку:
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед. По сути, алгоритм превращения десятичной дроби в обыкновенную противоположен тем, что мы разобрали в предыдущей части. Вот, как это выглядит в обратную сторону:
- Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу:
- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая. При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 6/20, еще раз делим на 2, получаем итоговый ответ 3/10.
- 2,34 = 234/100 = 117/50 = 2 17/50.
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Вот и всё! Эта схема значительно проще и быстрее. Проверим:
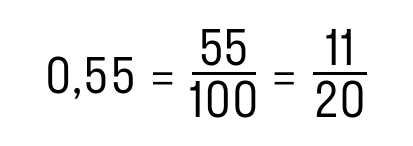
Как видим, в дроби 0,55 после запятой стоит две цифры — 5 и 5. Поэтому n = 2. Если убрать запятую и нули слева, то получим число 55. Переходим ко второму шагу: 10n = 102 = 100, поэтому в знаменателе стоит 100. Остается сократить числитель и знаменатель. Вот и ответ: 11/20.
Как перевести периодическую десятичную дробь в обыкновенную
Любую бесконечную периодическую десятичную дробь можно перевести в обыкновенную. Разберем на примерах.
Если период дроби равен нулю, значит решение будет быстрым. Периодическая дробь с нулевым периодом заменяется на конечную десятичную дробь, а процесс обращения такой дроби сводится к обращению конечной десятичной дроби.
Преобразуем периодическую дробь 1,32(0) в обыкновенную.
Для этого отбросим нули справа и получим конечную десятичную дробь 1,32. Далее следуем алгоритму из предыдущих пунктов:
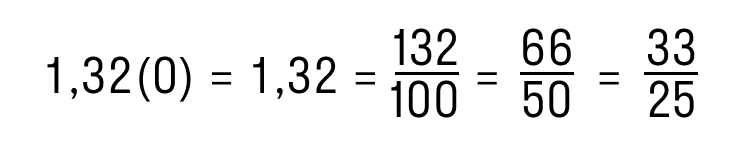
Если период дроби отличен от нуля — рассматриваем периодическую часть как сумму членов геометрический прогрессии, которая убывает. Поясним на примере:
0,(98) = 0,98 + 0,0098 + 0,000098 + 0,00000098 + ..
Для суммы членов бесконечной убывающей геометрической прогрессии есть формула. Если первый член прогрессии равен b, а знаменатель q таков, что 0
Как перевести десятичную дробь в обыкновенную — правило с примерами
Преобразование десятичных дробей в обыкновенные – навык нужный: в жизни нам приходится “переводить” проценты – в рубли, пропорции кулинарных рецептов – в граммы и миллилитры. Но прежде чем познакомиться с парой полезных алгоритмов по “превращению дробей”, вспомним, как сокращаются простые дроби. Нам это пригодится.
Как сокращать дроби
Сократить дробь – значит разделить числитель и знаменатель на одно и то же (максимально возможное!) число. Иногда это число очевидно, иногда – нет.
Например: в дроби оба числа делятся на 5.
Разделим: 5 : 5 = 1, 10 : 5 = 2, следовательно: = ( frac<1> <2>) .
( frac<15> <50>) = ( frac<3> <10>) (разделили все на 5)
( frac<45> <81>) = ( frac<5> <9>) (сократили на 9)
Можно эту процедуру провести в несколько шагов: ( frac<24> <108>) = ( frac<8> <36>) = ( frac<2> <9>) (сначала на 3, потом на 4, а всего на 12).
Важно! Делить числитель и знаменатель надо до тех пор, пока общие делители не закончатся, то есть пока дробь не станет несократимой.
В нашем случае знаменатель всегда будет кратен 10-и: 10, 100, 1000, 10000 и так далее. Значит, общие делители для обоих “этажей” будут те, на которые делятся эти круглые числа: 2, 4, чаще всего – 5, ну и 8, 10, 20, 25, 50 и далее. Если сразу не отыщете нужное, набирайте их постепенно.
Например: как сократить дробь ( frac<750> <1000>) ?
Итого: ( frac<750> <1000>) = ( frac<75> <100>) = ( frac<15> <20>) = ( frac<3> <4>) . Можно было сразу сократить на 250 (10 × 5 × 5 = 250).
Вот теперь можно переходить к главному.
Как превратить десятичную дробь в обычную?
Десятичные дроби (ДД) записываются в строчку: целая часть – до запятой, дробная – после запятой. Например, 3,45 или 0,299.
Обыкновенные (ОД) пишут “в два этажа”: вверху – числитель, внизу – знаменатель. Целую часть – перед дробью. Например: ( frac<4> <5>) , ( frac<25> <70>) , 3 ( frac<2> <7>) .
Есть два основных пути перевода десятичной дроби в обычную и их варианты.
Первый способ – механический
Попробуем 0,05 превратить в ( frac<1> <20>) :
Результат решения: 0,05 = ( frac<5> <100>) = ( frac<1> <20>) .
ДД с целой частью, например 3,075, преобразуем так:
Ход преобразований: 3,075 = ( frac<3075> <1000>) = ( frac<123> <40>) = 3 ( frac<3> <40>) .
- 3 пока не трогаем;
- 0,075 переводим в ОД: ( frac<75><1000>) .
Вся последовательность: 3,075 → 0,075 = ( frac<75> <1000>) = ( frac<3> <40>) → 3 ( frac<3> <40>) .
Второй способ – “на слух”
Этот подход более естественный. Каждый легко запишет под диктовку:
- восемь/девятых – ( frac<8><9>) ;
- одиннадцать/тридцатых – ( frac<11><30>) ;
- сто две/триста семнадцатых – ( frac<102><317>) .
Также можно выразить и десятичную дробь, например, 0,45:
- 0, 45 – это (слушаем!) сорок пять/сотых – ( frac<45><100>) ;
- Теперь сократим на 5: ( frac<45><100>) = ( frac<9><20>) .
В итоге получаем: 0,45 = ( frac<45> <100>) = ( frac<9> <20>) .
Целое, если оно есть, можно “отложить на потом” и вернуть в конце вычислений.
Пусть требуется выразить 14,408 в виде ОД:
Ход решения: 14, 408 = 14 ( frac<408> <1000>) = 14 ( frac<51> <125>) .
Важно! Если перед десятичной дробью был знак “минус”, то он сохраняется и перед обыкновенной дробью. Например: -2,25 = -2= -2.
Еще несколько примеров:
- 1, 08 – одна целая, восемь сотых – 1 ( frac<8><100>) = 1 ( frac<2><25>) (дробную составляющую уменьшили в 4 раза);
- 5,0125 – пять целых, сто двадцать пять/десятитысячных – 5 ( frac<125><1000>) = 5 ( frac<1><80>) (сократили на 125);
- 0,648 – шестьсот сорок восемь тысячных – ( frac<648><1000>) = ( frac<81><125>) (разделили все на 8).
Самое трудное (для тех, кому не все равно)
Что делать, если нужно преобразовать периодическую десятичную дробь? Не вдаваясь в дремучие подробности, познакомимся с надежным алгоритмом.
Итак, требуется выразить 1,(6) в виде ОД.
Пусть обычная дробь – это x, который должен получиться из 1,(6).
x = 1,(6) — умножим обе части равенства на 10
10 x = 16,(6) — вычтем из обеих частей x (или 1,(6) – ведь это одно и то же)
10 x — x = 16,(6) — 1,(6)
Таким образом, 1,(6) = ( frac<15> <9>) .
Попробуйте разделить 15 на 9, и убедитесь, что получится 1,66666 – и так до бесконечности.
Если усложнить: 0,1(23) нужно представить в виде ( frac ) .
x = 0,1(23) — умножим обе части равенства на 1000
1000 x = 123,(23) — вычтем из обеих частей 10 x, другими словами, 1,(23)
Значит — 0,1(23) = ( frac<61> <495>) .
Важно! В этом примере пришлось умножить части уравнения не на 10, а на 1000, вычесть не х, а 10х. Это нужно для того, чтобы легче было искать разность периодов: из 123,(23) удобно вычитать 1,(23). Подходящие коэффициенты придется подбирать в каждом отдельном случае. Но общий ход решения остается постоянным.
Конечно, для проведения подобных вычислений можно обратиться к онлайн-калькулятору. Но, согласитесь, иметь в арсенале знаний оригинальный эффектный прием – особое удовольствие.
Еще больше примеров для полного понимания этой темы смотрите в предложенном видео.
Перевод обыкновенной дроби в десятичную и наоборот
теория по математике числа и вычисления
При решении различных вычислительных заданий требуется произвести перевод десятичной дроби в обыкновенную или наоборот. В частности, в бланках ответов первой части ОГЭ (и ЕГЭ) нельзя записывать обыкновенную дробь, так как поле для этой дроби просто не существует.
Чтобы перевести обыкновенную дробь в конечную десятичную дробь, необходимо разделить числитель дроби на ее знаменатель. Как перевести обыкновенную дробь в конечную десятичную дробь?
Чтобы перевести обыкновенную дробь в конечную десятичную дробь, необходимо разделить числитель дроби на ее знаменатель (устно или в столбик ).
Пример №1. ½ = 0,5 так как 1_2=0,5
Пример №2. ¾ = 0,75 так как 3_4=0,75
Пример №3. Так как 18_25=0,72, то
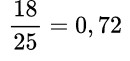
Если дана смешанная дробь, то целая часть уже есть, делим числитель на знаменатель и добавляем в часть после запятой. Или переводим смешанное число в неправильную дробь и делим числитель на знаменатель. Строгого правила для способа выполнения данного действия нет.
Пример №4. 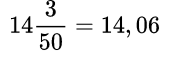
здесь целая часть 14 уже есть, пишем ее и ставим запятую. Затем делим 3 на 50 и получаем 0,06. Приписываем десятичную часть 06 после запятой к числу 14 и получаем 14,06.
Пример №5. 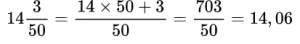
в данном случае сначала перевели смешанное число в неправильную дробь (знаменатель умножается на целую часть и прибавляется числитель — это число записывается в числитель неправильной дроби), а затем разделили числитель 703 на знаменатель 50 и получили 14,06.
Как перевести десятичную дробь (конечную) в обыкновенную?
Чтобы перевести десятичную дробь в обыкновенную, нужно в числитель записать цифры из десятичной части дроби (которые стоят после запятой), а в знаменателе написать столько нулей, сколько цифр получилось в числителе. Затем, по возможности сократить данную дробь.
Пример №6.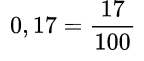
целая часть равна нулю, нуль перед обыкновенной дробью не пишется, 17 записали в числитель, а 100 в знаменатель, так как в числе 17 две цифры, как у сотни два нуля.
Пример №7.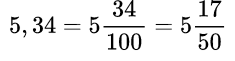
целая часть равна 5, поэтому записали ее перед дробью, 34 пошло в числитель, а знаменатель соответственно равен 100 (по количеству цифр в числе 34). Здесь видно, что получилась сократимая дробь, так как числитель и знаменатель оба делятся на 2. Выполняем сокращение дробной части и получаем новую дробь
Сначала выразим обыкновенную дробь десятичной, разделив 107 на 13, получаем приближенное число 8,23…. Теперь работаем с числовым лучом, на котором видно, что наше число 8,23.. будет располагаться между числами 8 и 9, но ближе к 8, так как оно меньше 8,5; следовательно, это точка А.
pазбирался: Даниил Романович | обсудить разбор | оценить
Одно из чисел 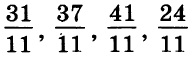 отмечено на прямой точкой.
отмечено на прямой точкой.

Какое это число?

Точка, обозначенная на прямой, лежит между 2 и 3. Т.е. соответствующее ей число больше 1. Это значит, что дробь, которая соответствует этой точке, должна быть неправильной. Но все приведенные в условии дроби неправильные. Чтобы понять, какая из них находится именно на промежутке (2; 3), необходимо выделить их целые части. Та из дробей, у которой целая часть окажется равной 2, и есть искомый результат.
Итак, выделяем целые части:
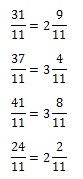
Целую часть, равную 2, имеют две дроби – 1-я и 4-я. Но посмотрим внимательно на прямую. Обозначенная на ней точка находится близко к делению 3. Проанализируем в этом контексте подходящие нам дроби. У первой недостает всего 2/11, чтобы она стала равной 3, между тем как четвертая лишь на 2/11 удалена от деления 2. Следовательно, правильным ответом в данном случае является дробь 31/11. Она соответствует варианту ответа 2.
pазбирался: Даниил Романович | обсудить разбор | оценить
На координатной прямой отмечена точка А:
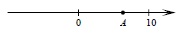
Известно, что она соответствует одному из четырёх указанных ниже чисел. Какому из чисел соответствует точка А?
Подход к решению в данной задаче сводится к визуальной оценки имеющихся вариантов на координатной прямой, для этого необходимо предварительно перевести варианты ответов к примерному десятичному виду.
Оцениваем 181/16 — можно поделить 181 на 16, тогда получим 11,3125. Это явно выходит за указанный диапазон, поэтому данный вариант нам не подходит.
Оцениваем √37 — самое близкое значение, из которого вычисляется квадратный корень — это 36, значит √37 — это 6 и что-то еще, что вычислять нам не обязательно. Данное значение нам подходит, так как лежит чуть правее середины отрезка 0-10, как и точка А.
Посмотрим на вариант 0,6 — это явно меньше единицы, а точка А, как мы уже выяснили, лежит в диапазоне 5-10. Данный вариант нам не подойдет.
Вариант с ответом 4 также не подойдет по вышеуказанной причине.
pазбирался: Даниил Романович | обсудить разбор | оценить
Какое из следующих чисел заключено между числами 8/3 и 11/4 ?
В задании данного типа необходимо выполнить деление 8 на 3 и 11 на 4, то есть перевести дробь из обыкновенного вида в десятичный. Сами дроби могут не иметь представления в десятичном виде, однако в нашем случае достаточно выполнить деление но второго знака после запятой, так как в ответе приведены числа до первого знака после запятой. Итак, выполняем деление:
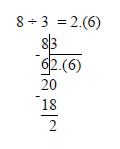
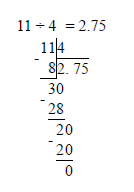
Получаем значения 2,666.. или 2,(6) и 2,75. Смотрим на варианты ответов и выбираем, соответственно, первый, так как 2,7 находится между 2,(6) и 2,75.
pазбирался: Даниил Романович | обсудить разбор | оценить
К данному заданию, как и к большинству заданий 1 модуля Алгебры, подход к решению заключается в переводе дроби от одного вида к другому. В нашем случае это переход от обыкновенной дроби к десятичной.
Переводим ¼ из обыкновенной дроби в десятичную. Делим 1 на 4, получаем 0,25. Затем переписываем выражение с использованием только десятичных дробей и вычисляем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.
Вычислим значение знаменателя:
Можно произвести вычисления в столбик , тогда получим:
Либо перевести дробь к простому виду:
4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4
Последний случай предпочтительней, так как для дальнейшей операции — деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:
9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )
9 и 45 можно сократить на 9:
( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8
pазбирался: Даниил Романович | обсудить разбор | оценить
Перевод десятичной дроби в обыкновенную
Любую десятичную дробь можно представить в виде обыкновенной дроби. Для этого надо просто записать её со знаменателем.
Главное правило в переводе десятичной дроби в обыкновенную — как читается десятичная дробь, так и пишется обыкновенная. Например:
2,3 — две целых три десятых.
Так как дробь имеет целую часть, то перевести её мы можем или в смешанное число или в неправильную дробь:
| 2,3 | = | 2 | 3 | = | 23 | . |
| 10 | 10 |
Если у десятичной дроби нет целой части, например:
0,75 — ноль целых семьдесят пять сотых,
то её можно сразу перевести в правильную обыкновенную дробь и, если нужно (по необходимости), сократить:
| 0,75 | = | 75 | = | 3 | . |
| 100 | 4 |
Перевод обыкновенной дроби в десятичную
Не любую обыкновенную дробь можно перевести в десятичную, так как чтобы записать обыкновенную дробь в виде десятичной, надо привести её к знаменателю, представляющему собой единицу с одним или несколькими нулями, например: 10, 100, 1000 и т. д. Если разложить такой знаменатель на простые множители, то получится одинаковое количество двоек и пятёрок:
100 = 10 · 10 = 2 · 5 · 2 · 5;
1000 = 10 · 10 · 10 = 2 · 5 · 2 · 5 · 2 · 5.
Никаких других простых множителей эти разложения не содержат, следовательно:
Обыкновенную дробь можно представить в виде десятичной только в том случае, если её знаменатель не содержит никаких других множителей, кроме 2 и 5.
При разложении её знаменателя на простые множители получается произведение 2 · 2:
| 3 | = | 3 | . |
| 4 | 2 · 2 |
Если домножить его на две пятёрки, чтобы уравнять количество пятёрок с двойками, то получится один из нужных знаменателей — 100. Чтобы получить дробь равную данной, то числитель тоже надо будет умножить на произведение двух пятёрок:
| 3 | = | 3 · 5 · 5 | = | 75 | = | 0,75. |
| 4 | 2 · 2 · 5 · 5 | 100 |
Рассмотрим ещё одну дробь:
| 5 | . |
| 14 |
При разложении её знаменателя на простые множители получается произведение 2 · 7, содержащее число 7:
| 5 | = | 5 | . |
| 14 | 2 · 7 |
Множитель 7 будет присутствовать в знаменателе, на какие бы целые числа его ни умножали, поэтому произведение, содержащее только двойки и пятёрки никогда не получится. Значит данную дробь нельзя привести ни к одному из нужных знаменателей: 10, 100, 1000 и так далее. То есть её нельзя представить в виде десятичной.
Обыкновенную несократимую дробь нельзя представить в виде десятичной, если её знаменатель содержит хотя бы один простой множитель, отличный от 2 и 5.
Обратите внимание, что в правиле написано только о несократимых дробях, потому что некоторые дроби после сокращения, можно представить в виде десятичных. Рассмотрим две дроби:
| 5 | и | 7 | . |
| 14 | 14 |
Первая дробь является несократимой и, как мы уже выяснили, её нельзя представить в виде десятичной. Во второй дроби числитель и знаменатель можно сократить на 7, то есть на тот простой множитель, который мешает в первой дроби:
| 7 | = | 7 : 7 | = | 1 | . |
| 14 | 14 : 7 | 2 |
Теперь осталось только умножить оба члена дроби на 5, чтобы получить 10 в знаменателе, и можно будет переводить дробь в десятичную:
Способ перевести десятичную дробь в обыкновенную: правила
При изучении математики важно не только знать, как перевести десятичную дробь в обыкновенную, но и уметь применять полученные знания на практике. Обучают этой науке в четвертом классе средней школы. Преобразование выражений позволяет упрощать различные задачи, делая решение простым и понятным. Сама операция несложная, но требует понимания смысла использования дробных чисел. Лишь в этом случае действие можно будет довести до автоматизма и выполнять устно.

Виды дробей
Дробь — это число, в состав которого входит одна доля или несколько её частей, поделенных на равные части. По сути, это отношение двух значений. Обыкновенное дробное выражение записывают с помощью натуральных чисел, разделённых горизонтальной чертой. Называется она винкулумом. В литературе можно встретить и другой тип записи с наклонной чертой (солидус).
Верхнее число, или стоящее слева от черты, называют числителем или делимым, а нижнее — знаменателем (делителем). Что такое дробь, удобнее всего объяснить на примере. Пусть на столе стоит тарелка, на которой лежит пирог. Он один и целый. Можно взять нож и разделить его на шесть равных частей.
По сути, количество пирога не изменится, поэтому, с математической точки зрения, на тарелке будет всё так же находиться целый пирог. Если с неё взять два куска, то целостность нарушится. Записывают это действие с помощью дроби: 2/6. То есть внизу указывают число, обозначающее, на сколько поделили пирог, а сверху — сколько кусков забрали.
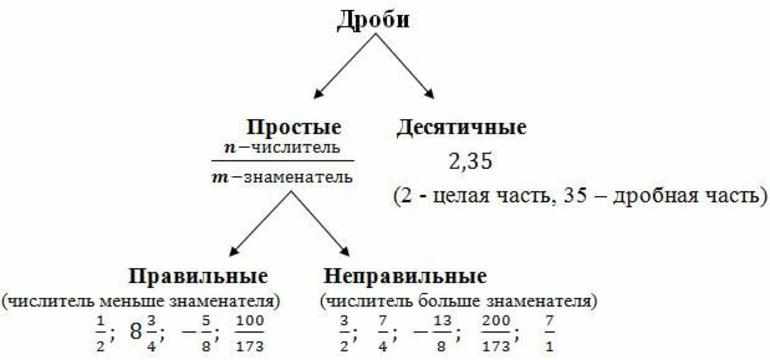
Дробь — это число, обозначающее часть целого предмета. При этом дробное отношение всегда будет меньше единицы. Существующие отношения принято разделять на следующие виды:
- Правильные — отношения, в которых числитель меньше знаменателя.
- Неправильные — дроби, где делимое по величине превышает делитель.
- Смешанные — состоящие из суммы натурального и дробного числа.
- Десятичные — в знаменателе которых стоит натуральное число с размерностью кратной десяти.
- Составные — состоящие из нескольких черт дроби.
С дробными отношениями можно выполнять любые математические действия. Их складывают, вычитают, умножают, возводят в степень. Замечательным свойством дробей есть возможность их преобразования из одного вида в другой. Например, можно перевести обычную дробь в десятичную, неправильную — в смешанную. При этом операции возможны как в одну, так и другую сторону.
Проводимые операции, кроме получения периодической дроби, можно выполнять и в обратную сторону. Остаток при делении должен всегда быть меньше делителя. Поэтому, если при действии получается ноль, деление прекращается, а если остаток — бесконечная периодическое отношение.
Чаще всего для того, чтобы преобразовать простую дробь в десятичную, необходимо выполнить три шага:

- Сократить выражение, требующее преобразования.
- Разделить удобным способом числитель на знаменатель. В зависимости от величины значений, стоящих в числителе и знаменателе, это можно сделать столбиком или в уме. Если при делении остаток выходит отличным от нуля, то поставить запятую и продолжить искать частное.
- Записать найденный результат с использованием запятой.
Нужно отметить, что алгоритм, объясняющий правило того, как перевести обыкновенную дробь в десятичную, подходит лишь для случаев, когда знаменатель раскладывается на множители пять и два. В иных случая получится периодическое десятичное число.
Решение примеров
Порой теоретическая информация довольно трудно воспринимается без применения её на практике. Поэтому крайне важно не только посмотреть, как делает преобразование учитель, но и самостоятельно выполнить перевод. Обычно хватает трех-четырех примеров для каждого типа преобразований, чтобы закрепить материал и освоить практическое применение.
Существуют определённые сборники заданий, предназначенные для самостоятельного решения учащимися. Вот некоторые наиболее интересные примеры из них:

- Преобразовать: 1/1000, 34/10, 78954/10, 186/100, 959/10000. Алгоритм действия определяется правилом отсчитывания запятой. В задании три нуля, но в числителе только один знак. Поэтому на недостающих местах следует поставить нули. Отсюда следует что 1/1000 = 0,001. По аналогии нужно решать и следующие примеры. В итоге должно получиться: 34/10 = 3,4, 78954/10 = 7895,4, 186/100 = 1,86, 959/10000 = 0,0959.
- Записать выражения в обыкновенном виде: 0,59, 34,78, 0,00078, 767,009. В соответствии с правилом в числителе записывают исходное число, а в знаменатель ставят единицу: 0,59 = 0,59/1. Для избавления от запятой делимое и делитель умножают на сто, так как по условию после запятой стоит два знака: (0,59 * 100) / (1 * 100) = 59/100. Аналогично решают и оставшиеся примеры: 34,78 = 34,78/1 = 34,78 * 100/ 100 = 3478/100, 0,00078 = 78/100000 = 39/50000, 767,009 = 767 + 0,009= 767 9/1000.
- Перевести выражения в десятичный вид: 5/2, ¼, 34/81, 456/1245, 1245/456. Преобразование таких примеров можно выполнить путём деления числителя на знаменатель для нахождения частного. В первом случае пять нужно разделить на два. Используя деление в столбик, можно опередить, что целым будет число два (2 * 2 = 4). Так как в остатке получается единица, то в частном ставят запятую, а к остатку дописывают ноль. То есть, 5/2 = 2,5. Таким же образом переводят и другие примеры: ¼ = 0,25, 34/81 = 0,420, 456/1245 = 0,366, 1245/456 = 2,73.
Эти задания затрагивают преобразование как в одну, так и в другую сторону. После первичного перевода не стоит забывать об упрощении полученного результата. Его нужно делать всегда, чтобы в дальнейшем при решении сложных задач последующие действия становились проще.
Использование онлайн-конвертера
Десятичные дроби могут состоять из довольно больших чисел. Поэтому не всегда их можно быстро преобразовать. При этом любая невнимательность может привести к ошибке, что повлечёт неверный как промежуточный, так и итоговый результат. В таких случаях есть резон использовать так называемый конвертер дробей.
Это интернет-сервис, предоставляющий услуги по автоматическому преобразованию дробей из одного вида в другой. Для того чтобы воспользоваться его возможностями, пользователю даже необязательно понимать принцип перевода выражений. От него требуется лишь ввести исходные данные в предлагаемую форму и нажать кнопку «Рассчитать».
Таких математических сервисов в интернете довольно много. Русскоязычные конвертеры не требуют регистрации и указания каких-либо персональных данных. При этом свои услуги они предоставляют бесплатно. Согласно отзывам пользователей, можно выделить следующие онлайн-калькуляторы:

- 0oq,
- onlinemschool,
- naobumium,
- allcalc,
- webmath.
Нужно отметить, что приведенные сайты являются настоящими математическими комбайнами-решателями. Они умеют не только конвертировать дроби, но и выполнять с ними любые действия. Например, складывать, делить, умножать, извлекать корень и возводить в степень. Кроме этого, на их страницах содержится теоретический материал и подробное описание решений.





